Математика 2 семестр. Решение Имеем однородную систему линейных уравнений, решим ее методом Гаусса
 Скачать 31.82 Kb. Скачать 31.82 Kb.
|
|
2 семестр 1. Найти собственные значения и собственные векторы матрицы 1.1. 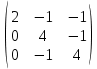 Решение: Имеем однородную систему линейных уравнений, решим ее методом Гаусса: 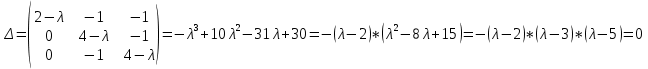 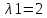 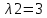 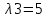 Имеем однородную систему линейных уравнений, решим ее методом Гаусса: 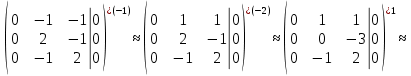 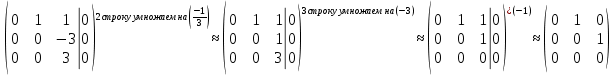 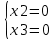 Из уравнения 2 системы найдем переменную Х3=0 Из уравнения 1 системы найдем переменную Х2=0 Ответ: X1=X1 X2=0 X3=0 Общее решение: Х= 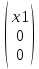 1.2. 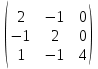 Решение: 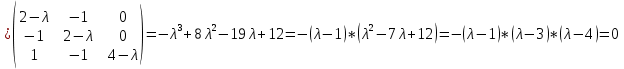 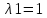 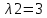 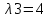 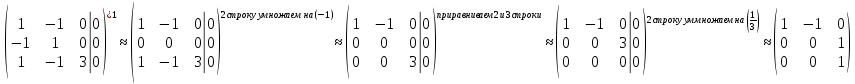 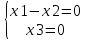 Из уравнения 2 системы найдем переменную Х3=0 Из уравнения 1 системы найдем переменную Х1=Х2 Ответ: X1=X2 X2=X2 X3=0 Общее решение: Х= 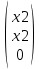 2. Исследовать знакопостоянство выражения 2.1. 5x2-6xy+2y2 2.2. 4x2+3xy-5y2 2.3. 4x2+2xy-4y2 Решение: 2.1. 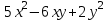 . .Запишем матрицу квадратичной формы: 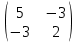 . Вычислим определители: . Вычислим определители: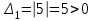 , , 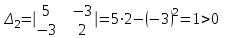 . В соответствии с критерием Сильвестра квадратичная форма знакоположительная, следовательно, выражение принимает неотрицательные значения. . В соответствии с критерием Сильвестра квадратичная форма знакоположительная, следовательно, выражение принимает неотрицательные значения.2.2. 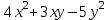 . .Запишем матрицу квадратичной формы: 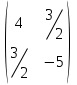 . Вычислим определители: . Вычислим определители: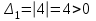 , , 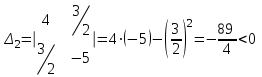 . В соответствии с критерием Сильвестра квадратичная форма не является знакоопределенной, следовательно, выражение принимает значения любого знака. . В соответствии с критерием Сильвестра квадратичная форма не является знакоопределенной, следовательно, выражение принимает значения любого знака.2.3. 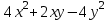 . .Запишем матрицу квадратичной формы: 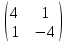 . Вычислим определители: . Вычислим определители: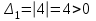 , , 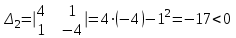 . . В соответствии с критерием Сильвестра квадратичная форма не является знакоопределенной, следовательно, выражение принимает значения любого знака. Ответ: 2.1. квадратичная форма знакоположительная, следовательно, выражение принимает неотрицательные значения; 2.2. квадратичная форма не является знакоопределенной, следовательно, выражение принимает значения любого знака; 2.3. квадратичная форма не является знакоопределенной, следовательно, выражение принимает значения любого знака. 3. Составить уравнение прямой, проходящей через точку пересечения прямых 2x-3y+5=0 и 3x+y-7=0 перпендикулярно к прямой y=2x Решение: 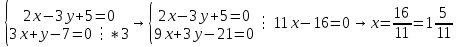 Найдем y=7-3x из второго уравнения: 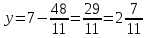 Следовательно, 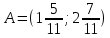 Уравнение прямой, проходящей через точку А – 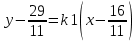 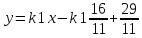 Найдем k1: 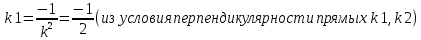 Искомое уравнение прямой принимает вид: 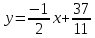 Ответ: уравнение прямой, проходящей через точку пересечения прямых 2x-3y+5=0 и 3x+y-7=0 перпендикулярно к прямой y=2x выглядит следующим образом: 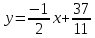 Тестовые задания
|