Геометрия решение контрольной работы Иващенко Иван Андреевич. Решение Итак, дана окружность с центром в точке и точка, не лежащая на этой окружности (см рис. 1). Нужно построить прямую, проходящую через точку и касающуюся окружности.

• Название: Решение Итак, дана окружность с центром в точке и точка, не лежащая на этой окружности (см рис. 1). Нужно построить прямую, проходящую через точку и касающуюся окружности.
• Дата: 07.11.2020
• Размер: 131.39 Kb.
• Имя файла: Геометрия решение контрольной работы Иващенко Иван Андреевич.docx
• Тип: Анализ; #148621

Вариант 3.

1 . Постройте треугольник по стороне, медиане, проведённой к данной стороне и прилетающему к этой стороне углу.


Дано:



Построение:


2. Докажите любой признак равенства треугольников.

1 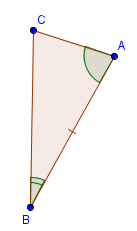)  по стороне и прилежащим к ней углам

Доказательство:

Пусть АВС и А1В1С1 – два треугольника, у которых АВ равно А1В1, угол А равен углу А1, и угол В равен углу В1. Докажем, что они равны.

Наложим треугольник ABC (либо симметричный ему) на треугольник A1B1C1 так, чтобы AB совпало с A1B1. Так как ∠ВАС =∠В1А1С1 и ∠АВС=∠А1В1С1, то луч АС совпадёт с А1С1, а ВС совпадёт с В1С1. Отсюда следует, что вершина C совпадёт с С1. Значит, треугольник А1В1С1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Теорема доказана.

Вариант 4.

1. 
   Постройте касательную к данной окружности, проходящую через заданную точку.
   

Решение:

Итак, дана окружность с центром в точке   и точка  , не лежащая на этой окружности (см. рис. 1). Нужно построить прямую, проходящую через точку   и касающуюся окружности. Используйте тот факт, что радиус, опущенный в точку касания, перпендикулярен касательной.



Рис. 1. Иллюстрация к задаче 1

Первый этап. Анализ

Анализ не требует точных построений. И рассуждения начинаются с конца: «предположим, мы уже построили касательную».

Обозначим точку касания 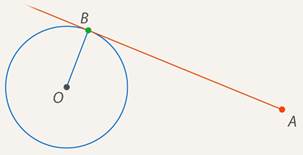 . Проведем радиус   (см. рис. 2).



Рис. 2. Иллюстрация к задаче 1

Как мы уже сказали, свойством касательной к окружности является тот факт, что касательная перпендикулярна радиусу, который проведен в точку касания:



Продолжим 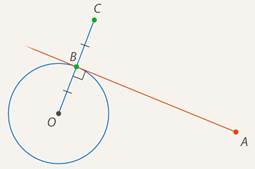  и отметим на нем точку   так, чтобы   (см. рис. 3).



Рис. 3. Иллюстрация к задаче 1

Полученный большой треугольник 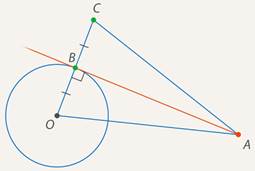  является равнобедренным, т. к. у него высота   является медианой (см. рис. 4).



Рис. 4. Иллюстрация к задаче 1

В этом треугольнике мы знаем все три стороны:





Треугольник по трем сторонам строить мы умеем. Похоже, мы решили задачу.

Переходим к следующим этапам. Обратите внимание, что нашей целью было свести задачу к одной из тех, которые мы умеем решать. В данном случае нам удалось свести к задаче о построении треугольника по трем сторонам.

Второй этап. Построение

Начертим окружность с центром в точке 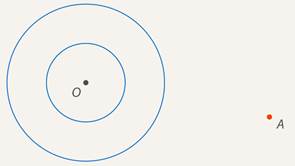  и точку   вне окружности. Построим еще одну окружность с центром в точке   с радиусом в два раза большим, чем первая (см. рис. 5).

 

Рис. 5. Иллюстрация к задаче 1

Получить радиус в два раза больший данного можно разными способами. Например, можно использовать диаметр первой окружности. Далее проведем окружность с центром в точке 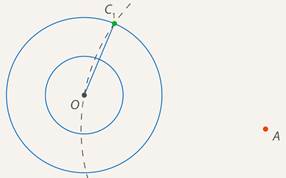  и радиусом  . Пересечение окружностей дают точку  . Проведем отрезок   (см. рис. 6).



Рис. 6. Иллюстрация к задаче 1

Точку пересечения 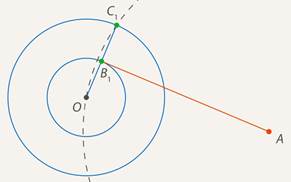  соединим с точкой  ,   – искомая касательная (см. рис. 7).



Рис. 7. Иллюстрация к задаче 1

Третий этап. Доказательство

После построения необходимо доказать, что мы построили именно то, что нас просили. Доказательство обычно почти повторяет первый пункт – анализ, но требует четкой записи. Итак, докажем, что в самом деле касательная.

Рассмотрим треугольник 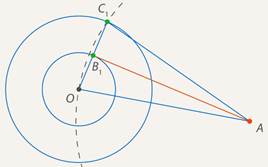  (см. рис. 8).



Рис. 8. Иллюстрация к задаче 1

Т. к. 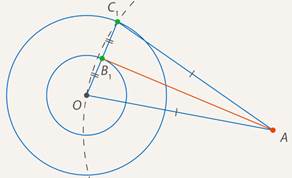  и   лежат на одной окружности с центром в  , то  , т. е. треугольник равнобедренный.

Т. к.   лежит на окружности в два раза большего радиуса, чем  , то   – середина отрезка  :   (см. рис. 9).



Рис. 9. Иллюстрация к задаче 1

Значит,   – медиана  . Но т. к. треугольник равнобедренный, то она является и высотой. Т. к.   перпендикулярен радиусу  , то   – касательная.

Доказано.

Четвертый этап. Исследование

Здесь изучается вопрос: всегда ли в рамках заданных условий решение у задачи есть и сколько их. По нашим анализам и построениям мы видим, что решения всегда есть и их два. Через точку 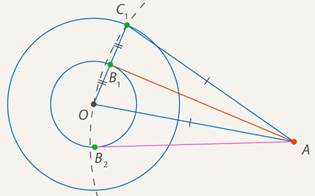  можно провести не одну касательную, а две. Вторая точка касания на нашем чертеже – это   (см. рис. 10).



Рис. 10. Иллюстрация к задаче 1

Задача решена.

2. 
   Докажите любой из признаков подобия треугольников.
   

Теорема 1 (первый признак):

Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Доказательство

Дано:  АВС и  А₁В₁С₁,  А =  А₁,  В =  В₁

Доказать:  АВС А₁В₁С₁

Доказательство: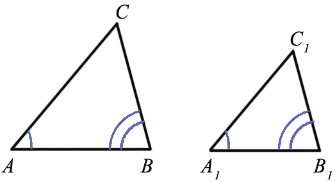



По теореме о сумме углов треугольника  А + В + С = 180⁰ и  А₁+ В₁+ С₁= 180⁰, другими словами,  С = 180⁰ -  А - В  и  С₁= 180⁰ -  А₁- В₁, и, значит,   С =  С₁. Таким образом, углы треугольника АВС соответственно равны углам треугольника А₁В₁С₁.

Докажем, что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Так как 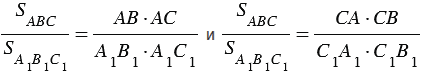 А =  А₁ и  С =  С₁, то,





Так как 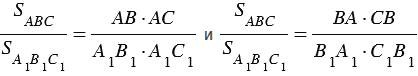 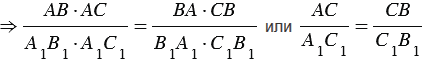А =  А₁ и  В =  В₁, то





Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Теорема доказана.