Решение. Момент встречи точек Тогда. Подставим числовые значения Значит
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
105. Две материальные точки в момент t=0 начинают двигаться по прямой линии согласно уравнениям x1=A1+A2t+A3t4, x2=B1+B2t+B3t4, где A1 = 50 м, A2 = 2 м/с, A3 = -3 м/с4, B1 = 42 м, B2 = 10 м/с, B3 = -3 м/с4. Найти скорости и ускорения этих точек в момент их встречи.
Тогда, Подставим числовые значения: Значит, Скорость – первая производная от перемещения. Значит, Ускорение – первая производная от скорости. Значит, Тогда, Проверка размерности: Получаем, Ответ. 116. Расположенный горизонтально сплошной цилиндр может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра 12 кг. На цилиндр намотали шнур к концу которого привязали гирю массой 1 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?
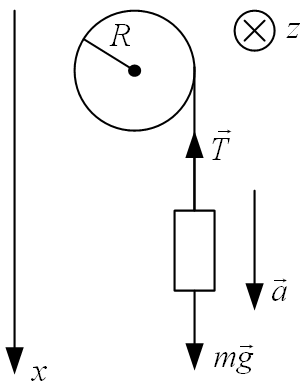 Уравнение вращательного движения маховика имеет вид: Ось Тогда, в проекции на ось Момент силы натяжения нити равен: Угловое ускорение определяется по формуле: Значит,  . .С другой стороны момент инерции цилиндра равен: 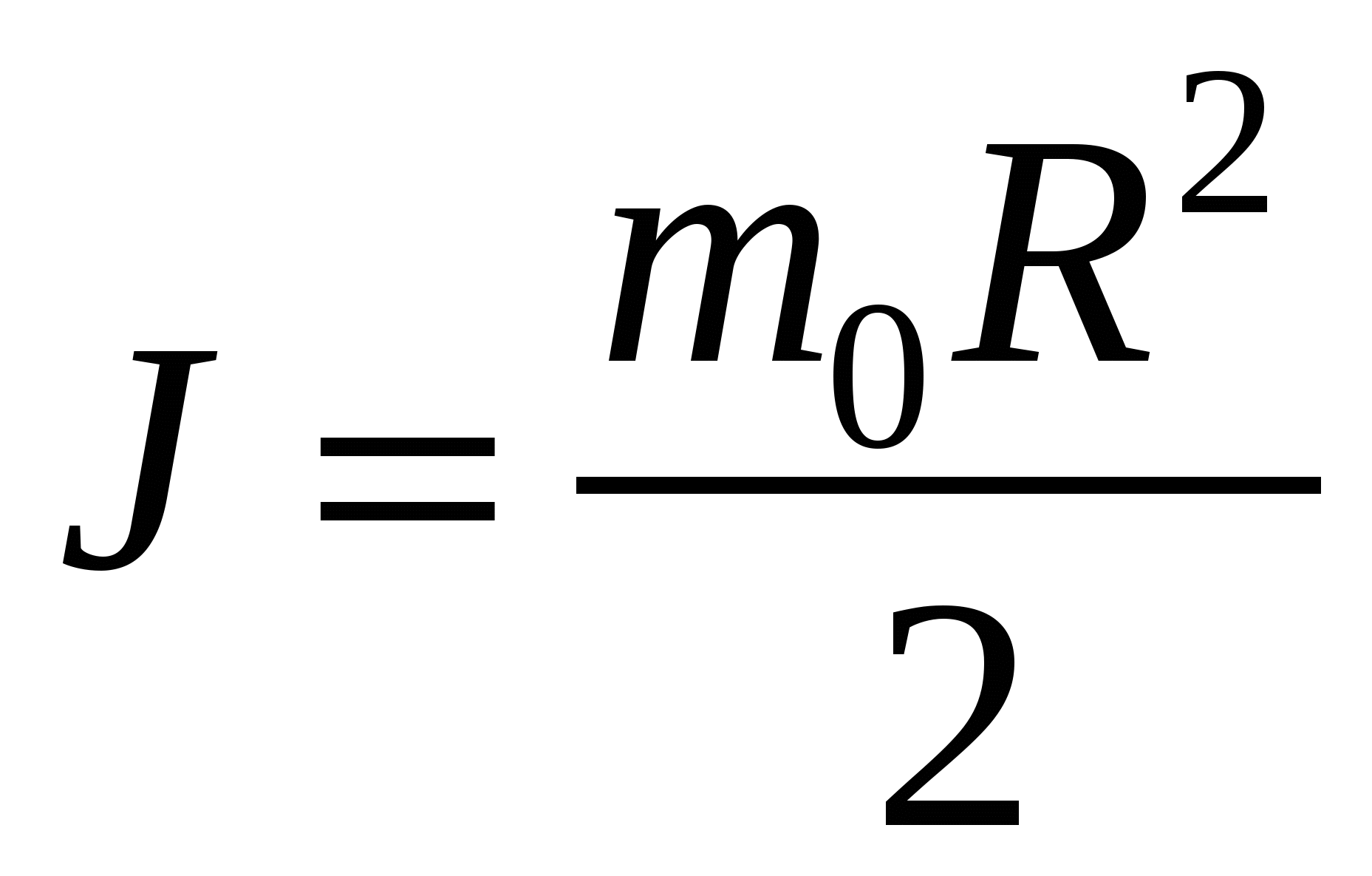 . .Значит,  . .Для груза по второму закону Ньютона для тела массой m имеем: В проекции на ось x имеем: Тогда,  . .Тогда,  . .Проверка размерности:  , , . .Получаем, Ответ. 125. На круглой вращающейся скамейке стоит человек и держит в руках стержень, расположенный вертикально, по оси вращения скамейки. Скамейка с человеком вращается с угловой скоростью 1 рад/с. С какой угловой скоростью будет вращаться скамейка с человеком, если повернуть стержень так, чтобы он принял горизонтальное положение? Суммарный момент инерции человека и скамейки равен 6 кг·м2. Длина стержня 2,4 м, а его масса равна 8 кг.
 Система «человек-скамейка-стержень» замкнута. Момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени: По закону сохранения момента импульса в проекции на ось y имеем: где Значит,  . .Проверка размерности:  . .Получаем,  . . Ответ. 134. На какую высоту над поверхностью Земли поднимается ракета, пущенная вертикально вверх, если начальная скорость ракеты будет равна первой космической скорости?
По закону сохранения энергии имеем: Так как кинетическая энергия 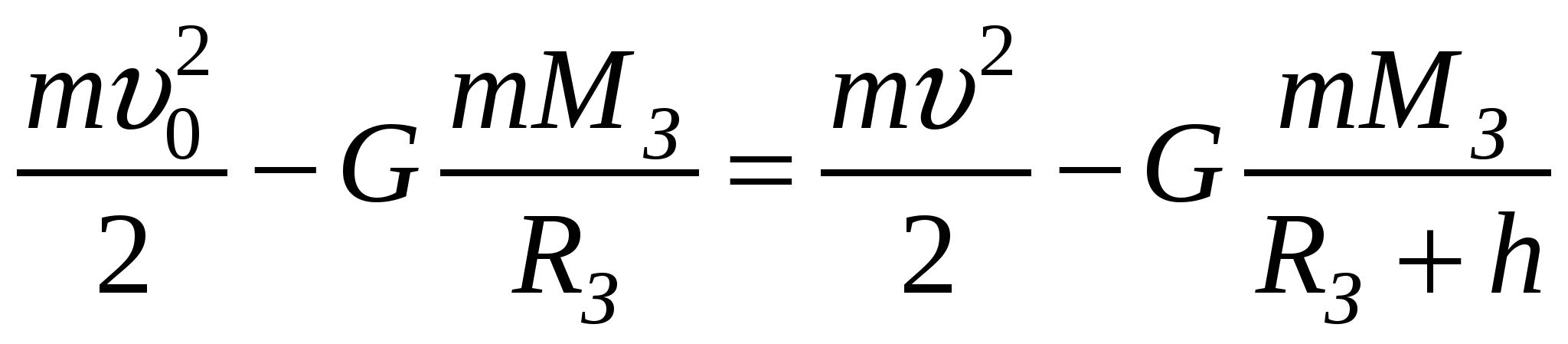 , где , где Так как конечная скорость равна нулю  . .Так как 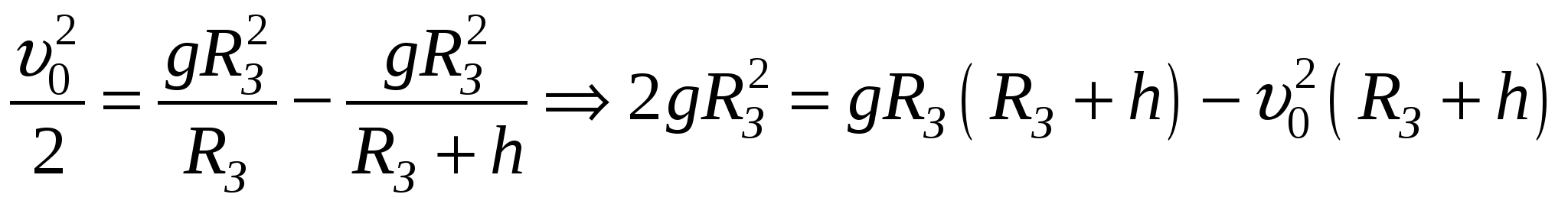 . .Откуда, 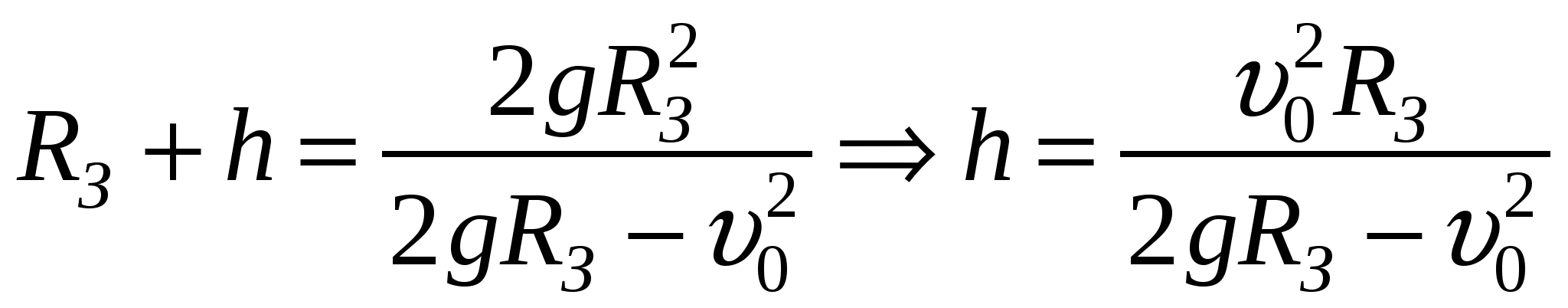 . . Проверка размерности:  . .Получаем,  . .Ответ. 149. Определить частоту колебаний физического маятника, состоящего из обруча массой 400 г и радиусом 30 см, внутри которого укреплен однородный диск массой 200 г и диаметром 10 см. Маятник совершает колебания относительно горизонтальной оси, проходящей через точку О.
 Период колебаний физического маятника равен: 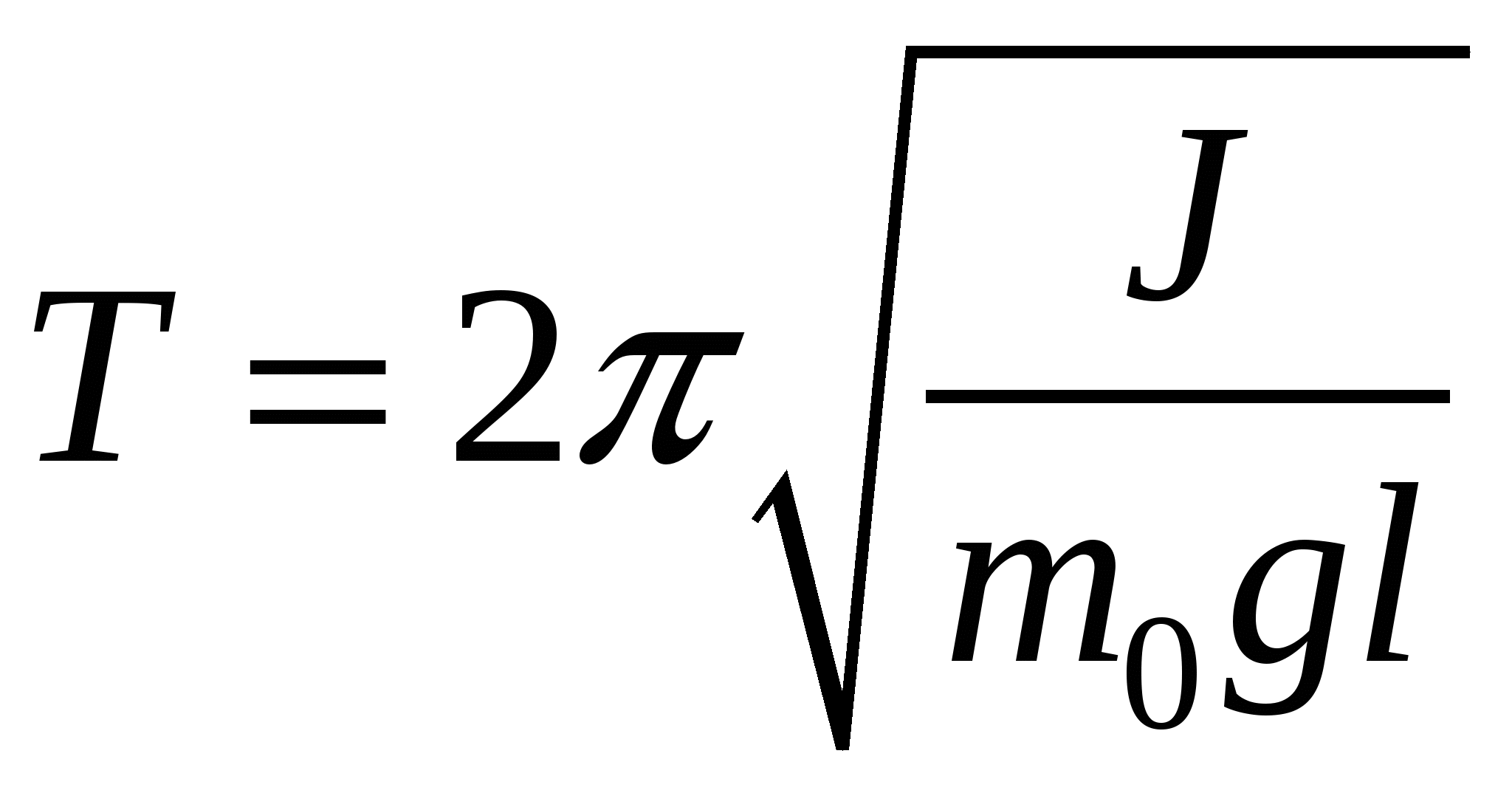 , , где  - момент инерции диска относительно точки О, - момент инерции диска относительно точки О, Значит,  . .Расстояние центра масс маятника от оси колебаний равно:  . .Тогда,  . .Значит, 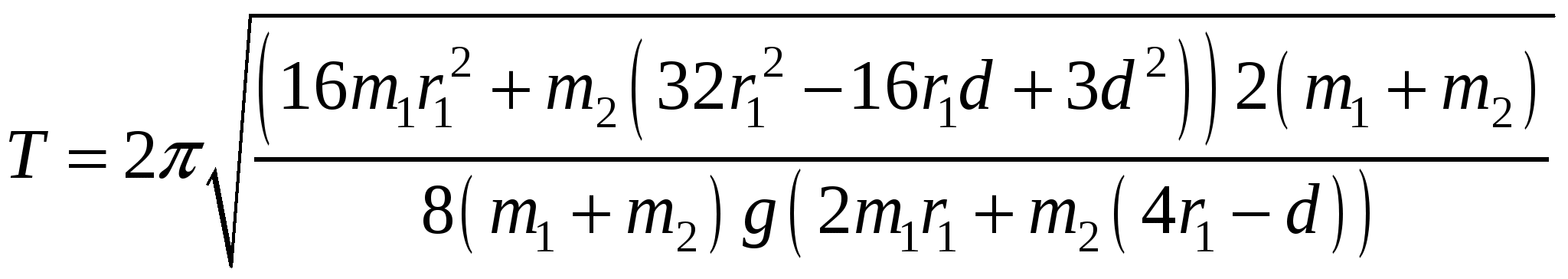 . .Тогда,  . .Частота равна: Тогда,  . .Проверка размерности:  . .Получаем,  . .Ответ. 154. Однородный шар массой 5 кг может вращаться без трения вокруг вертикальной оси, проходящей через его центр. На «экватор» шара намотана невесомая нерастяжимая нить, другой конец которой перекинут через цилиндрический блок массой 1 кг и привязан к грузу массой 10 кг. Какую скорость будет иметь груз, опустившись на расстояние 1 м? Трением в осях пренебречь. В начальный момент груз покоился.
 Уравнение вращательного движения шара имеет вид: где Ось Тогда, в проекции на ось Момент инерции шара определяется по формуле: Момент силы натяжения нити равен: Угловое ускорение равно: Значит, Уравнение вращательного движения блока имеет вид: Ось Тогда, в проекции на ось Момент инерции блока определяется по формуле: Моменты силы натяжения нитей равны: Угловое ускорение равно: Значит, Теперь рассмотри тело массой По второму закону Ньютона имеем: В проекции на ось y имеем: Тогда, 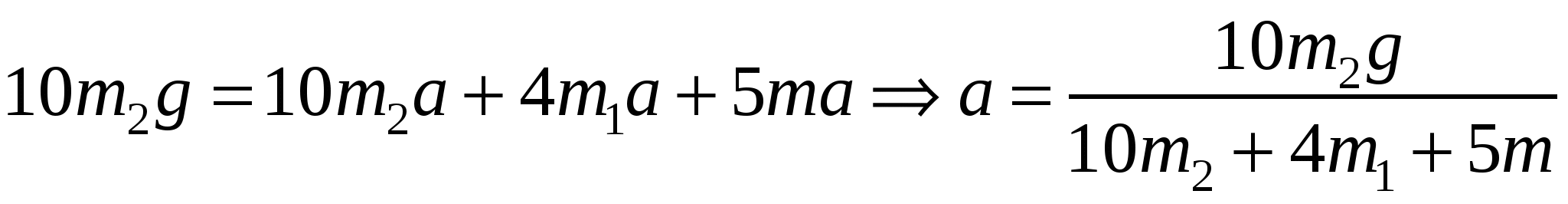 . .Так как движение тела Так как скорость в начальный момент равна нулю, то имеем: Тогда,  . .Значит,  . .Проверка размерности:  . .Получаем,  . .Ответ. 168. Кинетическая энергия поступательного движения молекул азота, находящегося в баллоне объемом 0,02 м3, равна 5 кДж, а средняя квадратичная скорость его молекул равна 2·103 м/с. Найти: 1) массу азота в баллоне; 2) давление, при котором находится азот.
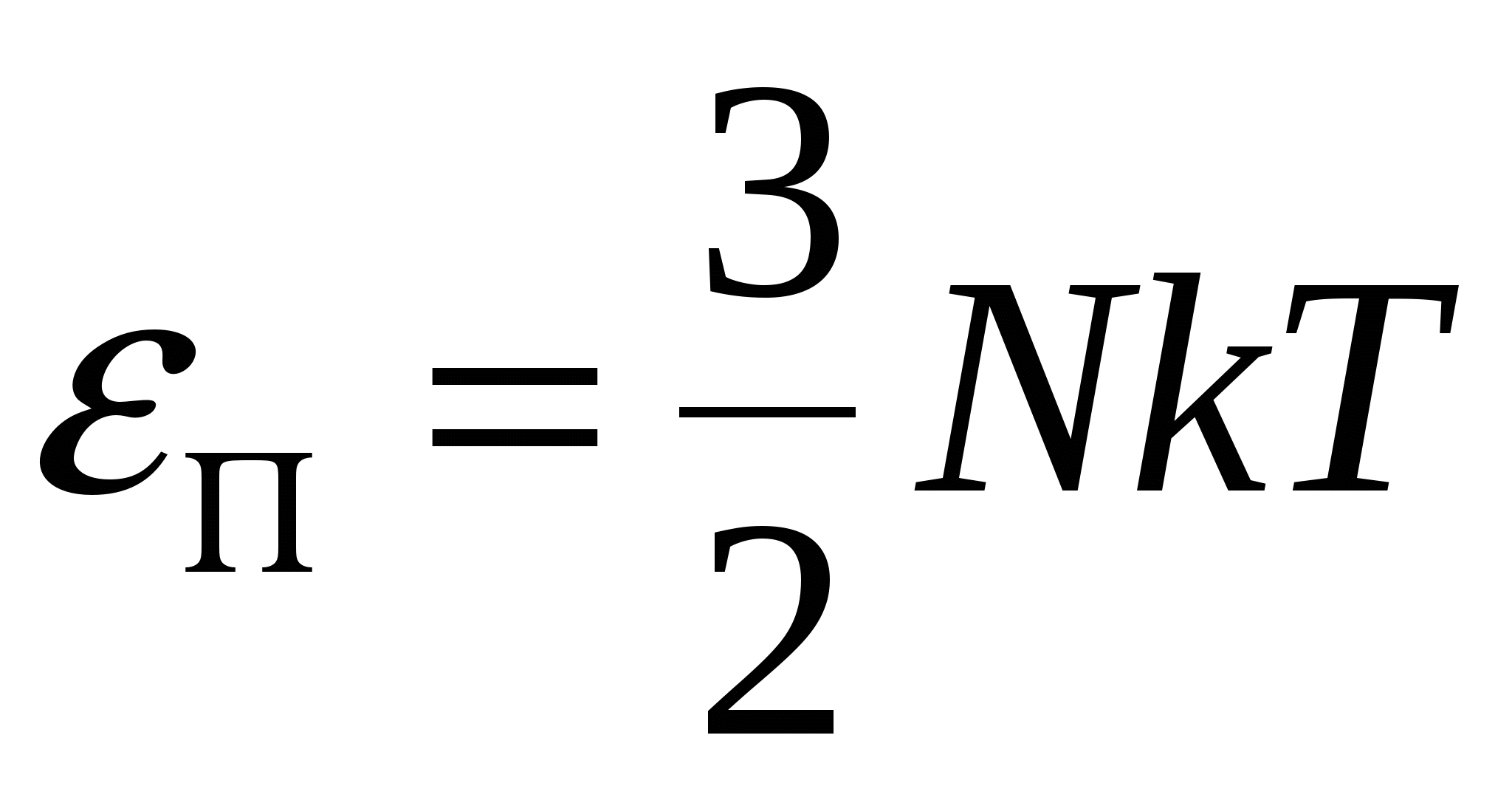 , где , где Количество вещества определятся по формулам:  , где , где  - молярная масса азота, - молярная масса азота, Тогда,  . .Значит,  . .Известно, что Значит,  . .Средняя квадратичная скорость равна:  . . Значит,  . .Тогда,  . .По уравнению Менделеева-Клапейрона имеем:  . .Тогда,  . .Проверка размерности:  , ,  . .Получаем, 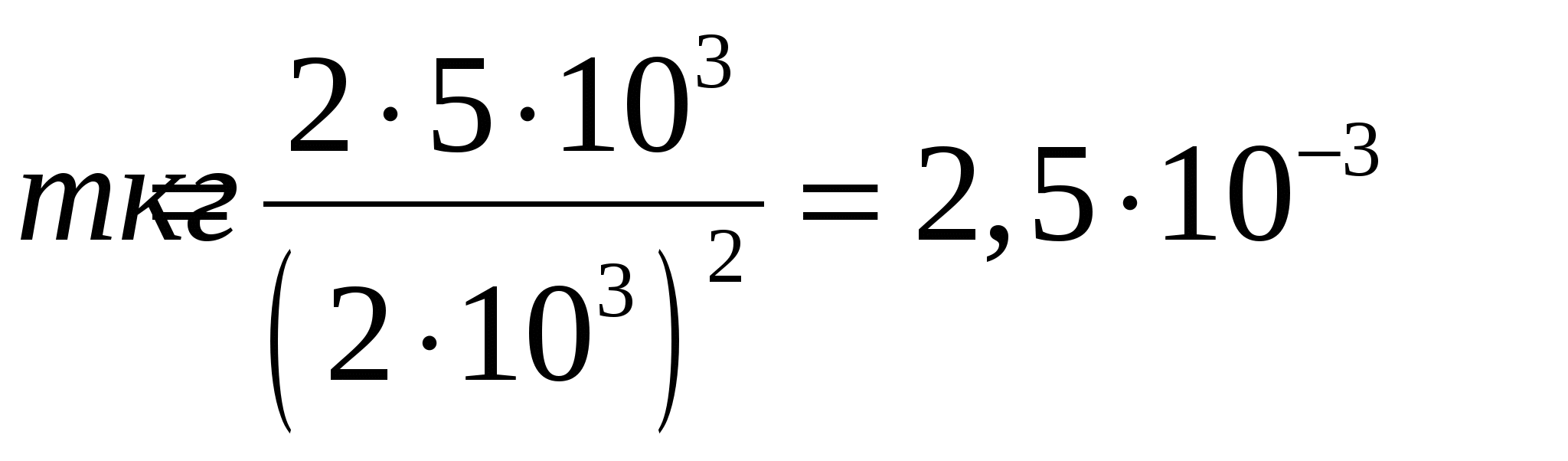 , , Ответ. 174. На какой высоте плотность газа составляет 50% от плотности его на уровне моря? Температуру считать постоянной и равной 0ºС. Задачу решить для: 1) воздуха; 2) водорода.
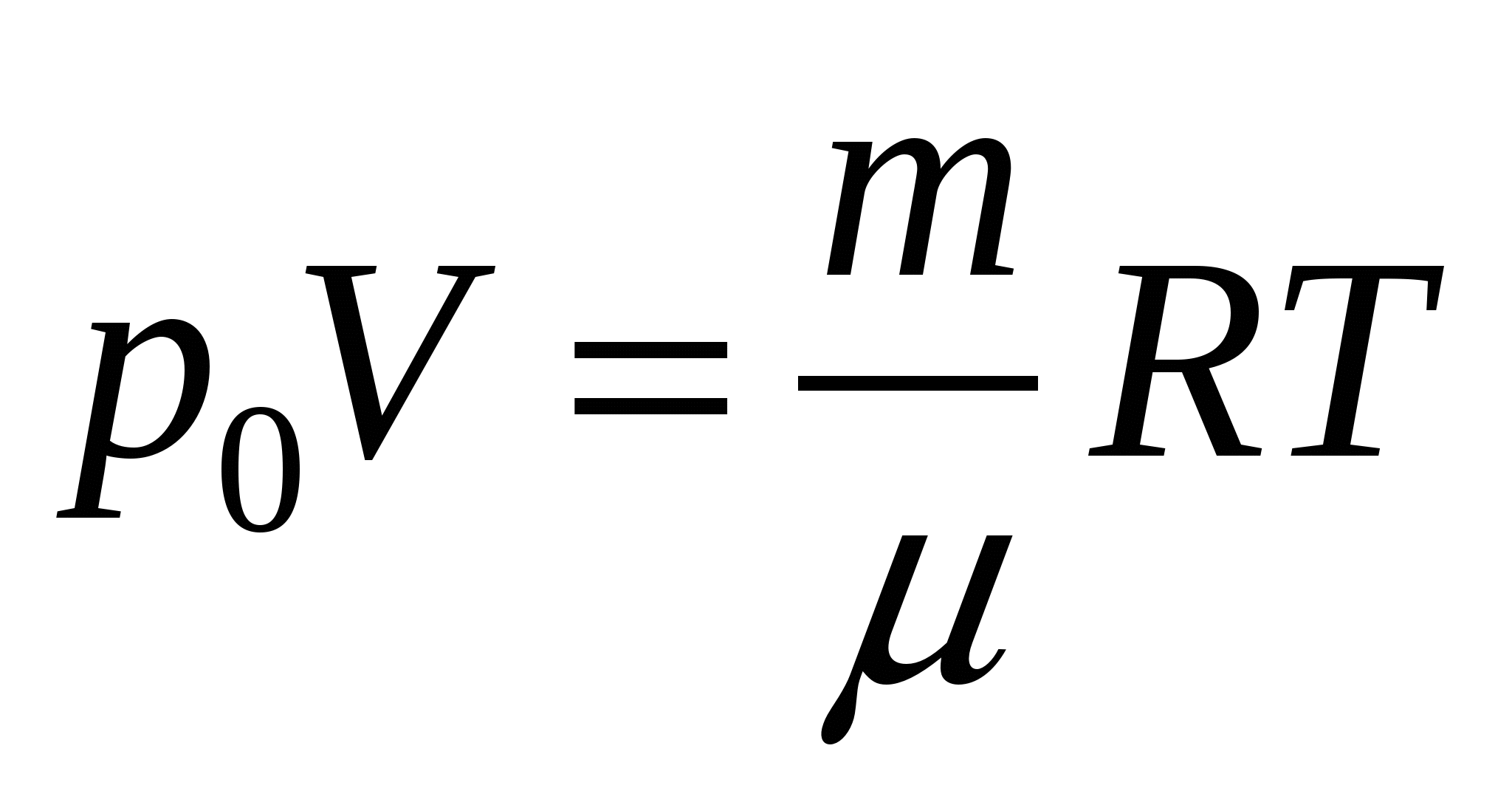 , , где Так как плотность равна По барометрической формуле имеем: 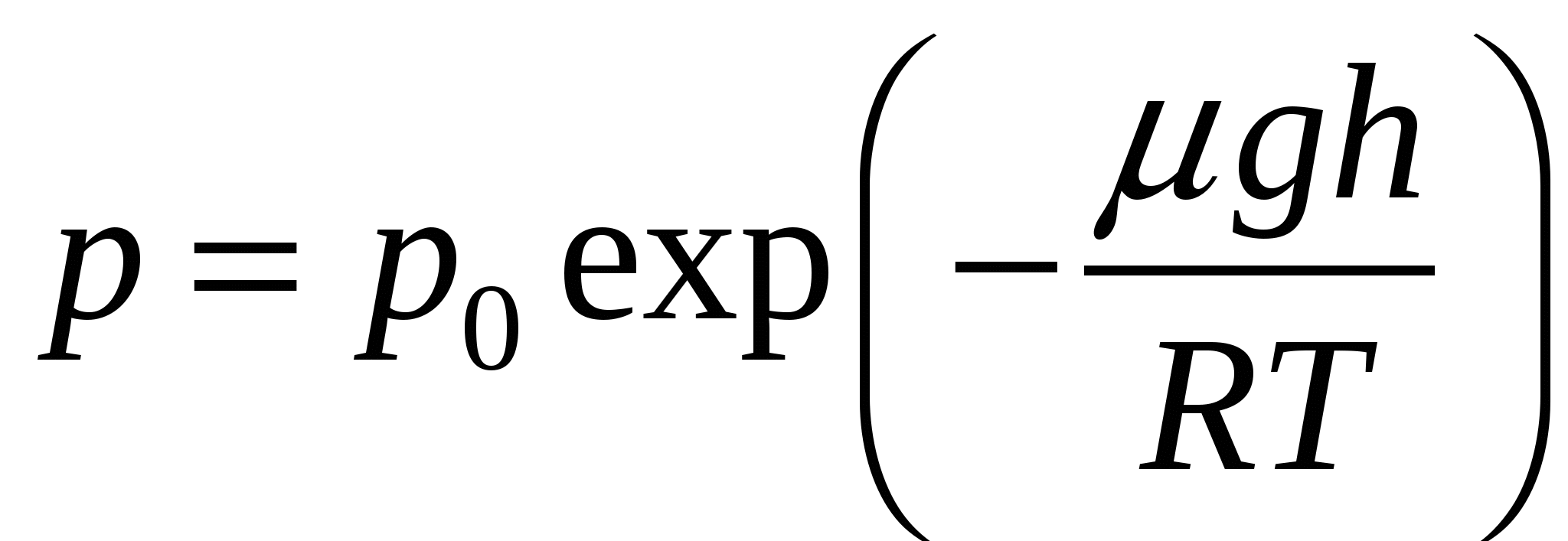 . . Тогда,  . .Значит,  . .Тогда, для воздуха и азота имеем: 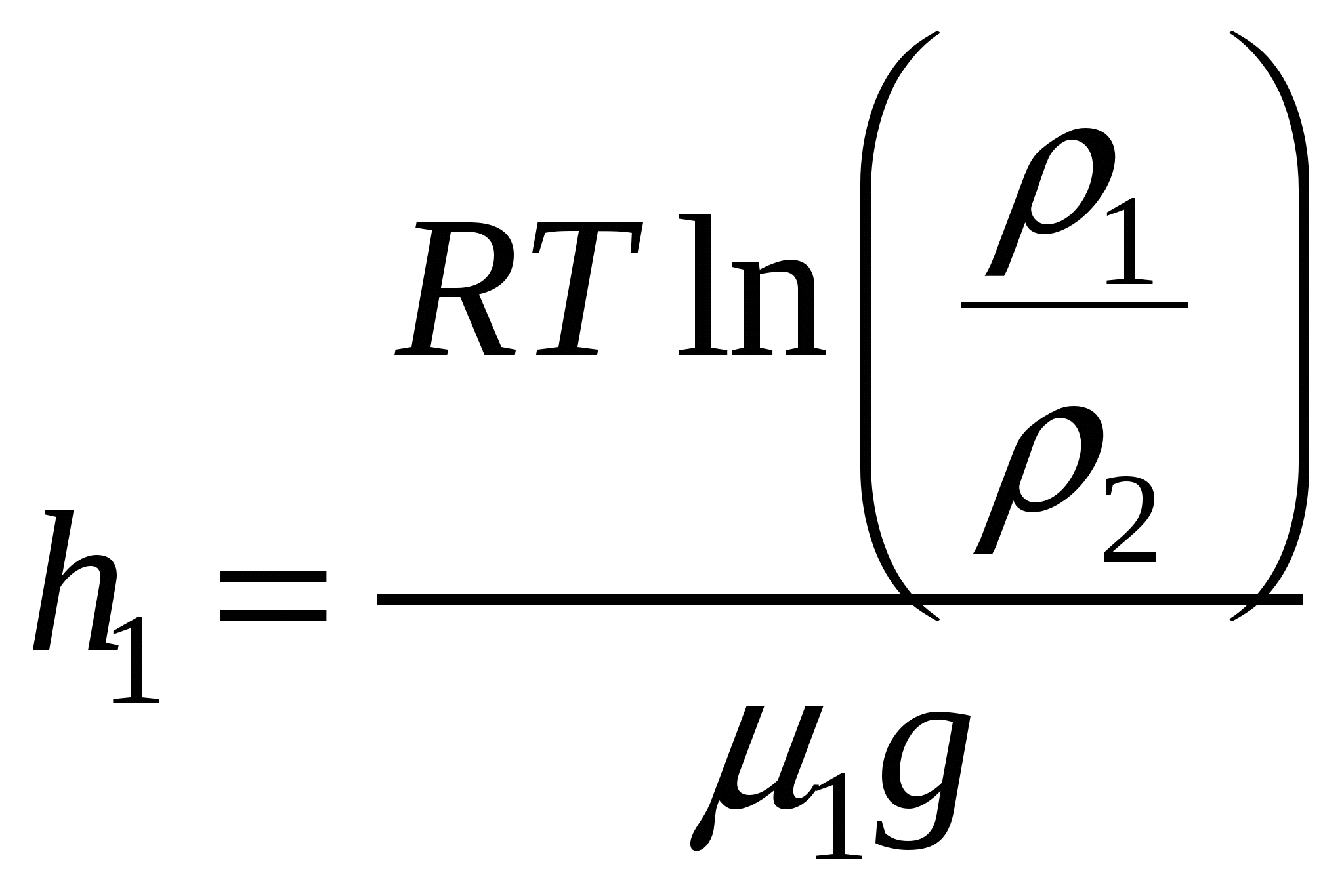 , ,  , ,где Проверка размерности:  . .Получаем,  , ,  . .Ответ. |
