Решение На первое подвешенное тело действуют сила тяжести и сила натяжения нити, на второе тело соответственно действуют сила тяжести и сила натяжения нити

• Название: Решение На первое подвешенное тело действуют сила тяжести и сила натяжения нити, на второе тело соответственно действуют сила тяжести и сила натяжения нити
• Дата: 29.12.2021
• Размер: 0.69 Mb.
• Имя файла: Fizika_2.doc
• Тип: Решение; #321439

1.020. В установке известны масса однородного сплошного цилиндра М = 1 кг, его радиус R = 20 см и массы тел m₁=2 кг и m₂=1 кг. Скольжения нити и трения в оси цилиндра нет. Определить ускорения всех тел.

Дано:









Найти:



Решение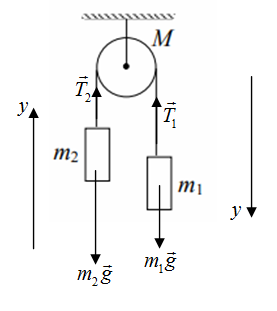


На первое подвешенное тело  действуют сила тяжести и сила натяжения нити , на второе тело соответственно действуют сила тяжести и сила натяжения нити .

Запишем второй закон Ньютона для подвешенного тела (тела массой ):

+ = (1)

Запишем уравнение (1) в проекциях на выбранную ось :

(2)

Запишем второй закон Ньютона для подвешенного тела (тела массой ):

(3)

Запишем уравнение (3) в проекциях на выбранную ось :

(4)

Разность сил натяжения создает вращательный момент. По определению момент силы можем выразить так:

(5)

Где – радиус диска.

Запишем второй закон динамики для вращательного движения диска:

(6)

Где – момент инерции цилиндра; – угловое ускорение цилиндра.

Запишем связь между угловым и линейным ускорениями:

(7)

Момент инерции диска равен:

(8)

– масса диска.

Подставим (7) и (8) в (6):

(9)

Из (5) и (9) запишем:



_Или


(10)

Из (2) находим:
(11)

Из (4) находим:

(12)

Подставим (11) и (12) в (10):








_{Отсюда:}





Подставим данные в последнее выражение:



Ответ: _.

1.030. Тело массой m₁=2 кг движется навстречу второму телу массой m₂=1,5 кг и соударяется с ним. Скорости тел непосредственно перед ударом были v₁=1 м/c и v₂=2 м/c. Определить расстояние, пройденное телами после удара, если коэффициент трения μ=0,05. Соударение считать неупругим.

Дано:











Найти:



Решение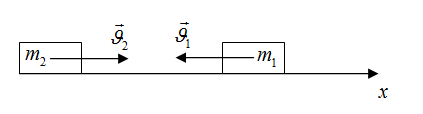



По закону сохранения импульса, учитывая, что удар неупругий, можем записать:

(1)

Где – масса первого тела; – масса второго тела; – скорость первого тела до удара; – скорость второго тела до удара; – общая скорость обеих тел после удара.

Запишем уравнение (1) в проекции на ось :



Отсюда:

(2)



После удара два тела будут двигаться как единое целое. При этом на них будут действовать сила тяжести , сила трения и сила реакции опоры . Исходя из второго закона Ньютона, можем записать:

(3)

Где – ускорение тел.

Запишем последнее уравнение в проекции на ось :



или:

(4)

Здесь учли, что поскольку движение равнозамедленное, то .

Запишем выражение для перемещения тела при равнозамедленном движении:



Где – начальная скорость тела; – конечная скорость тела. Учитывая, что тело остановилось, то его конечная скорость равна нулю: . Тогда последнее выражение примет вид:

(5)

Запишем выражение (3) в проекции на ось :



Отсюда:



По определению сила трения равна:



Из двух последних выражений можем записать:

(6)

Из выражений (4) и (6) можем записать:



Отсюда:

(7)

Подставим (2) и (7) в (5):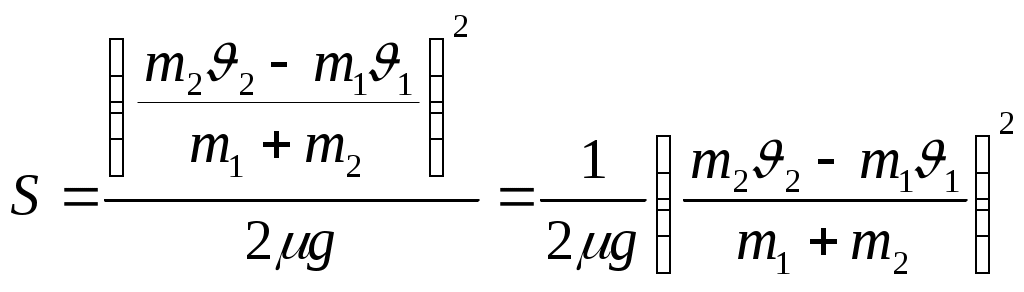





Подставим данные в последнее выражение:



Ответ: .

1.050. Колебания материальной точки происходят согласно уравнению где А=8 см, с^-1 . В момент, когда возвращающая сила в первый раз достигла значения -5 мН, потенциальная энергия точки стала равной 100 мкДж. Найти этот момент времени и соответствующую ему фазу.

Дано:











Найти:

– ?

– ?
Решение

Уравнение колебаний имеет вид:

(1)

Где – амплитуда колебаний; – циклическая частота; – начальная фаза.

Сравнивая уравнение (1) с исходным уравнением находим, что начальная фаза . Поэтому уравнение (1) можем переписать так:

(2)

Взяв первую производную смещения по времени, найдем скорость колеблющейся точки:

(3)

Для нахождения ускорения возьмем производную от скорости по времени:

(4)
Возвращающую силу найдем исходя из второго закона Ньютона:

(5)
Подставим (4) в (5):

(6)

Кинетическая энергия колеблющейся точки равна:

(7)

Где – масса точки.

Подставим (3) в (7):

(8)

Полная энергия материальной точки, совершающей колебания равна:

(9)

Тогда потенциальная энергия будет равна:

(10)

Подставим (9) и (8) в (10):

(11)

Отсюда:

(12)

Подставим (12) в (6):
(13)

Отсюда:


(14)

Отсюда:

(15)
Подставим данные в (14) и (15):





Ответ: ; .
1.070. Баллон вместимостью V=20 л заполнен азотом при температуре T=400 К. Когда часть газа израсходовали, давление в баллоне понизилось на Δp=200 кПа. Определить массу m израсходованного газа. Процесс считать изотермическим.

Дано:











Найти:

– ?

Решение
Запишем уравнение Менделеева-Клайперона сначала для состояния 1, а потом для состояния 2, учитывая, что :

(1)

(2)

Где – молярная масса газа; и – соответственно начальная и конечная масса газа в сосуде; и – соответственно начальное и конечное давление газа; – универсальная газовая постоянная; – объем газа; – температура газа.

Из уравнения (1) находим:

(3)

Из уравнения (2) находим:

(4)

Из выражений (3) и (4) можем записать:



(5)

Подставим данные в (5):



Ответ:
1.090. Определить количество теплоты Q, которое надо сообщить кислороду объемом V=50 л при его изохорном нагревании, чтобы давление газа повысилось на Δp = 0,5 МПа.

Дано:







Найти:



Решение

Согласно первому началу термодинамики, количество теплоты , полученное газом, расходуется на изменение внутренней энергии ΔU и совершение газом работы А против внешних сил:

(1)

При изохорическом процессе работа равна нулю . В этом случае уравнение (1) запишется так:

₍₂₎

Известно, что изменение внутренней энергии для любого термодинамического процесса равно:

Изменение внутренней энергии равно:

(3)

где – число степеней свободы; – молярная масса газа; – масса газа; – универсальная газовая постоянная; – начальная температура газа; – конечная температура газа.

Запишем уравнение Менделеева-Клайперона:

(4)

Где – молярная масса газа; – масса газа; – давление газа; – универсальная газовая постоянная; – объем газа; – температура газа.
Запишем уравнение (4) сначала для состояния 1, а потом для состояния 2, учитывая, что :
(5)

(6)
Из уравнений (5) и (6) можем записать:



Или

(7)
Учитывая (7), выражение (3) можем записать так:

(8)

Учитывая (7), выражение (2) можем записать так:

(9)

Подставим данные в (9), учитывая, что для двухатомной молекулы, какой является молекула кислорода i=5. 



Ответ: .
1.100. Удельная теплоемкость некоторого двухатомного газа с_р=14,4 кДж/(кгК). Определить молярную массу μ этого газа.

Дано:





Найти:



Решение

Удельная теплоемкость газа при постоянном давлении определяется формулой:



где R =8,31 Дж/(моль⋅К) газовая постоянная;  – молярная масса газа; где  i – число степеней свободы.

Отсюда:



Подставим данные в последнее выражение, учитывая, что для двухатомного газа :



Ответ: (водород).

1.110. Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причем наибольшее давление газа в два раза больше наименьшего, а наибольший объем в четыре раза больше наименьшего. Определить термический КПД η цикла.

Дано:





Найти:



Решение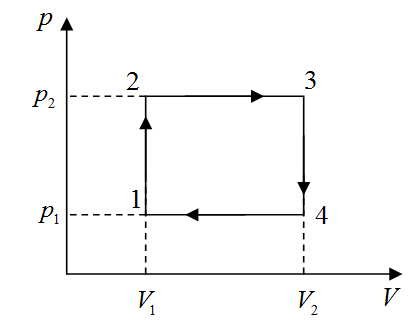



По определению КПД цикла равно:

(1)

Где – совершенная газом за цикл работа; – количество теплоты, полученной за цикл от нагревателя.

Работа численно равна площади внутри графика циклического процесса (площади прямоугольника 1234):

(2)

Газ получал тепло на участках и . Тогда можем записать:

(3)

Согласно первому началу термодинамики, количество теплоты Q, полученное газом, расходуется на изменение внутренней энергии ΔUи совершение газом работы А против внешних сил:

(4)

Переход – изохорный процесс. Для изохорного процесса , соответственно

(5)

Запишем уравнение Менделеева – Клапейрона для двух состояний газа:





Где – количество молей газа; – универсальная газовая постоянная; и – соответственно начальная и конечная температура газа.

Из последних двух уравнений можем записать:



Изменение внутренней энергии равно:

(6)

где i – число степеней свободы. Для одноатомного газа i=3.

Тогда можем записать:

(7)

Переход – изобарный процесс. Тогда для этого перехода ( ), исходя из выражения (4), можем записать:

(8)

Запишем уравнение Менделеева – Клапейрона для двух состояний газа:





Из последних двух уравнений можем записать:

(9)

Из выражений (7) и (8) можем записать:

(10)

Работа для изобарного процесса равна:

(11)

Подставим (9) и (10) в (8):



Учитывая, что согласно условию задачи, , , последнее выражение примет вид:

(12)

Подставим (7) и (12) в (3):

(13)

Подставим (2) и (13) в (1):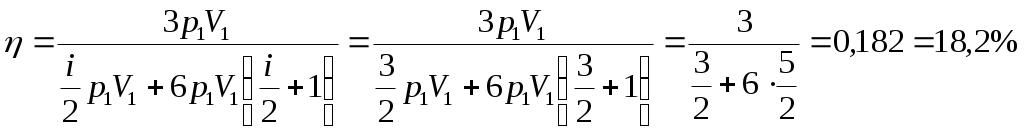





Ответ: .

1.130. Найти скорость течения углекислого газа по трубе, если известно, что за время t=30 мин через поперечное сечение трубы протекает масса газа m=0,51 кг. Плотность газа 7,5 кг/м³. Диаметр трубы 2 см.

Дано:









Найти:



Решение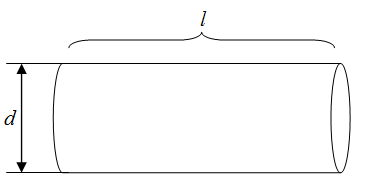



За время через трубу длиной протекает масса газа , которая равна:

(1)

где – плотность газа; – объем газа, который равен:



Где – площадь поперечного сечения трубы, которая равна:



Где – диаметр трубы.

Из двух последних выражений можем записать:



Подставим последнее выражение в (1):



Длина (расстояние пройденное газом) равна:



Где – скорость течения газа.

Из двух последних выражений можем записать:



Отсюда:



Подставим данные в последнее выражение:



Ответ: .