Лабораторная работа по Дискретной математике №1. ЛР№1.38 Иванов Л.Д. Решение На рисунке 2 изображена матрица смежности. Граф содержит 7 вершин. Т. к матрица смежности симметрична относительно главной диагонали, граф является неориентированным
 Скачать 291.74 Kb. Скачать 291.74 Kb.
|
|
Задачи ЛР1. Задание 1. По матрицам (рис. 2 и 3) построить диаграммы графов, определив предварительно вид данных матриц. 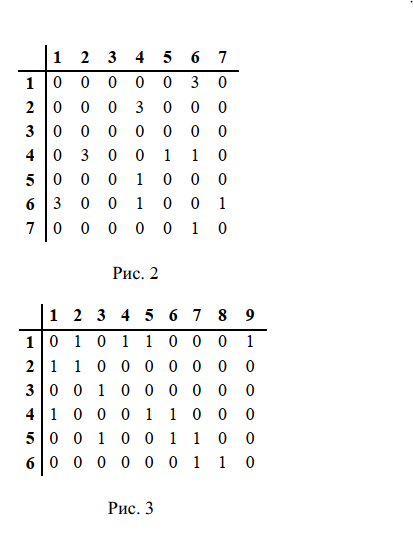 Решение: На рисунке 2 изображена матрица смежности. Граф содержит 7 вершин. Т.к. матрица смежности симметрична относительно главной диагонали, граф является неориентированным. Диаграмма графа имеет вид: 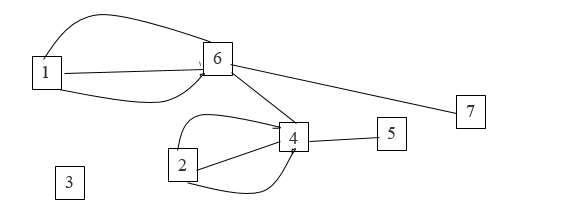 2.) На рисунке 3 изображена матрица инцидентности. Т.к. все значения в матрице положительные, то граф неориентированный. Граф содержит 6 вершин и 9 ребер. Диаграмма графа имеет вид: 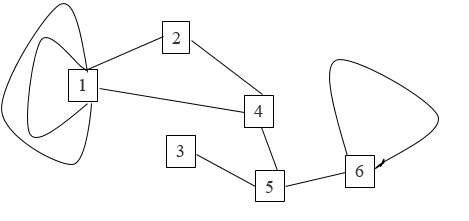                       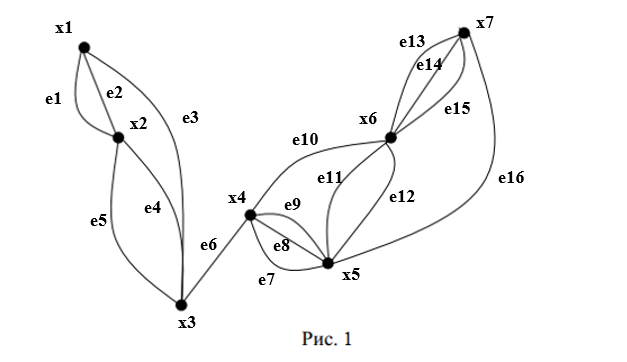 Решение: Наибольший минимальный маршрут между вершинами графа – маршрут при котором совершается обход всех вершин графа таким образом, что при отбрасывании какого-то ребра мы не обходим все вершины , и имеющий наибольшую возможную длину. Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность дальнейшего продвижения, означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина). Пусть x1 – начальная вершина. Перейдем из нее в вершину x2 по ребру е2, из вершины x2 в вершину x3 по ребру е5, из вершины x3 в вершину x4 по ребру е6, из вершины x4 в вершину x6 по ребру е10, из вершины x6 в вершину x7 по ребру е13. У вершины x7 нет смежных непосещенных вершин, вернемся к вершине x6. У вершины x6 нет смежных непосещенных вершин, вернемся к вершине x4. Перейдем из нее в вершину x5 по ребру е8. У вершины x5 нет смежных непосещенных вершин, вернемся к вершине x4. У вершины x4 нет смежных непосещенных вершин, вернемся к вершине x3. У вершины x3 нет смежных непосещенных вершин, вернемся к вершине x2. У вершины x2 нет смежных непосещенных вершин, вернемся к вершине x1. У вершины x1 нет смежных непосещенных вершин. Все вершины графа посещены. Алгоритм закончен. Максимальный маршрут: x1e2x2e5x3e6x4e10x6e13x7e13x6e10x4e8x5 .  Поиск в ширину означает, что мы обходим связный граф таким образом, что сначала мы рассматриваем родителя, потом по очереди рассматриваем множество его предков, потом рассматриваем предков его предков и т.д. . Пусть x1 – начальная вершина. Из вершины x1 можно попасть в x2 и x3: ребра e1, e3. У вершины x2 нет непосещенных смежных вершин. Из вершины x3 можно попасть в x4: ребро e6. Из вершины x4 можно попасть в x5 и x6: ребра e8 , e10. Из вершины x5 можно попасть в x7: ребро e16. У вершины x6 нет непосещенных смежных вершин. У вершины x7 нет непосещенных смежных вершин. Очередь пуста, все вершины графа были посещены. Алгоритм закончен Максимальный маршрут: x1e1x2e1x1e3x3e6x4e10x6e10x4e8x5e16x7 . Задание 3.Для каждой пары вершин графа (рис. 1) аналитическим способом вычислить количество маршрутов длины, равной 4, и выделить те пары вершин, для которых их количество ≥ 3, но не более 10. Выписать эти маршруты для какой-либо из выделенных пар. В описании маршрутов указывать вершины и ребра, входящие в него. Решение:  Запишем матрицу смежности графа. Элемент матрицы R: Запишем матрицу смежности графа. Элемент матрицы R: 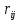 равен числу ребер, соединяющих i-ю и j-ю вершины графа равен числу ребер, соединяющих i-ю и j-ю вершины графа 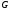 . .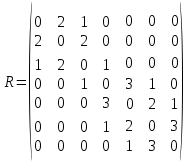 Возведем матрицу смежности в 4ю степень, получим матрицу, в которой каждый элемент равен количеству маршрутов длины 4 между вершинами i и j 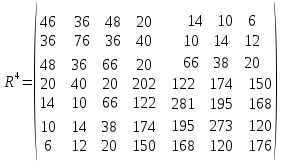 Получаем 6 маршрутов длины 4 между 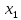 и и 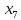 : x1e3x3e6x4e10x6e13x7 , x1e3x3e6x4e10x6e14x7, x1e3x3e6x4e10x6e15x7, : x1e3x3e6x4e10x6e13x7 , x1e3x3e6x4e10x6e14x7, x1e3x3e6x4e10x6e15x7,x1e3x3e6x4e7x5e16x7, x1e3x3e6x4e8x5e16x7, x1e3x3e6x4e9x5e16x7 . Получаем 10 маршрутов длины 4 между 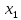 и и 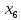 : x1e3x3e6x4e7x5e11x6 , x1e3x3e6x4e7x5e12x6, x1e3x3e6x4e8x5e11x6, : x1e3x3e6x4e7x5e11x6 , x1e3x3e6x4e7x5e12x6, x1e3x3e6x4e8x5e11x6,x1e3x3e6x4e8x5e12x6, x1e3x3e6x4e9x5e11x6, x1e3x3e6x4e9x5e12x6 , x1e1x2e4x3e6x4e10x6 , x1e1x2e5x3e6x4e10x6 , x1e2x2e4x3e6x4e10x6 , x1e2x2e5x3e6x4e10x6 . Задание 4. Построить матрицу метрики графа (рис. 1).  Решение: Найдем матрицу смежности графа G : 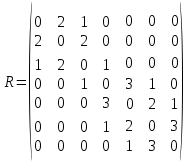 . .Найдем матрицу S= R+E 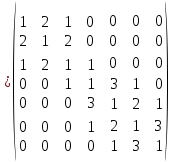 . .Вычислим M матрицу метрики заданного графа G за несколько шагов . Шаг 0 Диагональные элементы M заполняем нулями : M= 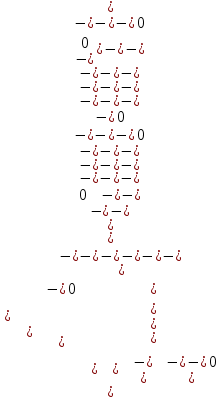 Шаг1 Заполняем свободные места в M единицами, если на соответствующих местах в матрице 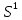 = S есть ненулевые элементы. = S есть ненулевые элементы.M= 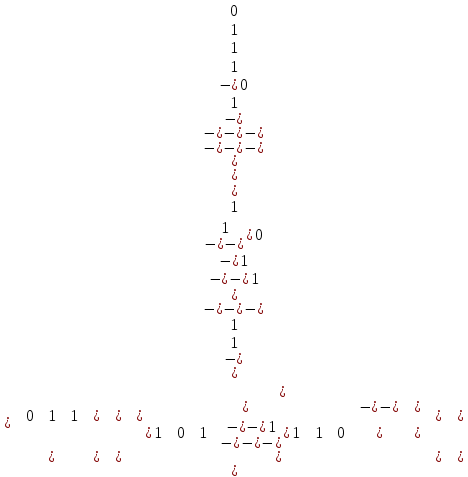 . .Шаг 2 Находим матрицу 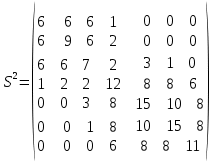 . . Заполняем свободные места в M двойками, если на соответствующих местах в матрице 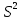 есть ненулевые элементы: есть ненулевые элементы:M= 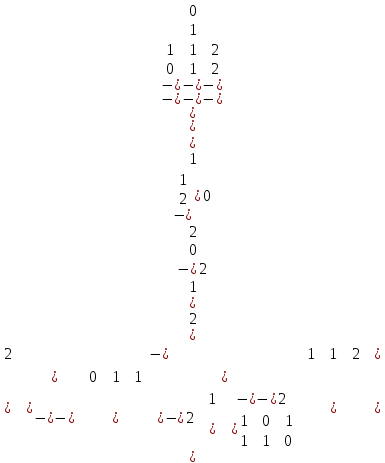 Шаг 3 Вычислим матрицу  . .Заполняем свободные места в M тройками, если на соответствующих местах в матрице 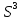 есть ненулевые элементы: есть ненулевые элементы:M= 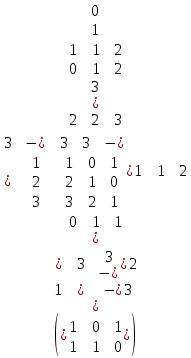 . .Шаг 4. Вычислим матрицу 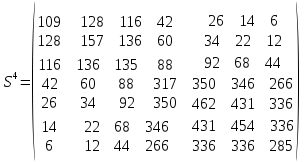 . . Заполняем свободные места в M четверками, если на соответствующих местах в матрице 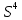 есть ненулевые элементы: есть ненулевые элементы:M= 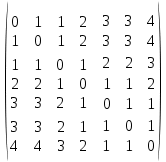 . .Ответ: Матрица M метрики графа G имеет вид 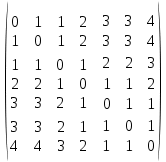 . .Задание 5.С помощью алгоритма Магу – Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов. Решение:  Найдем все максимальные пустые подграфы графа с помощью алгоритма Магу-Вейсмана.   5 2 Нарисуем скелет графа 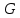       1       7 4  3  6 Составляем произведение 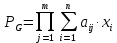 , где , где 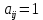 , если ребро скелета , если ребро скелета 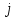 соединяет вершину скелета соединяет вершину скелета 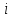 , ,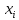 – логические переменные для которых выполняются правила : – логические переменные для которых выполняются правила : 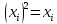 , , 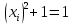 , , 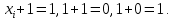 Преобразуем 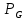 к минимальной бесскобочной форме: к минимальной бесскобочной форме: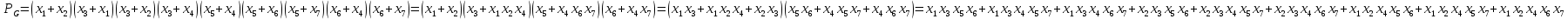 . .Для каждого слагаемого выполним дополнение до полной системы образующих 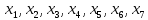 : :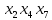 , , 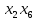 , ,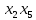 , , 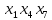 , , 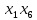 , ,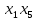 , ,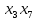 , ,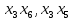 . .Получили максимальные пустые подграфы графа 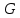 . .Тройка 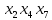 , , 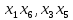 покрывает все вершины графа. Таким образом, для раскраски требуется минимум 3 цвета. Минимальная раскраска графа состоит из подграфов 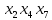 , , 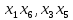 . .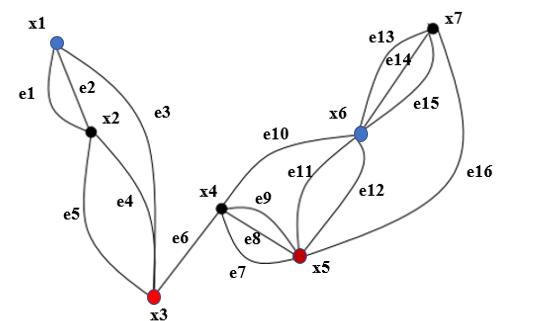 Ответ: Минимальная раскраска графа состоит из подграфов 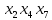 , , 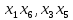 . .Задание 6. Определить число вершинного покрытия графа (рис. 1).  Решение: Вершинное покрытие – это такое множество S вершин графа, что у каждого ребра графа хотя бы один конец входит в S. Найдем минимальное вершинное покрытие. Выбираем случайное ребро e3 . Добавляем в S обе его вершины: S={x1,x3}. Удаляем все ребра ицидентные x1,x3 . 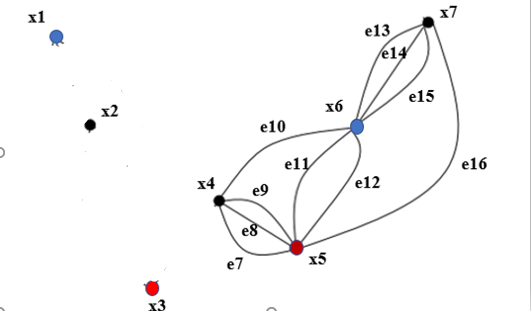 Выберем ребро e16. S={x1,x3 ,x5,x7} Удаляем все ребра ицидентные x5,x7 : 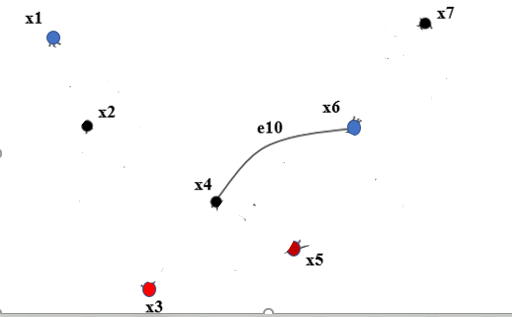 Выберем ребро e10 и получим вершинное покрытие S={x1,x3, x4,x6 x5,x7}. Число вершинного покрытия равно 6. Ответ: S={x1,x3, x4,x6 x5,x7}. Задание 7. Определить, содержит ли граф (рис. 1) эйлерову цепь или эйлеров цикл. Ответ обосновать. Решение:  Степенью вершины называется число ребер ицидентных данной вершине. Найдем все степени в графе : Deg(x1)=3, Deg(x2)=4, Deg(x3)=4, Deg(x4)=5, Deg(x5)=6, Deg(x6)=6, Deg(x7)=4 . Есть 2 вершины с нечетными степенями x1 и x4. Значит эйлерова цикла нет, но есть эйлерова цепь, между x1 и x4. Добавим фиктивное ребро между x1 и x4. Разобьем новый граф на простые циклы, найдем в нем эйлеров цикл и отбросим потом фиктивное ребро.  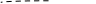 Получим 7 циклов: x1e3x3e6x4e9x1, x1e1x2e2x1, x2e4x3e5x2 , x4e10x6e13x7e16x5e7x4, x4e8x5e9x4, x5e11x6e12x5, x6e14x7e15x6. Отбросим фиктивное ребро и получим эйлерову цепь x1e3x3 x3e5x2 x2e1x1 x1e2x2 x2e4x3 x3e6x4 x4e10x6e13x7e16x5e7x4 x4e8x5 x5e11x6 x6e14x7 x7e15x6 x6e12x5 x5e9x4. Ответ : получим эйлерову цепь x1e3x3 x3e5x2 x2e1x1 x1e2x2 x2e4x3 x3e6x4 x4e10x6e13x7e16x5e7x4 x4e8x5 x5e11x6 x6e14x7 x7e15x6 x6e12x5 x5e9x4. Задание 8. Аналитическим способом определить число компонент связности графа. Решение: Аналитическим способом определить число компонент связности графа 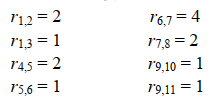 Решение Построим скелет графа 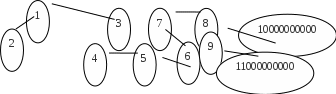 Найдем количество компонент связности K методом поиска в глубину. К=1 Из вершины 1 можем попасть в 2. У вершины 2 нет смежных непосещенных вершин, вернемся к 1. Из вершины 1 можем попасть в 3. У вершины 3 нет смежных непосещенных вершин. Компонента связности найдена. К=2 Из вершины 4 можем попасть в 5. Из 5 в 6. Из 6 в 7. Из 7 в 8 .У вершины 8 нет смежных непосещенных вершин, вернемся к 7. У вершины 7 нет смежных непосещенных вершин, вернемся к 6. У вершины 6 нет смежных непосещенных вершин, вернемся к 5. У вершины 5 нет смежных непосещенных вершин, вернемся к 4. У вершины 4 нет смежных непосещенных вершин. Компонента связности найдена. К=3 Из вершины 9 можем попасть в 10. У вершины 10 нет смежных непосещенных вершин, вернемся к 9. Из вершины 9 можем попасть в 11. У вершины 11 нет смежных непосещенных вершин, вернемся к 9. У вершины 9 нет смежных непосещенных вершин. Компонента связности найдена. . Все вершины графа были посещены. Ответ: К=3. |
