Лабораторная 1в18. Лабораторная работа 1 по дисциплине Дискретная математика
 Скачать 412.71 Kb. Скачать 412.71 Kb.
|
1 2 Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра компьютерных систем в управлении и проектировании (КСУП) ОТЧЕТ Лабораторная работа № 1 по дисциплине «Дискретная математика» Задание 1.По матрицам (рис. 2 и 3) построить диаграммы графов, определив предварительно вид данных матриц. 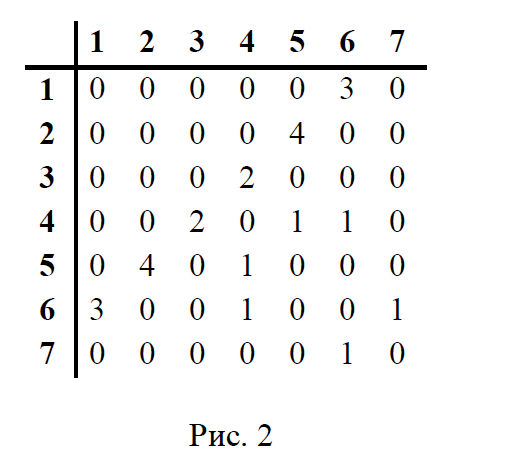 1 5 6 7  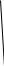  4 1 1 3 1 2 3 4  2 Ответ: на рисунке 2 изображена матрица смежности  р2 1 5 6 р7     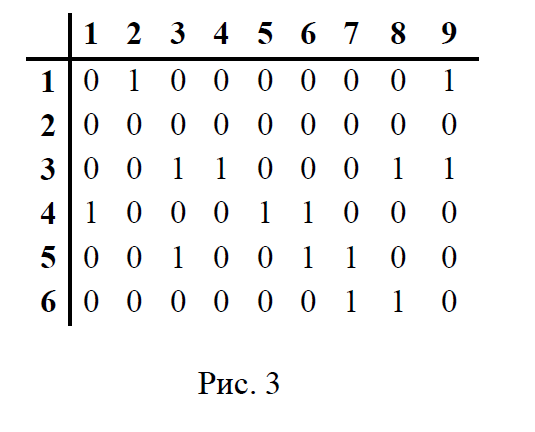 4 3 2    р5 р6 р3 р8 р9 р1 р4 Ответ: на рисунке 3 изображена матрица инцидентности Задание 2.Методами поиска «в глубину» и «в ширину» найти наибольший минимальный маршрут между вершинами графа (рис. 1).  x1 x2 x5 x3 x8 x7 x6 x4 u1 u2 u7 u4 u5 u3 u8 u9 u11 u10 u14 u15 u12 u13 u6 u16 Решение: Наибольший минимальный маршрут между вершинами графа – маршрут при котором совершается обход всех вершин графа таким образом, что при отбрасывании какого-то ребра мы не обходим все вершины , и имеющий наибольшую возможную длину. Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность дальнейшего продвижения, означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина). Пусть x1 – начальная вершина. Перейдем из нее в вершину x2 по ребру u1, из вершины x2 в вершину x3 по ребру u5, из вершины x3 в вершину x6 по ребру u8, из вершины x6 в вершину x5 по ребру u9, из вершины x5 в вершину x7 по ребру u12, из вершины x7 в вершину x8 по ребру u14 У вершины x8 нет смежных непосещенных вершин, вернемся к вершине x7. У вершины x7 нет смежных непосещенных вершин, вернемся к вершине x5. Перейдем из нее в вершину x4 по ребру u10. У вершины x4 нет смежных непосещенных вершин, вернемся к вершине x5. У вершины x5 нет смежных непосещенных вершин, вернемся к вершине x6. У вершины x6 нет смежных непосещенных вершин, вернемся к вершине x3. У вершины x3 нет смежных непосещенных вершин, вернемся к вершине x2. У вершины x2 нет смежных непосещенных вершин, вернемся к вершине x1. У вершины x1 нет смежных непосещенных вершин. Все вершины графа посещены. Алгоритм закончен. Ответ: Максимальный маршрут: x1 u 1x2u5x3u8x6u9x5u12x7u14x8u14x7u12x5 u10x4. Поиск в ширину означает, что мы обходим связный граф таким образом, что сначала мы рассматриваем родителя, потом по очереди рассматриваем множество его предков, потом рассматриваем предков его предков и т.д. . Пусть x1 – начальная вершина. Из вершины x1 можно попасть в x2 и x5: ребра р1, р3. Из вершины x2 можно попасть в x3: ребро e5. Из вершины x5 можно попасть в x4, x6, x7, x8: ребро р10, р9, р12, р13. У вершины x3 нет непосещенных смежных вершин У вершины x4 нет непосещенных смежных вершин. У вершины x6 нет непосещенных смежных вершин. У вершины x7 нет непосещенных смежных вершин. У вершины x8 нет непосещенных смежных вершин. Очередь пуста, все вершины графа были посещены. Алгоритм закончен Ответ: Максимальный маршрут: x1 - u1x2, u3x5; x2 - u5x3; x5 - u10x4, u9x6, u12x7, u13x8 Задание 3.Для каждой пары вершин графа (рис. 1) аналитическим способом вычислить количество маршрутов длины, равной 4, и выделить те пары вершин, для которых их количество ≥ 3, но не более 10. Выписать эти маршруты для какой-либо из выделенных пар. В описании маршрутов указывать вершины и ребра, входящие в него. Запишем матрицу смежности графа. Элемент матрицы R: равен числу ребер, соединяющих i-ю и j-ю вершины графа .  Возведем матрицу смежности в 4ю степень, получим матрицу, в которой каждый элемент равен количеству маршрутов длины 4 между вершинами i и j  В данном графе минимальное количество маршрутов, длины 4, между вершинами составляет 22.Таким образом, выделить те пары вершин, для которых их количество ≥ 3, но не более 10 не представляется возможным. Задание 4. Построить матрицу метрики графа (рис. 1). Шаг 1. Задаём матрицу метрики M = (mi,j)n×n. Размерность матрицы M равна размерности матрицы R. Все элементы mi,j матрицы M не определены.
М
R
S=R+E Шаг 2. Начальное значение степени k матрицы S равно «1»: k = 1. ∀mi i присваиваем значение «0», на основании 1-ой аксиомы Фрише.
M Шаг 3. Всем элементам mi,j, значения которых не определены, присвоить значение степени k, если соответствующие им элементы матрицы Sk ≠ 0. (Значения элементов mi,j определяются только один раз.)
M Шаг 4. Повышаем степень k матрицы S: k = k + 1.
M Шаг 5. Проверяем, является ли матрица Sk−1 устойчивой. Матрица Sk называется устойчивой, если Sk = Sk+1. Данная матрица не является устойчивой матрицей Шаг 6. Всем элементам mi,j, значения которых не определены, присвоить значение степени k=2, если соответствующие им элементы матрицы Sk ≠ 0.
M Ответ: матрица метрики вид
1 2 |
