Дифференциальное исчисление функции двух переменных. Дифференциальное исчисление функций двух переменных. Решение находим частные производные 1го порядка функции

• Название: Решение находим частные производные 1го порядка функции
• Анкор: Дифференциальное исчисление функции двух переменных
• Дата: 14.02.2022
• Размер: 415 Kb.
• Имя файла: Дифференциальное исчисление функций двух переменных.doc
• Тип: Решение; #361909

Задание 1. Для функции :

1. 
   найти частные производные 1-го порядка и дифференциал 1-го порядка в точке ;
   
2. 
   найти частные производные 2-го порядка и дифференциал 2-го порядка в точке :
   

,

Решение:

1. 
   находим частные производные 1-го порядка функции: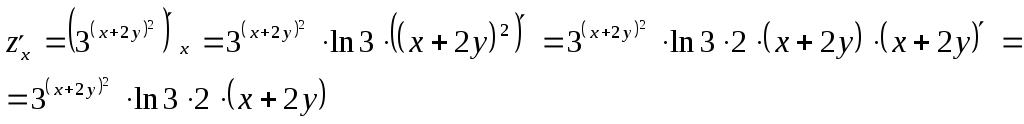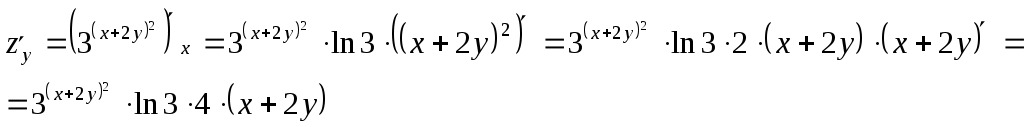
   

Полный дифференциал первого порядка функции в точке имеет вид:

.

Находим значения частных производных в точке :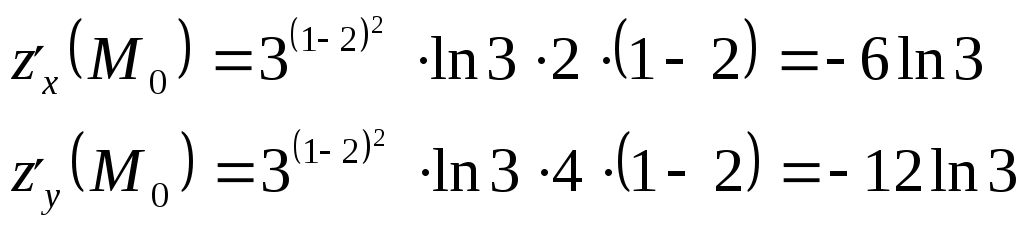



Находим полный дифференциал первого порядка функции:

2. 
   Находим частные производные 2-го порядка функции: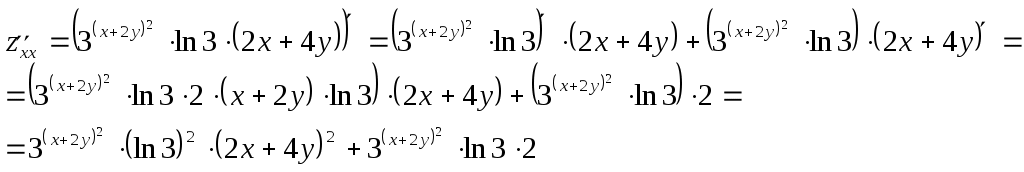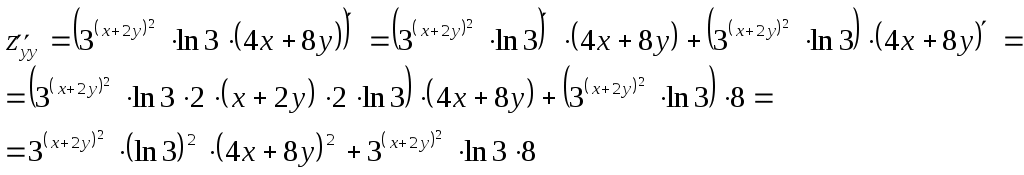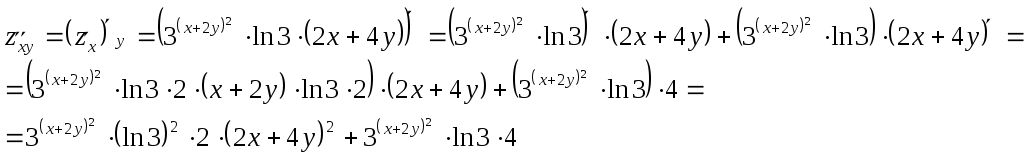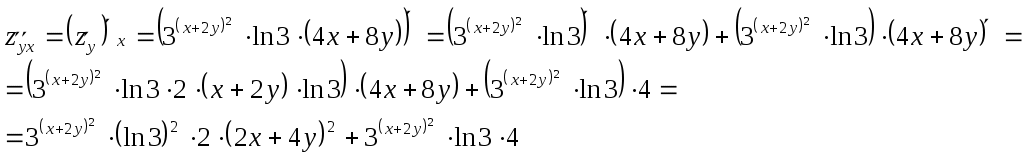
   

Находим значения частных производных второго порядка в точке :







Находим полный дифференциал второго порядка функции:


Задание 2. Найти частные производные в т. функции, заданной неявно:

,

Решение:

Вычисляем частные производные: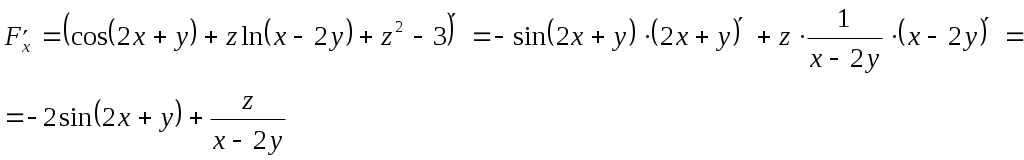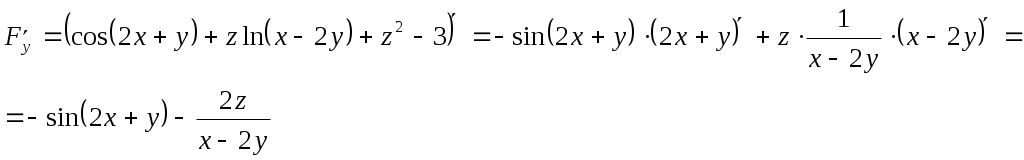





В результате применяя формулы 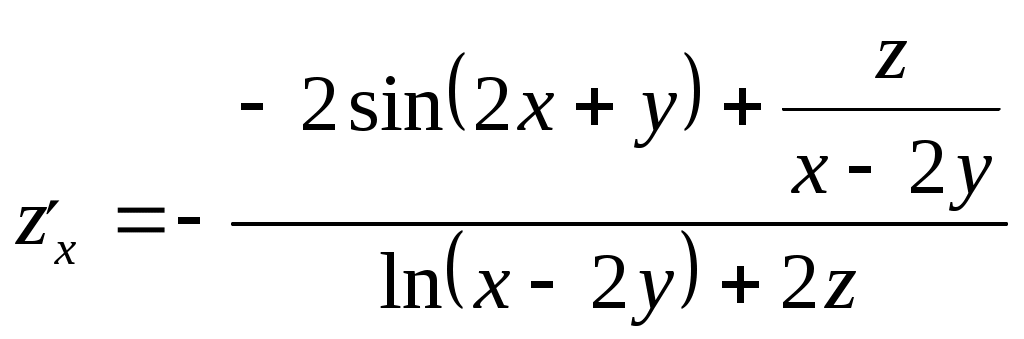, ,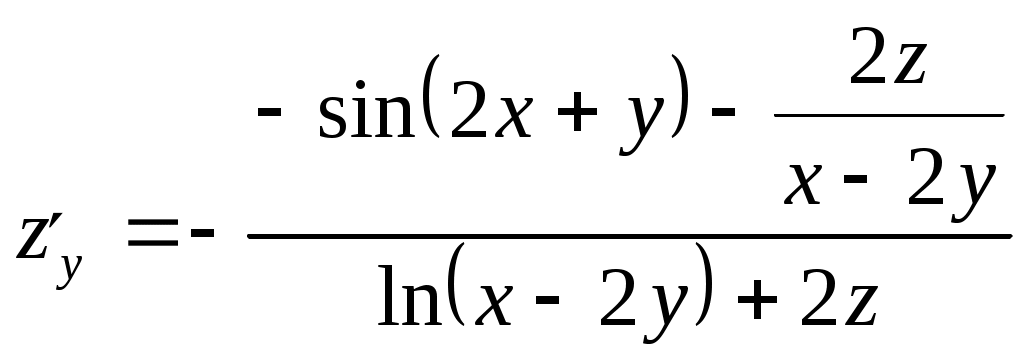 получим

,



Вычислим частные производные в точке :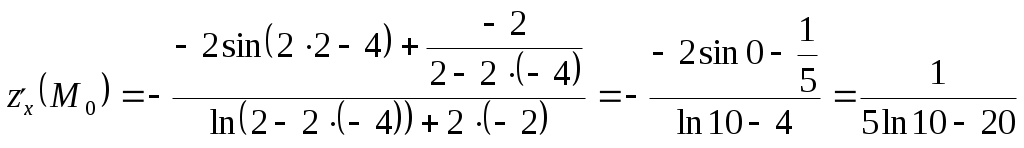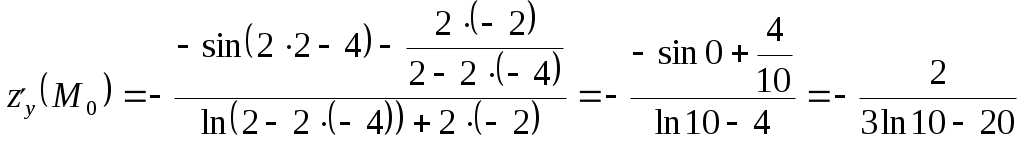

,

.
Задание 3. Для функции , где , , найти полную производную :



Решение:

Вычисляем частные производные :





Находим производные от функций одной переменной:

,



Тогда полная производная, найденная по формуле , имеет вид:



Задание 4. Для функции , где , найти полную производную :



Решение:

Вычисляем частные производные :

,

.

Находим производную от функций одной переменной:

,

Тогда полная производная, найденная по формуле , имеет вид:


Задание 5. Для функции , где , найти частные производные :



Решение:

Вычисляем частные производные :

,

.

Далее вычисляем частные производные :








В результате частные производные находим по формулам:

и




Задание 6.Составить уравнения касательной плоскости и нормали к поверхности, заданной:

1. 
   функцией в точке ;
   
2. 
   в точке .
   

Решение:

1. 
   Вычисляем частные производные первого порядка функции:
   

Находим значения частных производных в точке :





Уравнение касательной плоскости находим по формуле:





Уравнение нормали находим по формуле:

2. 
   
   

В данном случае функция задана в неявном виде, частные производные вычислим по формулам:





Вычисляем частные производные функции:











Находим значения частных производных в точке :





Уравнение касательной плоскости находим по формуле:





Уравнение нормали находим по формуле: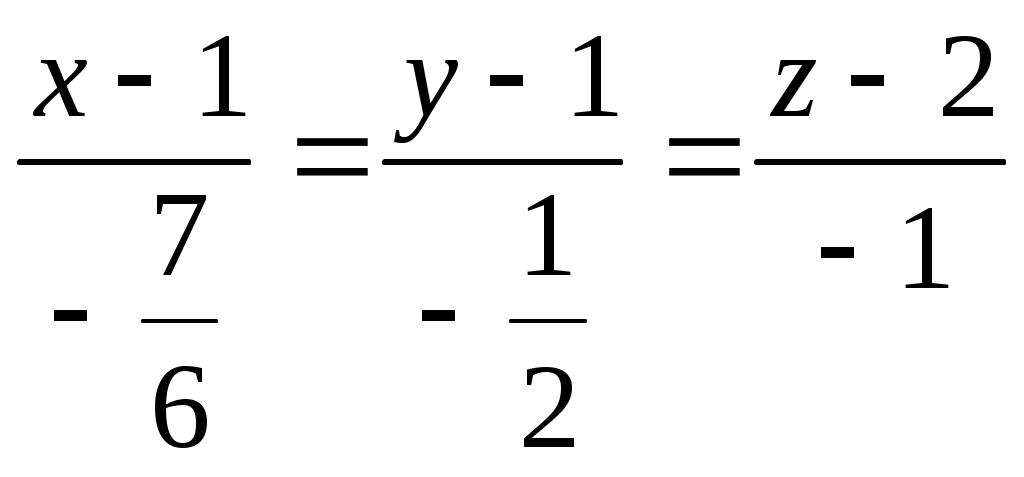




Задание 7. Найти критические точки функции и исследовать их характер:



Решение:

Найдем частные производные функции:





Приравнивая их к нулю, находим стационарные точки функции: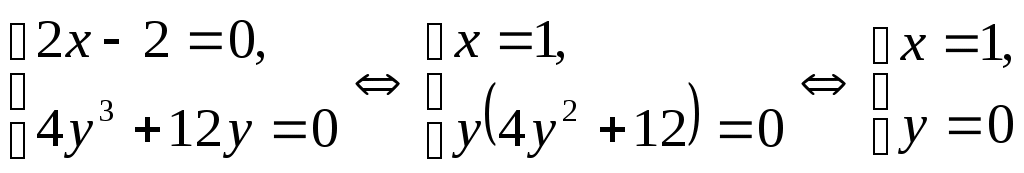



Таким образом, стационарная точка функции: .

Вычислим частные производные второго порядка функции:







Тогда определитель имеет вид:



Вычислим значения определителя в стационарных точках и воспользуемся достаточным условием точки локального экстремума.

В точке :

, следовательно в точке есть локальный экстремум. Так как, , то точка - точка локального минимума.

Вычислим значение функции в точке :

.

Таким образом, точка локального минимума , .

Задание 8. Найти наибольшее и наименьшее значения функции в заданной замкнутой ограниченной области:



Решение:

Определим стационарные точки функции. Для этого найдем частные производные функции:





Приравнивая их к нулю, находим стационарные точки функции: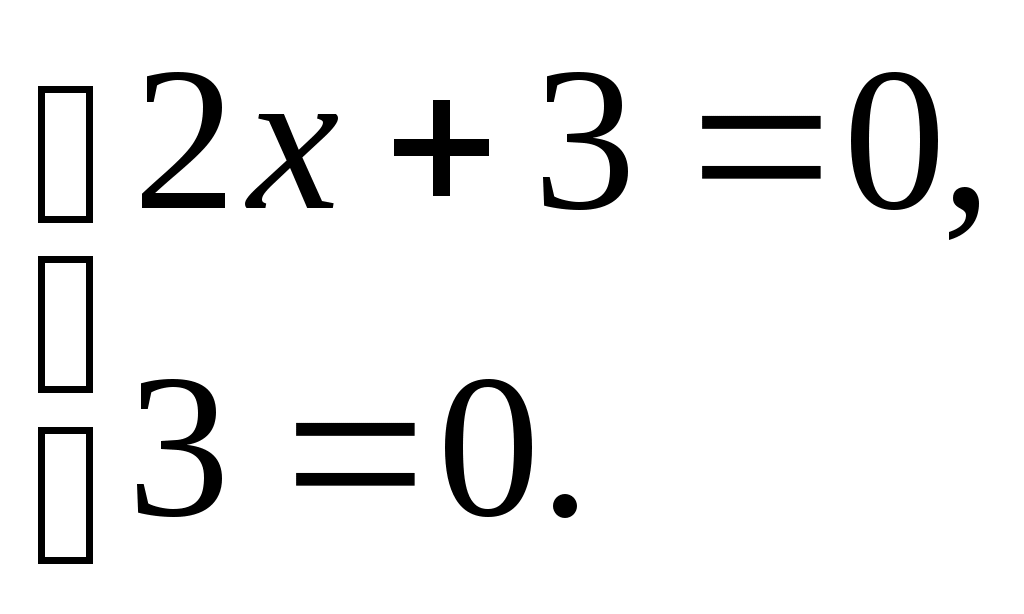



Полученная система не имеет решения, значит, стационарных точек функция не имеет.

Исследуем экстремумы функции на границе множества . Подставим уравнение прямой в функцию . Получится функция



Найдем ее наибольшее и наименьшее значения на отрезке . Находи первую производную и приравниваем ее к нулю: , тогда . Обозначим точку . Полученная точка не входит в замкнутую область.

При , значение функции . При , значение функции

Подставим уравнение прямой в функцию . Получится функция



Найдем ее наибольшее и наименьшее значения на отрезке . Находим первую производную функции и приравниваем ее к нулю: , тогда . Обозначим точку . Вычислим значение функции в этой точке . При , значение функции . При получается точка , значение функции .

Подставим уравнение прямой в функцию . Получится функция



Найдем ее наибольшее и наименьшее значения на отрезке . Находим первую производную функции и приравниваем ее к нулю: , тогда . Обозначим точку . Вычислим значение функции в этой точке .

При получаем точку , значение функции . При получаем точку , значение функции .

Выпишем полученные значения функций:

, , , .

Следовательно, наибольшего значения функция достигает в точке , а наименьшего в точке .

Задание 9. Найти градиент функции и производную по направлению вектора в точке :



Решение:

По условию задачи сказано, что в качестве направления выступает вектор . Формула вычисления производной функции по направлению имеет вид:

, где - значения частных производных функции в точке , - направляющие косинусы вектора .

Находим частные производные:



,

и значения частных производных в точке :



.

Вычисляем направляющие косинусы вектора :



.

В результате производная функции 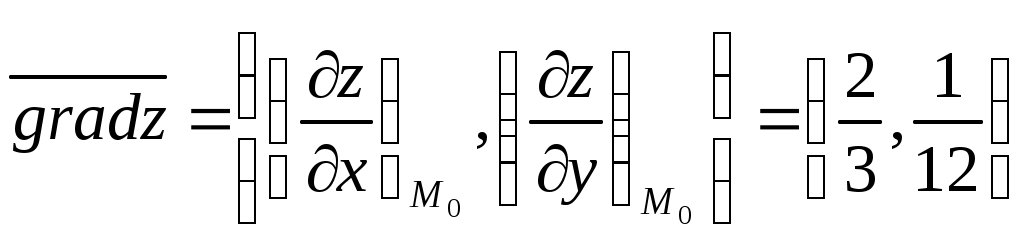по направлению вектора будет равна:



Градиент функции есть вектор, координатами которого являются частные производные первого порядка

.

В точке градиент функции определяется вектором

.

Тогда