Задание по методам оптимизации (1). Решение. Найдем частные производные функции Найдем вторые частные производные Получаем градиент
 Скачать 224.74 Kb. Скачать 224.74 Kb.
|
|
1. Решить методом Ньютона-Рафсона 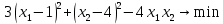 , , 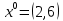 Решение. Найдем частные производные функции: 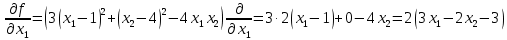 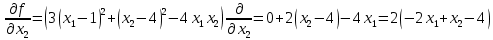 Найдем вторые частные производные: 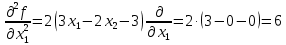 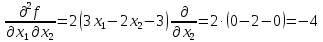 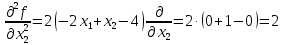 Получаем градиент: 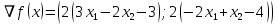 . .Гессиан примет вид: 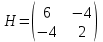 . .Найдем градиент в точке 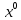 : : 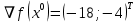 . .Находим обратный гессиан: 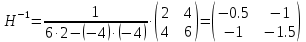 Выполняем приближение по формуле: 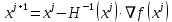 Получаем: 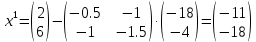 Найдем градиент в точке 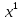 : : 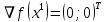 . Тогда: . Тогда: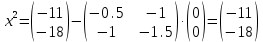 Так как 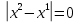 , достигнут минимум: , достигнут минимум: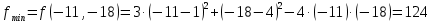 2. Решить графически и аналитически с помощью необходимых и достаточных условий 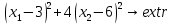 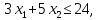 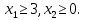 Решение. Решим задачу графическим способом. Так как 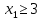 и и 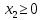 , то область допустимых решений будет лежать первой координатной четверти. , то область допустимых решений будет лежать первой координатной четверти.На первой координатной четверти строим прямые, порождаемые системой ограничений. Для построения прямых заменяем знаки неравенства в системе ограничений на знаки равенства.  Относительной каждой прямой определяем полуплоскость, соответствующую исходным неравенствам. Область допустимых решений (ОДР) лежит ниже прямой 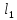 и правее прямой и правее прямой 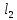 : :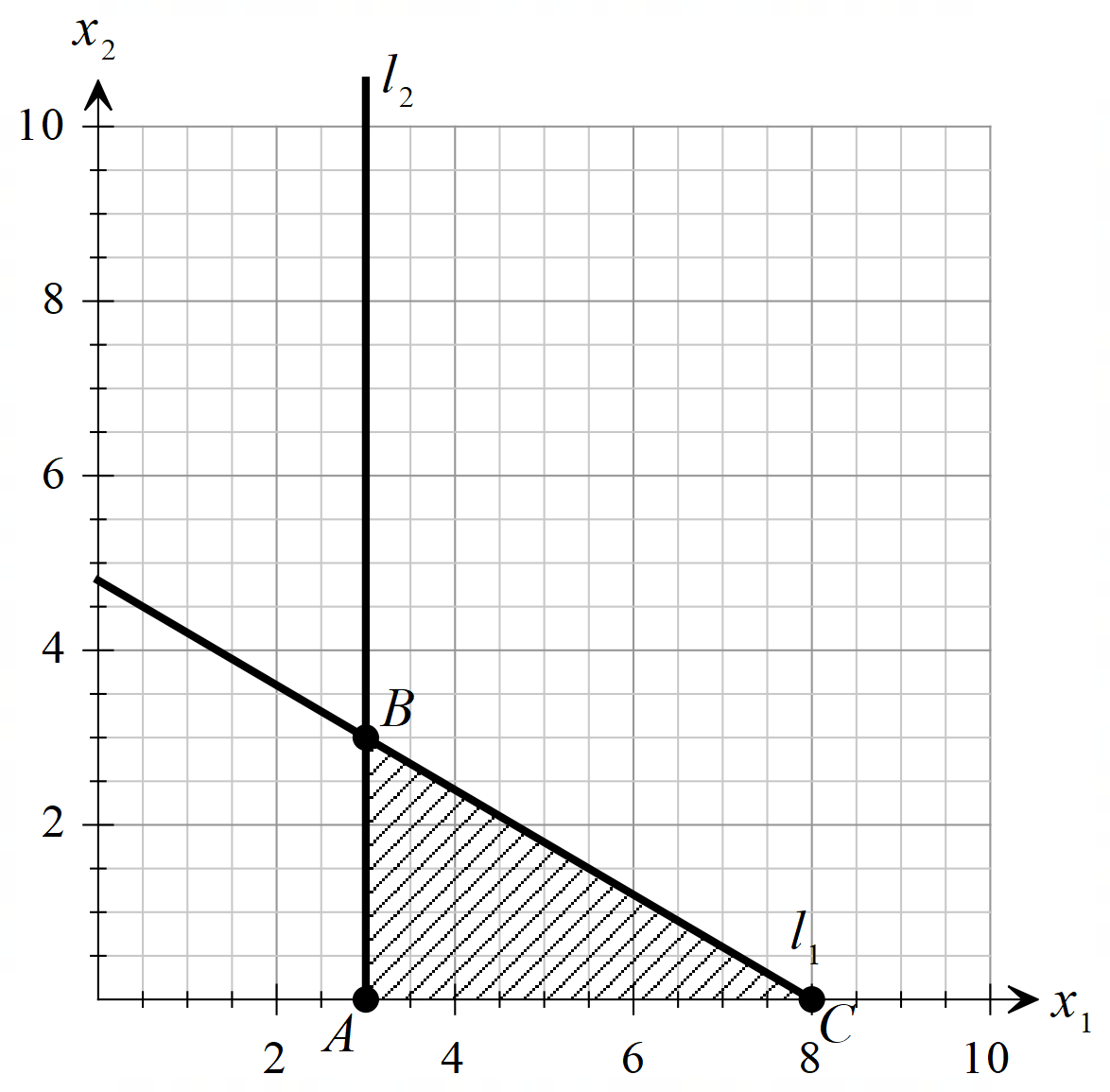 Преобразуем целевую функцию, приравняв ее к константе: 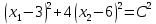 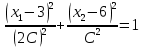 Получили эллипс с центром в точке (3; 6), при этом радиус по оси 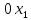 больше радиуса по оси больше радиуса по оси 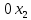 в два раза. в два раза.Изменяя константу 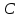 будем перемещать целевую функцию: будем перемещать целевую функцию: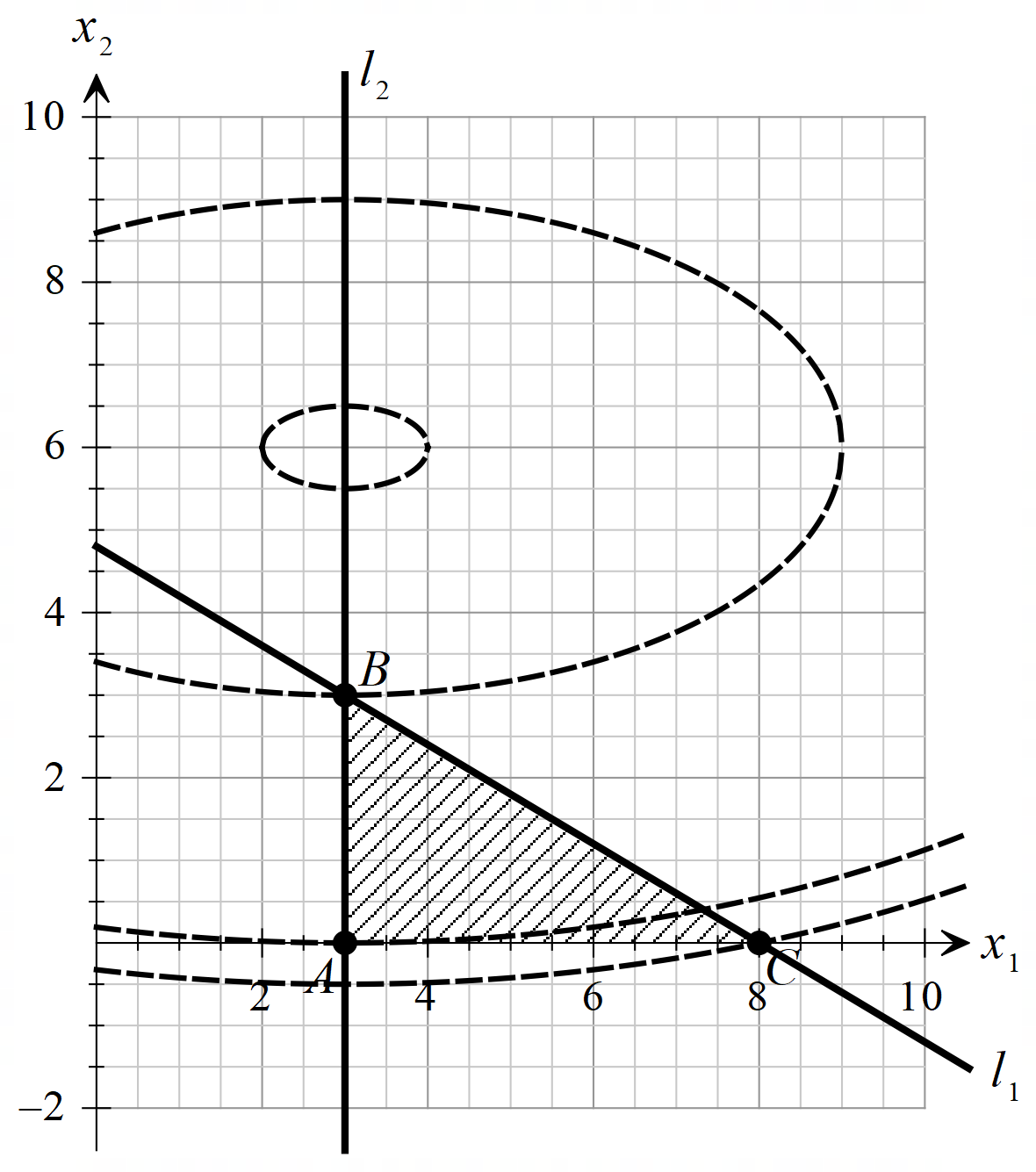 По графику видно, что минимум функции достигается в точке 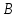 , т.к. в ней эллипс имеет меньшие радиусы и выходит из области определения. Точка , т.к. в ней эллипс имеет меньшие радиусы и выходит из области определения. Точка 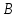 находится на пересечении прямых находится на пересечении прямых 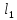 и и 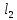 : :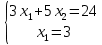 Решая систему, получаем 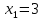 и и 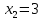 , тогда: , тогда: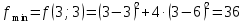 Максимум функции достигается в точке 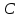 , которая находится на пересечении прямой , которая находится на пересечении прямой 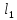 и оси и оси 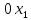 : :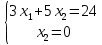 Решая систему, получаем 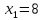 и и 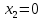 , тогда: , тогда: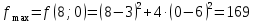 Решим задачу аналитически. Для того, чтобы точка была точкой локального условного экстремума функции относительно уравнений связи необходимо, чтобы эта точка удовлетворяла системе уравнений Лагранжа: 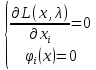 Здесь 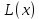 – функция Лагранжа вида – функция Лагранжа вида 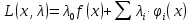 , где , где 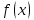 – целевая функция; – целевая функция; 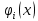 – ограничения вида – ограничения вида 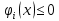 или или 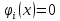 . .В данном случае функция Лагранжа примет вид: 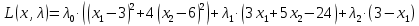 Находим частные производные: 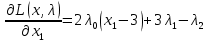 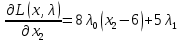 Получаем: 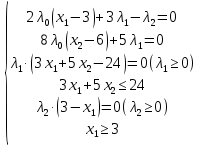 Рассмотрим случай 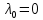 : :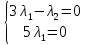 Откуда 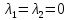 . Т.о., при . Т.о., при 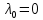 экстремумов нет, следовательно, экстремумов нет, следовательно, 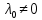 . .Из условий дополняющей нежесткости получаем: либо 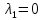 , либо , либо 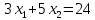 , а также либо , а также либо 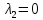 , либо , либо 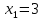 . .Положим 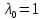 (локальный минимум). Тогда из первых двух уравнений получаем: (локальный минимум). Тогда из первых двух уравнений получаем: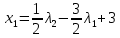 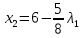 Из условий дополняющей нежесткости получаем систему: 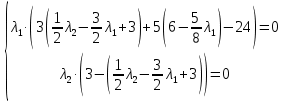 Откуда: 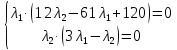 Рассмотрим случай 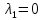 , тогда , тогда 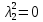 или или 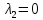 . Т.о., при . Т.о., при 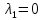 экстремумов нет, следовательно, экстремумов нет, следовательно, 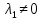 . .Рассмотрим случай 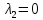 , тогда , тогда 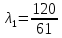 . Получаем . Получаем 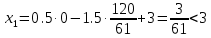 . Следовательно, . Следовательно, 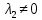 . Тогда: . Тогда: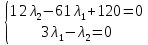 Откуда 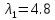 , , 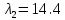 . Тогда . Тогда 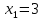 , , 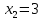 , , 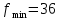 . .Таким образом, в точке (3; 3) достигает минимума, равного 36. Положим 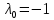 (локальный максимум). Тогда из первых двух уравнений получаем: (локальный максимум). Тогда из первых двух уравнений получаем: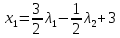 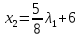 Из условий дополняющей нежесткости получаем систему: 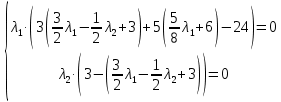 Откуда: 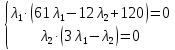 Рассмотрим случай 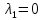 , тогда , тогда 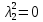 или или 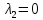 . Т.о., при . Т.о., при 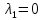 экстремумов нет, следовательно, экстремумов нет, следовательно, 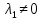 . .Рассмотрим случай 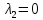 , тогда , тогда 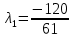 . Тогда: . Тогда: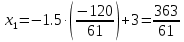 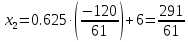 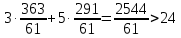 Условие первого ограничения не выполняется, поэтому 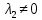 . . Рассмотрим случай 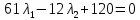 : :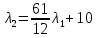 Подставляя, получаем: 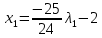 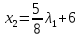 Из краевого ограничения 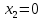 следует следует 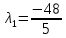 , тогда , тогда 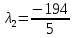 . Получаем . Получаем 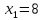 . Так как . Так как 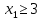 , все условия выполняются. , все условия выполняются.Рассмотрим случай 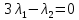 : :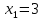 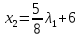 Из краевого ограничения 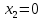 получаем получаем 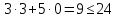 , все условия выполняются. , все условия выполняются.Получаем 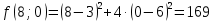 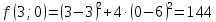 Таким образом, в точке (8; 0) достигает минимума, равного 169. 3. Решить методом возможных и подходящих направлений 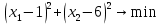 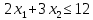 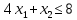 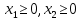 Решение. Найдем частные производный целевой функции: 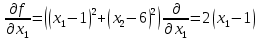 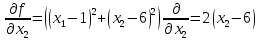 Получаем вектор градиент 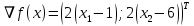 Зададим 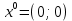 , тогда: , тогда: 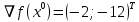 , длина которого , длина которого 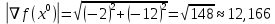 . .Координаты следующей точки: 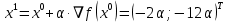 . .Найдём такие значения параметра, чтобы новая точка принадлежала области допустимых решений задачи: 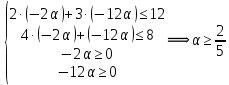 Градиент в точке 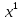 : : 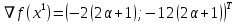 . . Из соображений 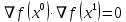 находим максимальное значение параметра находим максимальное значение параметра 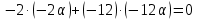 Откуда 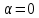 . .Поскольку это значение располагается левее отрезка 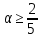 , нужно принять , нужно принять 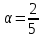 , однако это значение не даёт перехода в новую точку, поскольку текущая точка является наилучшей по данному направлению. , однако это значение не даёт перехода в новую точку, поскольку текущая точка является наилучшей по данному направлению.Ограничения 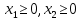 активны в точке активны в точке 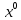 . Обозначим вектора коэффициентов при переменных . Обозначим вектора коэффициентов при переменных 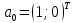 . . 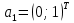 . Тогда выберем направление . Тогда выберем направление 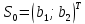 из условия равенства нулю скалярного произведения векторов из условия равенства нулю скалярного произведения векторов 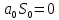 и и 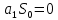 : :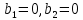 Длина вектора 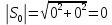 . .Так как скалярное произведение векторов 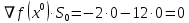 , то найденная точка является искомым оптимальным решением. , то найденная точка является искомым оптимальным решением.Значение функции в точке (0; 0): 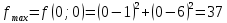 |
