задачи физика. задачи физика зима. Решение Напряженность поля, созданная первой нитью (1) где электрическая постоянная
 Скачать 36.83 Kb. Скачать 36.83 Kb.
|
|
Задача 1.13 Две бесконечные прямолинейные параллельные нити находятся на расстоянии d=0,5 м друг от друга. Линейные плотности электрического заряда на них составляют 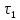 =3 мкл/м и =3 мкл/м и 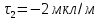 . Найти силу, действующую на единицу длины нити. . Найти силу, действующую на единицу длины нити.Д  ано: Задача 1.13 ано: Задача 1.13d = 0,5 м Решение 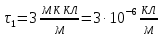    --- --- 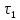 ---- ----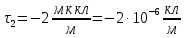 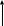 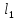 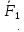 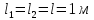    --- --- 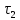 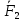 ---- ----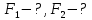 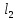 Напряженность поля, созданная первой нитью: 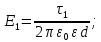 (1) (1)где 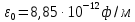 - электрическая постоянная - электрическая постоянная𝜀 - диэлектрическая проницаемость среды; d - расстояние между нитями; 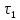 - линейная плотность заряда на первой нити. - линейная плотность заряда на первой нити.Заряд, приходящийся на единицу длины второй заряженной нити: 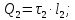 (2) (2)где 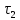 - линейная плотность заряда на второй нити. - линейная плотность заряда на второй нити.Сила, с которой электрическое поле первой нити действует на единицу длины второй нити: 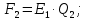 (3) (3)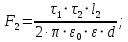 (4) (4)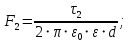 (5) (5)Заряд, приходящийся на единицу длины первой заряженной нити: 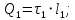 (6) (6)где 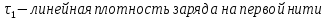 Сила, с которой электрическое поле второй нити действует на единицу длины первой нити: 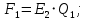 (7) (7)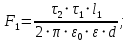 (8) (8)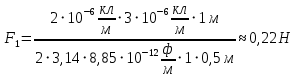 ; ;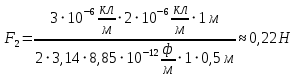 . .Ответ: 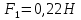 , , 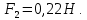 З  адача 1.43. Найти отношение скоростей ионов адача 1.43. Найти отношение скоростей ионов 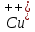 и и 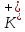 , прошедших одинаковую разность потенциалов. , прошедших одинаковую разность потенциалов.Дано: Решение: 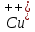 Со стороны электрического поля на заряженную Со стороны электрического поля на заряженную 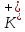 частицу действует сила частицу действует сила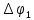 = =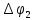 = =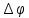 F=q∙E F=q∙Eгде q- заряд частицы ; E- напряженность 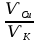 - ? электрического поля. Частицы под действием - ? электрического поля. Частицы под действием поля начинают двигаться. Работа поля A=q∙ 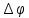 (1) (1)идет на увеличение их кинетических энергий 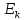 = =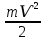 =q∙ =q∙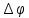 (2) (2)отсюда Ѵ= 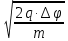 (3) (3)Для первой частицы 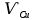 = =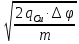 (4) (4)Для второй частицы 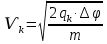 (5) (5)Из уравнений (4) и (5) определим отношение скоростей ионов 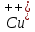 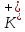 , прошедших одинаковую разность потенциалов. , прошедших одинаковую разность потенциалов.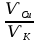 = =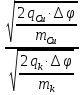 = =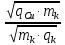 где 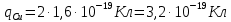 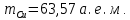 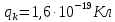 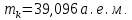 Подставим числовые значения 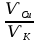 = = 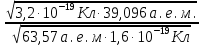 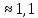 Ответ: 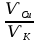 = 1,1 = 1,1Задача 1.73. При внешнем сопротивлении 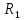 =8 Ом сила тока в цепи =8 Ом сила тока в цепи 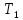 =0,8 А, при сопротивлении =0,8 А, при сопротивлении 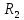 =15 Ом сила тока =15 Ом сила тока 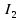 = 0,5 А. Определить силу тока = 0,5 А. Определить силу тока 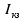 короткого замыкания источника ЭДС. короткого замыкания источника ЭДС.Д  ано: Решение ано: Решение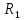 =8 Ом Ток короткого замыкания источника ЭДС определяется =8 Ом Ток короткого замыкания источника ЭДС определяется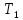 =0,8 А по закону Ома для участка цепи =0,8 А по закону Ома для участка цепи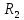 =15 Ом =15 Ом 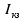 = =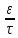 (1) (1) 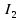 = 0,5 А где 𝜀- ЭДС источника тока = 0,5 А где 𝜀- ЭДС источника тока 𝛕-внутреннее сопротивление источника тока. Запишем 𝛕-внутреннее сопротивление источника тока. Запишем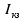 -? закон Ома для полной цепи при внешних сопротивлениях -? закон Ома для полной цепи при внешних сопротивлениях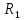 и и 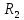 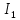 = =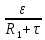 (2) (2) 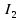 = =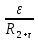 (3) (3)Из уравнений (2) и (3) 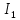 ( (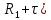 = =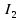 ( (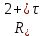 Отсюда находим внутреннее сопротивление источника ЭДС 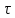 = =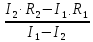 (4) (4)Из уравнений (1) и (2) 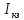 ∙ ∙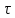 = =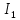 ( (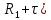 (5) (5)Из уравнений (4) и (5) определим ток короткого замыкания источника ЭДС 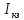 = =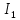 ( (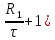 = =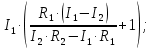 Представим числовые значения: 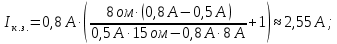 Ответ: 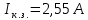 . .Задач 2.13. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи I= 200 A. Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине. Д 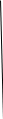 ано: Решение ано: Решение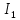 = =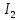 =I=200 A Согласно принципу суперпозиции полей =I=200 A Согласно принципу суперпозиции полей a=b результирующая сила 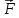 , действующая на рамку , действующая на рамку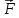 = =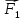 + +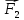 + +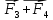 F-? 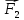 = - = - 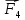 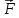 = = 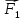 + +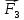 F= 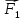 - -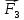 I            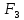 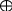 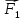 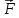 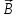   b 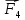 Сила Ампера, действующая на два проводника с токами 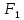 = = 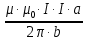 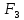 = =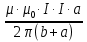 F= 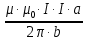 ( (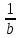 - - 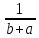 ) )т.к b=a, то сила F, действующая на рамку с током F= 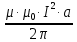 ( (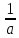 - - 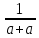 ) = ) = 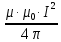 где 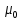 =4 =4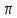 ∙ ∙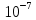 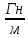 - магнитная проницаемость - магнитная проницаемость 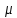 - магнитная проницаемость среды ( - магнитная проницаемость среды (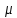 =1) =1)Подставим числовые значения F= 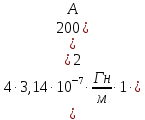 Ответ: F 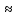 0,004 H 0,004 HЗадача 2.43 Альфа-частица влетела в скрещенные под прямым углом магнитное (B=5 мТл) и электрическое (Е=30 кв/м) поля. Определить ускорение а альфа-частицы в начальный момент времени, если ее скорость Ѵ ( 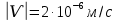 ) перпендикулярна векторам В и Е, причем силы, действующие со стороны этих полей, противоположно направлены. ) перпендикулярна векторам В и Е, причем силы, действующие со стороны этих полей, противоположно направлены.Д  ано: Решение ано: Решение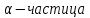 Скорость Скорость 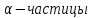 влетевшей в магнитное влетевшей в магнитное В=5мТл=0,005 тл поле: Е =30 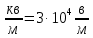 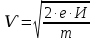 (1) (1)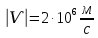 Разложим скорость Ѵ на две составляющие Разложим скорость Ѵ на две составляющие 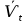 - - 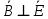 составляющую скорость, направляющую вдоль составляющую скорость, направляющую вдоль а - ? силовых линий магнитного поля и 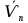 - составляю- - составляю-щую направляющую перпендикулярно к вектору 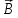 (индукции магнитного поля). По условии задачи необходимо определить ускорение 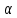 -частицы, где ее скорость -частицы, где ее скорость 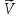 перпендикулярно векторам перпендикулярно векторам 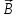 и и 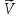 . В . В этот момент времени 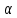 -частица будет двигаться по окружности радиуса -частица будет двигаться по окружности радиусаR= 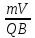 (2) (2)где Q= 3,2∙ 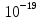 Кл - заряд Кл - заряд 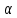 -частицы -частицыm= 6,65 ∙ 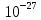 Кл - масса Кл - масса 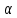 -частицы -частицыПолное ускорение 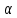 -частицы -частицыa=  (3) (3)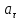 =0, т.к скорость движения по окружности постоянна =0, т.к скорость движения по окружности постоянна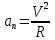 (4) (4)По условию задачи силы действующие со стороны полей противонаправлены. Результирующая сила, заставляющая 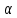 -частицу двигаться по окружности является центростремительной -частицу двигаться по окружности является центростремительной F= 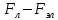 (5) (5)Сила Лоренца 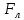 =QVB (6) =QVB (6)Сила, действующая со стороны электрического поля на 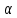 -частицу -частицу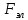 =QE (7) =QE (7)Из уравнений (5), (6) и (7) F=QVB-QE (8) Центробежная сила F= 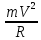 (9) (9)Из (8) и (9) 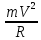 = QVB - QE = QVB - QEотсюда R= 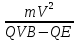 (10) (10)Из уравнений (3) и (4) с учетом того, что 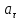 =0 получим =0 получим а= 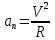 (11) (11)Из уравнений (11) и (10) определим ускорение 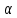 -частицы в начальной момент времени -частицы в начальной момент времени 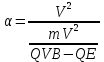 = = 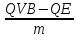 (12) (12)Подставим численные значения 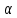 = = 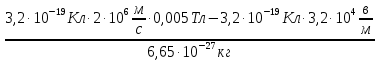 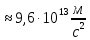 Ответ: 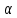 = =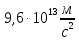 |
