ЭлмехППвСЭС, вариант 8. Решение Подготовка исходных данных

• Название: Решение Подготовка исходных данных
• Дата: 19.09.2021
• Размер: 0.85 Mb.
• Имя файла: ЭлмехППвСЭС, вариант 8.docx
• Тип: Задача; #233950

Электромеханические переходные процессы, вариант 8

Задача 1.На рисунке 1 приведена схема электрической системы, содержащая генераторную станцию и приемную систему бесконечной мощности. Известна передаваемая мощность Р_н, cos_н со стороны генераторной станции через трансформаторы Тр1, Тр2 и двухцепную линию электропередачи (ЛЭП). Определить запас устойчивости системы для случаев: а)при отсутствии АРВ; б)при АРВ пропорционального действия; в)при АРВ сильного действия.



Рисунок 1 - Схема электропередачи

Параметры схемы и параметры исходного режима:

Генератор Г: Р_н=500 МВА; cos_н=0,85; x_d=2,49; x^/ =0,37

Трансформатор Тр1 и Тр2: S_н=200 МВА; u_k=10,5%

Линия электропередачи (ЛЭП): U_сср=115кВ; L=120 км; х₀=0,4 Ом/км с тросом

Передаваемая мощность от генератора на шины системы: : Р_н0=450МВА; cos_н=0,9

Решение:

1. 
   Подготовка исходных данных
   

Расчет выполним в относительных единицах с приближенным приведением к основной ступени напряжения.

Примем за базисные условия S_б=500 МВА; U_б =115кВ.

Рассчитываем относительные сопротивления элементов.

Сопротивления генератора х_г:

-синхронное: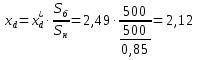



-переходное: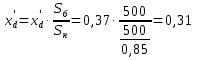



Сопротивление первого и второго трансформаторов:



Сопротивление линий:



Относительные значения передаваемой мощности от генератора на шины приемной системы:







Рисунок 2 - Схема замещения электропередачи

2. 
   Определение запасов устойчивости системы
   

а) при отсутствии АРВ предел передаваемой мощности определяется из условия постоянства синхронной ЭДС E_q = constпри х_г=х_dи U=1.

Суммарное сопротивление электропередачи Х_а равно:



Найдем синхронную ЭДС E_q: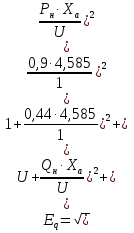



Предел передаваемой мощности:



Коэффициент запаса статической устойчивости:



б) при установке на генераторах АРВ пропорционального действия предел передаваемой мощности и устойчивости можно приближенно определить исходя из постоянства ЭДС E_q^’ за переходным сопротивлением .

Суммарное сопротивление электропередачи Х_б равно:



Найдем синхронную ЭДС :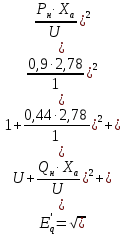



Предел передаваемой мощности:



Коэффициент запаса статической устойчивости:



в) АРВ сильного действия в зависимости от настройки может обеспечивать постоянство напряжения либо на выводах генератора, либо за трансформатором Тр1 в начале линии. Определим предел устойчивости, принимая напряжение генератора U_г=const. В этом случае сопротивление генератора принимается равным нулю.

Суммарное сопротивление электропередачи Х_в равно:



Найдем напряжение на выводах генератора: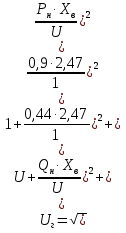



Предел передаваемой мощности:



Коэффициент запаса статической устойчивости:


Задача 2. Определить величину максимальной мощности, передаваемую станцией С₁, построить график зависимости Р₁=f(₁₂).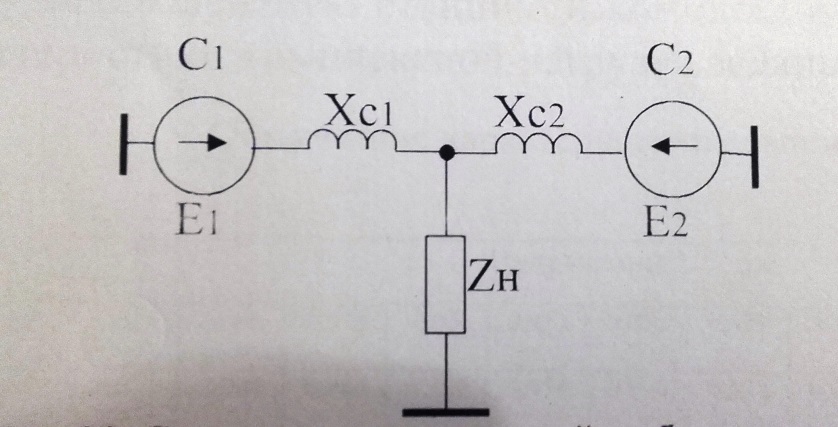



Рисунок 3- система из двух станций, работающая на нагрузку, которая задана постоянным сопротивлением

Исходные данные в относительных единицах:

Е₁ = 1,7; Е₂=1,2; х_с1=0,7; х_с2=0,9; z_н=1,2+j1,3

Если схема замещения между источниками состоит из активных и индуктивных сопротивлений, а нагрузка представлена постоянными сопротивлениями, которые не зависят от тока и напряжения, то ток и мощность передающей станции определяется через собственные и взаимные проводимости ветвей системы. Вычислив для передающей станции собственные и взаимные проводимости сразу можно записать зависимость Р₁=f(₁₂) в виде:



Максимум этой характеристики



дает значение действительного предела мощности.

Собственное и взаимное сопротивления для станции 1:



тогда ; ₁₁=83,3º; ₁₁=90^˚-₁₁=90^˚-83,3º=6,7º



тогда ; ₁₂=97,4º; ₁₂=90^˚-₁₂=90^˚-97,4º=-7,4º

Подставляя найденные значения в формулу для Р₁, получим:



или



Задаваясь значениями угла вычисляем значения Р₁. Результаты заносим в таблицу 1.

Зависимость ₁₂=f(Р₁)

Таблица 1

12, град	-7,4	0	30	60	90	120	150
Р1, о.е.	0,25	0,39	0,91	1,25	1,32	1,11	0,67

Максимум характеристики наблюдается в случаев, когда (₁₂+7,4˚)=90˚ при этом значение действительного предела активной мощности станции 1:



Угловая характеристика Р₁=f(₁₂), изображена на рисунке 4.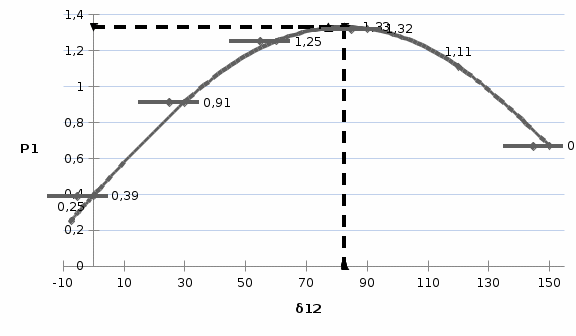



Рисунок 4-Угловая характеристика мощности генератора Г1

Задача 3.Мощный узел нагрузки, представленной схемой замещения на рис.5, содержит одну эквивалентную станцию и комплексную нагрузку. Статические типовые характеристики комплексной нагрузки заданы в таблице 2.

Исходные данные:

При относительном напряжении на шинах нагрузки U*=1, активная мощность нагрузки равна P_н0 = 0,5; реактивная Q_н0=0,8. Реактивное сопротивление системы x_с = 2,3. Напряжение U=110кВ.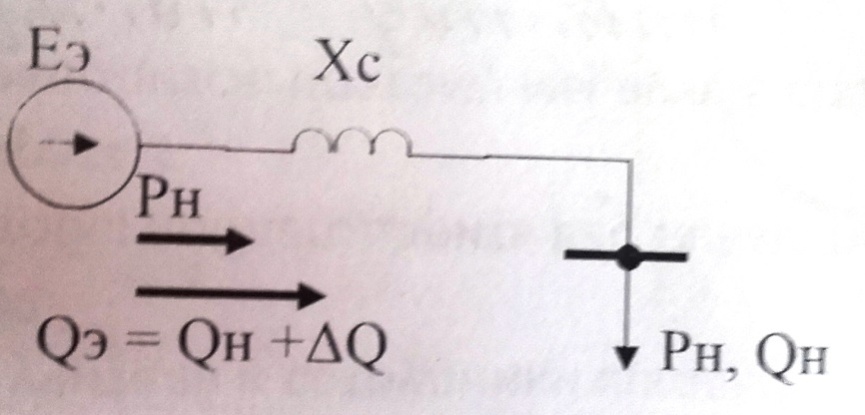



Рисунок 5 – Схема узла нагрузки

Требуется проверить устойчивость нагрузки указанной системы, построив зависимость E_э=f(U) и Q_э=f(U). При проверки воспользоваться критериями: dE_э/dU=0; dQ_э/dE=-

Статические характеристики комплексной нагрузки

Таблица 2

Мощность, о.е.	Напряжение U*, о.е.
	1,05	1,025	1,0	0,975	0,95	0,925	0,9	0,875	0,85	0,825	0,8	0,775	0,750
Активная, при напряжении 110 кВ; Pн0	1,033	1,017	1,0	0,984	0,969	0,954	0,941	0,928	0,916	0,904	0,898	0,882	0,872
Реактивная, при напряжении 110кВ; Qн0	1,090	1,045	1,0	0,962	0,930	0,905	0,885	0,870	0,858	0,849	0,844	0,844	0,848

Решение:

Мощностьнагрузки изменяется при изменении напряжения:P_н=P_н0Р^*; Q_н=Q_н0Q^*.

Эквивалентная ЭДС Е_э определяется по формуле: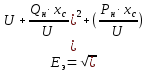



Реактивная мощность, «потребляемая» сопротивлением системы x_c:



Реактивная мощность, выдаваемая эквивалентной станцией: Q_э=Q_н+Q.

Задаваясь различными значениями напряжения U=U^*(в соответствии с таблицей статических характеристик комплексной нагрузки) можно определить величины P_н, Q_н, Е_э, Q, Q_э для различных напряжений. Результаты сведем в таблицу.

Результаты расчетов эквивалентной ЭДС Е_э и реактивной мощности Q_э:

U	1,05	1,025	1,0	0,975	0,95	0,925	0,9	0,875	0,85	0,825	0,8	0,775	0,750
Pн	0,517	0,509	0,5	0,492	0,485	0,477	0,471	0,464	0,458	0,452	0,449	0,441	0,436
Qн	0,872	0,836	0,8	0,770	0,744	0,724	0,708	0,696	0,686	0,679	0,675	0,675	0,678
	3,169	3,117	3,064	3,022	2,991	2,972	2,964	2,967	2,977	2,996	3,030	3,072	3,130
	2,362	2,202	2,047	1,919	1,813	1,729	1,662	1,609	1,566	1,531	1,512	1,496	1,496
Qэ	3,234	3,038	2,847	2,689	2,557	2,453	2,370	2,305	2,252	2,210	2,187	2,171	2,174

По полученным данным строим графики E_э=f(U) и Q_э=f(U).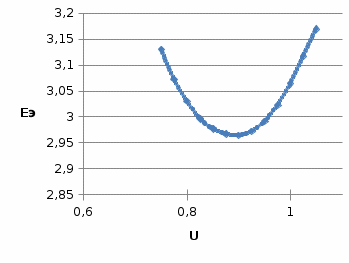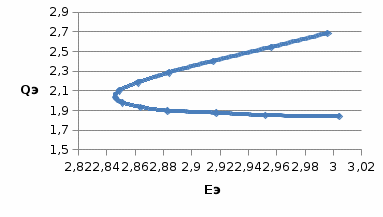



Рисунок 6- Определение критического напряжения и критической ЭДС
Задача 4. Станция работает через электропередачу на систему неограничеснной мощности и передает в систему мощность Р_н, cos_н (рисунок 7). Требуется: а)рассчитать и построить угловые характеристики активной мощности для исходного, аварийного и послеаварийного режимов; б)определить предельное время отключения трехфазного короткого замыкания, которое произошло на расстоянии L^’от начала одной из цепей ЛЭП.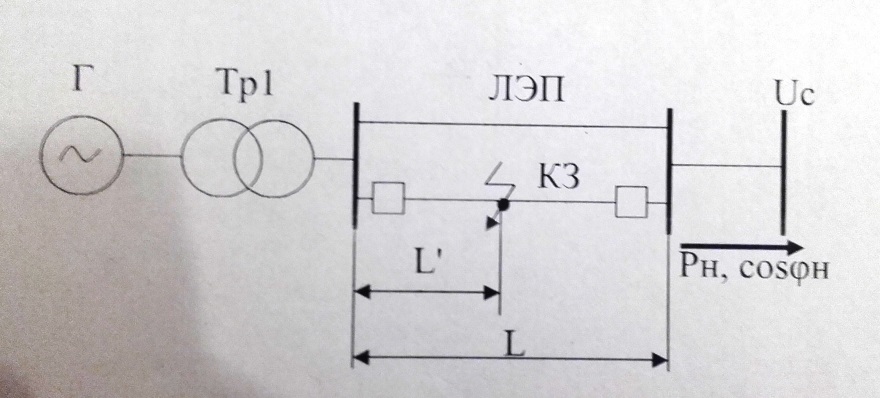



Рисунок 7- Схема электропередачи

Исходные данные:

Генератор: Р_нг=500 МВА; cos_н=0,85; U_нг=10,5кВ; x^/ =0,37; Т_j= 33 с

Трансформатор Тр: S_н=200 МВА; u_k= 10,5%; U_нв =121кВ; U_нн =13,8 кВ

Коэффициент трансформации:

ЛЭП: воздушная линия с тросом L=120 км; L^’= 0,2L; х₀=0,4 Ом/км

Система: U_сср=115кВ

Нагрузка: Р_н0=450 МВА; cos_н=0,9

Подготовка исходных данных

Расчет параметров элементов схем замещения будем вести в точных относительных единицах с учетом принятых базисных условий: S_б=500 МВА; U_б1 = 115кВ; U_б2 = U_б1/К_т = =13 кВ.

Генератор: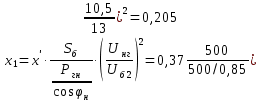





Трансформатор: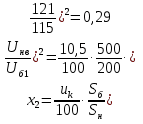



Линия: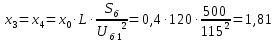







Система:



Нагрузка:




Активная нагрузка на генератор:



Режимы электропередачи

I-нормальный режим. Схема замещения нормального режима приведена на рис.8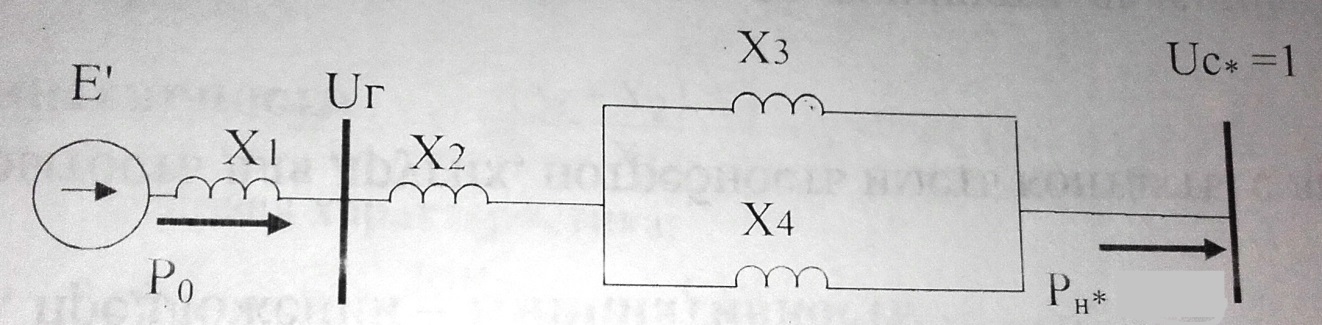



Рисунок 8-Схема замещения нормального режима электропередачи

Определим результирующее сопротивление электропередачи в нормальном режиме:



Переходная ЭДС генератора: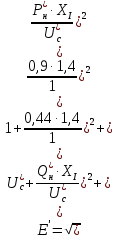



Угловая характеристика:



Амплитуда угловой характеристики:

P_Im=1,46

II- аварийный режим. Схема замещения аварийного режима приведена на рисунке 9.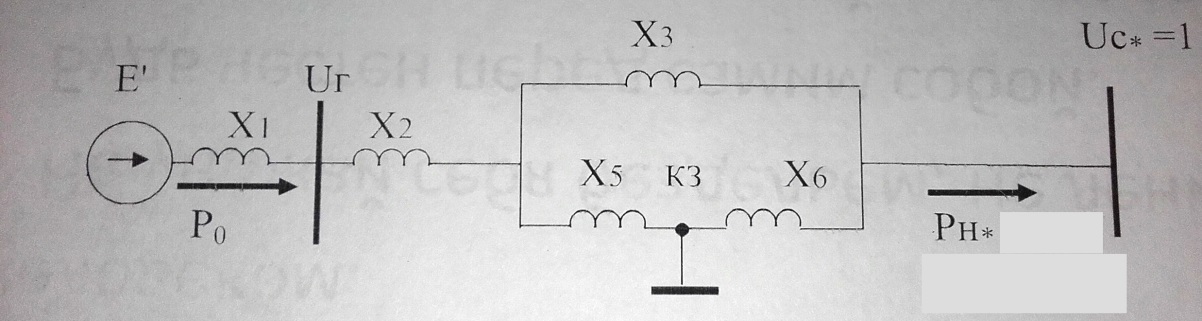



Рисунок 9 – Схема замещения аварийного режима электропередачи

Определим результирующее сопротивление электропередачи в аварийном режиме:

Следует учесть, что ветвь с сопротивлением х₆ не влияет на формирование угловой характеристики аварийного режима в связи с тем, что сопротивление х₆ включено между шинами системы бесконечной мощности и землей.

Тогда,



Угловая характеристика:



Амплитуда угловой характеристики:

P_IIm=0,43
III- послеаварийный режим. Схема замещения послеаварийного режима приведена на рисунке 10.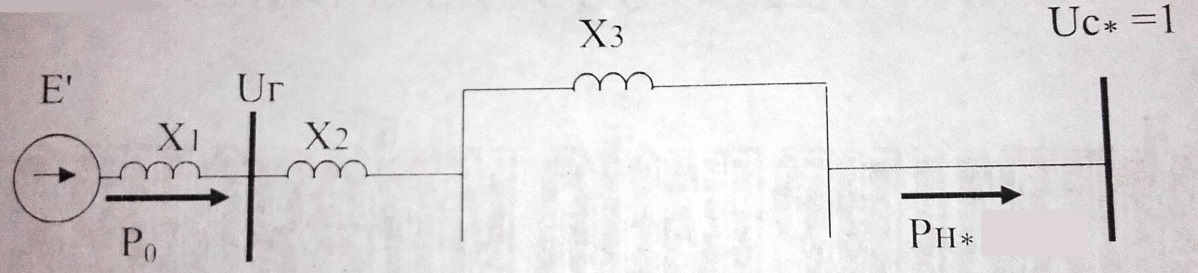



Рисунок 10 – Схема замещения послеаварийного режима электропередачи

Определим результирующее сопротивление электропередачи в послеаварийном режиме:



Угловая характеристика:



Амплитуда угловой характеристики:

P_Im=0,89

На рисунке 11 приведены угловые характеристики активной мощности всех режимов.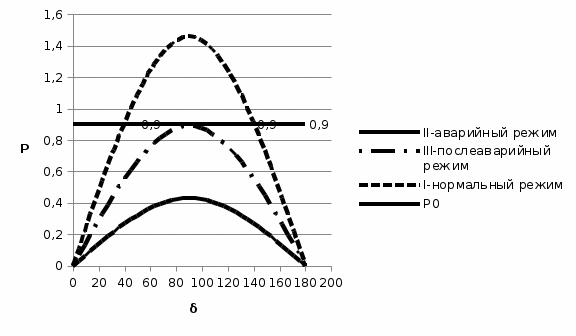



Рисунок 11 – Угловые характеристики активной мощности
Определение предельного угла отключения

Угол ₀ между переходной ЭДС Е^/ и напряжением системы в начальный момент возникновения КЗ:



Критический угол _кр:





Предельный угол отключения определяется по соотношению:





Тогда:



Получение зависимости =f(t)и определение времени t_отк, при котором достигается _отк

Используется метод последовательных интервалов. Примем продолжительность интервала t=0,05с.

Для использования в формулах расчета размерностей градусы и секунды, рассчитываем коэффициент k:



Начальные условия для интегрирования методов последовательных интервалов следующее: при t=0 ₍₀₎=₀=37,82˚

Небаланс между мощностью турбины и мощностью генератора при t=0, определяется по соотношению:



Проводится расчет интегралов.

Первый интеграл 0-0,05с.

Приращение угла ₍₁₎ в течение первого интервала времени:



Угол  в конце первого интервала:



Небаланс мощности при угле :



Второй интервал 0,05-0,1с.

Приращение угла ₍₂₎ в течение второго интервала времени:



Угол  в конце второго интервала:



Небаланс мощности при угле :



Третий интервал 0,1-0,15с.

Приращение угла ₍₃₎ в течение третьего интервала времени:



Угол  в конце третьего интервала:



Небаланс мощности при угле :



Расчеты продолжаются до тех пор, пока на некотором (k)-том интервале времени угол _к не превысит значения угла отключения _отк.

Результаты сводят в таблицу 4.

Результаты интегрирования методом последовательных интервалов

Таблица 4

t,с	d, град	DР, о.е.	Dd, град
0	37,82	0,636
0-0,05	38,19	0,634	0,37
0,05-0,1	39,29	0,628	1,10
0,1-0,15	41,13	0,617	1,83
0,15-0,2	43,68	0,603	2,55
0,2-0,25	46,92	0,586	3,25
0,25-0,3	50,85	0,567	3,93
0,3-0,35	55,44	0,546	4,59
0,35-0,4	60,66	0,526	5,22
0,4-0,45	66,49	0,504	5,83
0,45-0,5	72,90	0,489	6,41
0,5-0,55	79,88	0,479	6,98
0,55-0,6	87,42	0,470	7,54
0,6-0,65	95,5	0,472	8,08

Таким образом, предельное время отключения трехфазного к.з. находится в интервале 0,6-0,65 с, так как на этом интервале времени превышен угол _отк=88,8˚.

Для уточнения времени отключения строится по данным таблицы 4 зависимость =f(t) (рисунок 12).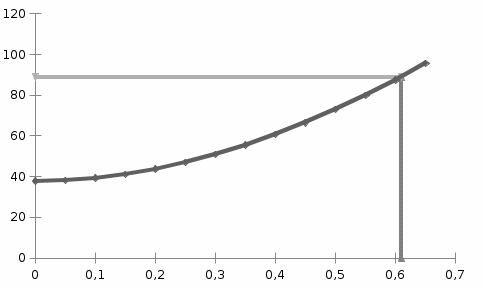



Рисунок 12- Уточнение предельного времени отключения трехфазного к.з.
В соответствии с графиком =f(t), приведенным на рисунке 12, предельное время отключения к.з. составляет t_отк=0,61с.