Навигация по странице:1. Расчет режима, предельного по статической апериодической устойчивости С УЧЕТОМ АРВ. Цель. Расчет режима, предельного по статической апериодической устойчивости с учетом АРВ.Метод деления пополам для поиска предельного установившегося режимаРезультаты расчета режима, предельного по статической апериодической устойчивости С УЧЕТОМ АРВРезультаты расчета. Динамика движения собственных чисел при утяжелении. С УЧЕТОМ АРВ.Результаты расчета. Динамика изменения напряжений ( U 1, U 2, U 3) при утяжелении. С УЧЕТОМ АРВ.Результаты расчета. Динамика изменения углов ( delta 1, delta 2, delta 3) при утяжелении. С УЧЕТОМ АРВ.2. Расчет режима, предельного по статической устойчивости БЕЗ УЧЕТА АРВ. Цель. Расчет режима, предельного по статической устойчивости БЕЗ УЧЕТА АРВ.Используя метод деления пополам, рассчитать режим, предельный по статической устойчивости. Проанализировать полученные результаты. Efd 0 G 1 и Efd 0Результаты расчета режима, предельного по статической устойчивости БЕЗ УЧЕТА АРВРезультаты расчета. Динамика движения собственных чисел при утяжелении. БЕЗ УЧЕТА АРВ.Результаты расчета. Динамика изменения напряжения при утяжелении. БЕЗ УЧЕТА АРВ.Результаты расчета. Динамика изменения угла при утяжелении. БЕЗ УЧЕТА АРВ.3. Расчет динамики при нарушении статической устойчивости. С УЧЕТОМ АРВ. Цель. Расчет динамики при нарушении статической устойчивости С УЧЕТОМ АРВ.Задача. Утяжелить предельный режим в динамике. Получить статическую неустойчивость. Проанализировать полученные результаты. Построить динамику изменения переменных состояния.Последовательность действийВеличина предельной мощности Pпред=0.79766; величина изменения мощности, приводящая к статической неустойчивости Pпред+dP=0.879914. Расчет динамики при нарушении статической устойчивости. БЕЗ УЧЕТА АРВ. Цель. Расчет динамики при нарушении статической устойчивости БЕЗ УЧЕТА АРВ.Результаты расчета переменных состояния БЕЗ УЧЕТА АРВ.
|
В результате проведенных расчетов ошибочно делать вывод о том, что установка арв отрицательно влияет на предел по статической устойчивости! На предел по статической устойчивости отрицательно влияет неправильная настройка арв, а не его наличие!
В результате проведенных расчетов ошибочно делать вывод о том, что установка АРВ отрицательно влияет на предел по статической устойчивости! На предел по статической устойчивости отрицательно влияет неправильная настройка АРВ, а не его наличие!
Исходные данные. Вариант№ 69 Дубовик3:
Обозначение
|
Значение
|
Примечание
|
M0G1
|
1.3
|
инерция первого агрегата
|
M0G2
|
1
|
инерция второго агрегата
|
D0G1
|
0.2
|
коэффициент демпфирования первого агрегата
|
D0G2
|
0.2
|
коэффициент демпфирования второго агрегата
|
XG1
|
0.2
|
реактивное сопротивление первого генератора
|
XG2
|
0.3
|
реактивное сопротивление второго генератора
|
XL
|
1
|
реактивное сопротивление линии
|
V4
|
0.9
|
Модуль напряжения ШБМ
|
Pm0
|
0.5
|
Начальная суммарная механическая мощность станции (НАЧИНАТЬ РАСЧЕТ С ДАННОЙ МОЩНОСТИ!)
|
K
|
0.4
|
Коэффициент распределения мощности между агрегатами (Pm0G1=K*Pm0 Pm0G2=(1-K)*Pm0)
|
Pm0G1
|
0.2
|
Начальная механическая мощность первого генератора
|
Pm0G2
|
0.3
|
Начальная механическая мощность второго генератора
|
Efd0G1
|
1
|
Efd0 первого генератора
|
Efd0G2
|
0.9
|
Efd0 второго генератора
|
XkomG1
|
0.05
|
коэффициент компаундирования первого генератора
|
XkomG2
|
0.02
|
коэффициент компаундирования второго генератора
|
KpG1
|
82
|
коэффициент усиления пропорционального звена АРВ первого генератора
|
KpG2
|
23
|
коэффициент усиления пропорционального звена АРВ второго генератора
|
KdG1
|
14
|
коэффициент усиления дифференциального звена АРВ первого генератора
|
KdG2
|
16
|
коэффициент усиления дифференциального звена АРВ второго генератора
|
TdG1
|
0.05
|
постоянная времени дифференциального звена АРВ первого генератора
|
TdG2
|
0.01
|
постоянная времени дифференциального звена АРВ второго генератора
|
TvG1
|
0.4
|
постоянная времени возбудителя первого генератора
|
TvG2
|
0.7
|
постоянная времени возбудителя второго генератора
|
VrefG1
|
1
|
уставка АРВ первого генератора
|
VrefG2
|
1
|
уставка АРВ второго генератора
|
1. Расчет режима, предельного по статической апериодической устойчивости С УЧЕТОМ АРВ.
Цель. Расчет режима, предельного по статической апериодической устойчивости с учетом АРВ.
Используя метод деления пополам, рассчитать режим, предельный по статической апериодической устойчивости. Проанализировать полученные результаты.
Для рассматриваемой системы станция – ШБМ предел по статической устойчивости с учетом действия АРВ в общем случае не совпадает с пределом по существованию установившегося режима. Необходимое, но недостаточнео условие - должно существовать решение системы нелинейных алгебраических уравнений (должен существовать установившийся режим). Достаточное условие - наличие минимального числа собственных чисел с положительной действительной частью.
Метод деления пополам для поиска предельного установившегося режима:
Задаем P0 (см. вариант) – исходное значение генерируемой мощности и dP – исходный шаг.
Шаг1. рассчитываем установившийся режим для P1=P0+dP.
Если режим (решение) существует, то находим собственные числа.
Если режим (решение) существует и отсутствуют собственные числа с положительной действительной частью, то P0=P1.
Если режим (решение) НЕ существует, либо имеется хотя бы одно собственное число с положительной действительной частью, то dP=dP/2.
Шаг3. Если dP<0.001, при этом установившийся режим существует и отсутствуют собственные числа с положительной действительной частью, то завершаем расчет, иначе переходим к шагу 1.
Результаты расчета режима, предельного по статической апериодической устойчивости С УЧЕТОМ АРВ:
P1
|
dP
|
U1
|
delta1
|
U2
|
delta2
|
U3
|
delta3
|
eig1
|
eig2
|
eig3
|
eig4
|
eig5
|
eig6
|
eig7
|
eig8
|
Устойчива? 1/0
|
0.5
|
0.1
|
0.99221
|
34.0502
|
1.0546
|
36.2409
|
0.9782
|
39.3707
|
-1314.123
|
-120.761
|
-0.089+1.907i
|
-0.089-1.907i
|
-0.087+0.534i
|
-0.087-0.534i
|
-4.357
|
-1.421
|
1
|
0.6
|
0.1
|
0.99069
|
42.2939
|
1.0809
|
44.8631
|
0.96102
|
48.8074
|
-1323.389
|
-110.708
|
-4.341
|
-0.088+1.921i
|
-0.088-1.921i
|
-0.087+0.505i
|
-0.087-0.505i
|
-1.422
|
1
|
0.7
|
0.1
|
0.98922
|
51.8369
|
1.1228
|
54.7269
|
0.93001
|
59.7088
|
-1335.707
|
-97.36
|
-4.313
|
-0.086+1.94i
|
-0.086-1.94i
|
-0.088+0.462i
|
-0.088-0.462i
|
-1.422
|
1
|
0.8
|
0.1
|
0.98416
|
64.5815
|
0.97241
|
68.416
|
1.1937
|
71.6223
|
-1373.305
|
20.826
|
-5.269
|
-0.195+2.566i
|
-0.195-2.566i
|
-0.087+0.38i
|
-0.087-0.38i
|
-1.408
|
0
|
0.75
|
0.05
|
0.98874
|
57.4392
|
1.155
|
60.4509
|
0.90376
|
66.1285
|
-1343.525
|
-88.864
|
-4.292
|
-0.085+1.953i
|
-0.085-1.953i
|
-0.088+0.431i
|
-0.088-0.431i
|
-1.422
|
1
|
0.8
|
0.05
|
0.98416
|
64.5815
|
0.97241
|
68.416
|
1.1937
|
71.6223
|
-1373.305
|
20.826
|
-5.269
|
-0.195+2.566i
|
-0.195-2.566i
|
-0.087+0.38i
|
-0.087-0.38i
|
-1.408
|
0
|
0.775
|
0.025
|
0.98869
|
60.571
|
1.1761
|
63.6273
|
0.88557
|
69.7388
|
-1348.023
|
-83.946
|
-4.277
|
-0.084+1.961i
|
-0.084-1.961i
|
-0.088+0.413i
|
-0.088-0.413i
|
-1.423
|
1
|
0.8
|
0.025
|
0.98416
|
64.5815
|
0.97241
|
68.416
|
1.1937
|
71.6223
|
-1373.305
|
20.826
|
-5.269
|
-0.195+2.566i
|
-0.195-2.566i
|
-0.087+0.38i
|
-0.087-0.38i
|
-1.408
|
0
|
0.7875
|
0.0125
|
0.98874
|
62.2477
|
1.1885
|
65.3207
|
0.8746
|
71.6822
|
-1350.458
|
-81.271
|
-4.269
|
-0.083+1.965i
|
-0.083-1.965i
|
-0.088+0.402i
|
-0.088-0.402i
|
-1.423
|
1
|
0.8
|
0.0125
|
0.98416
|
64.5815
|
0.97241
|
68.416
|
1.1937
|
71.6223
|
-1373.305
|
20.826
|
-5.269
|
-0.195+2.566i
|
-0.195-2.566i
|
-0.087+0.38i
|
-0.087-0.38i
|
-1.408
|
0
|
0.79375
|
0.00625
|
0.98879
|
63.1188
|
1.1953
|
66.1986
|
0.86852
|
72.6957
|
-1351.728
|
-79.87
|
-4.264
|
-0.083+1.968i
|
-0.083-1.968i
|
-0.088+0.396i
|
-0.088-0.396i
|
-1.423
|
1
|
0.8
|
0.00625
|
0.98416
|
64.5815
|
0.97241
|
68.416
|
1.1937
|
71.6223
|
-1373.305
|
20.826
|
-5.269
|
-0.195+2.566i
|
-0.195-2.566i
|
-0.087+0.38i
|
-0.087-0.38i
|
-1.408
|
0
|
0.79688
|
0.003125
|
0.98882
|
63.5634
|
1.1989
|
66.6461
|
0.86531
|
73.214
|
-1352.377
|
-79.152
|
-4.261
|
-0.082+1.969i
|
-0.082-1.969i
|
-0.088+0.393i
|
-0.088-0.393i
|
-1.423
|
1
|
0.8
|
0.003125
|
0.98416
|
64.5815
|
0.97241
|
68.416
|
1.1937
|
71.6223
|
-1373.305
|
20.826
|
-5.269
|
-0.195+2.566i
|
-0.195-2.566i
|
-0.087+0.38i
|
-0.087-0.38i
|
-1.408
|
0
|
0.79844
|
0.0015625
|
0.98427
|
64.333
|
0.97324
|
68.1563
|
1.1917
|
71.3711
|
-1373.286
|
21.616
|
-5.247
|
-0.188+2.546i
|
-0.188-2.546i
|
-0.087+0.382i
|
-0.087-0.382i
|
-1.408
|
0
|
0.79766
|
0.00078125
|
0.98883
|
63.6756
|
1.1998
|
66.7589
|
0.86449
|
73.3448
|
-1352.54
|
-78.97
|
-4.261
|
-0.082+1.969i
|
-0.082-1.969i
|
-0.088+0.392i
|
-0.088-0.392i
|
-1.423
|
1
|
Результаты расчета. Динамика движения собственных чисел при утяжелении. С УЧЕТОМ АРВ.
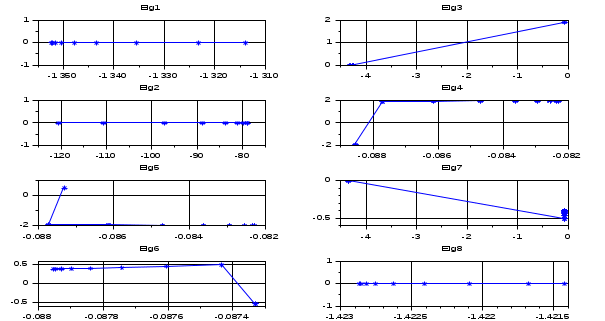
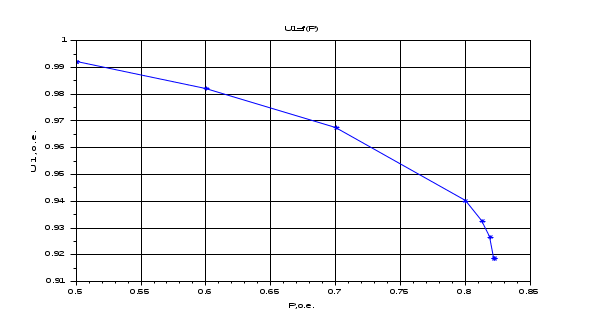
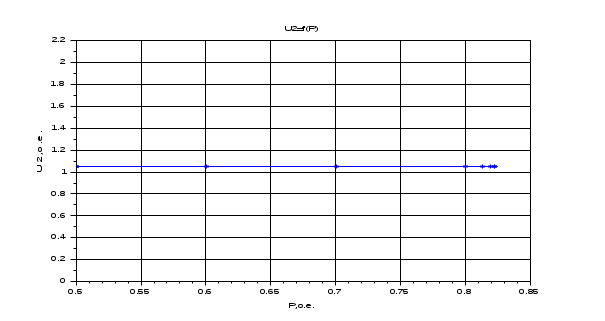
Результаты расчета. Динамика изменения напряжений (U1, U2, U3) при утяжелении. С УЧЕТОМ АРВ.
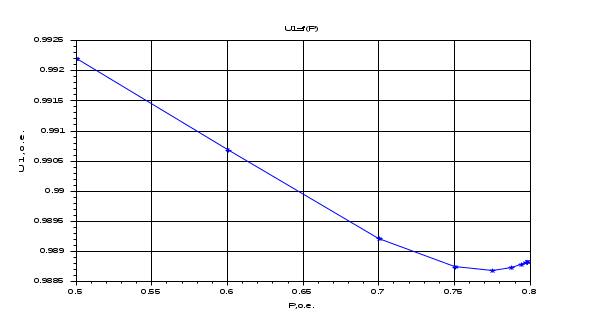
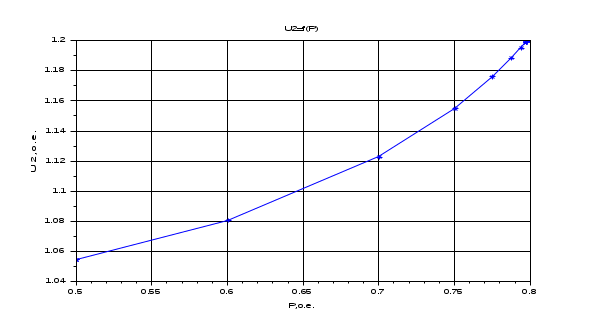
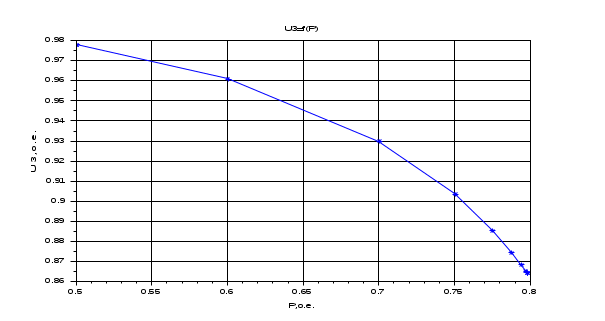
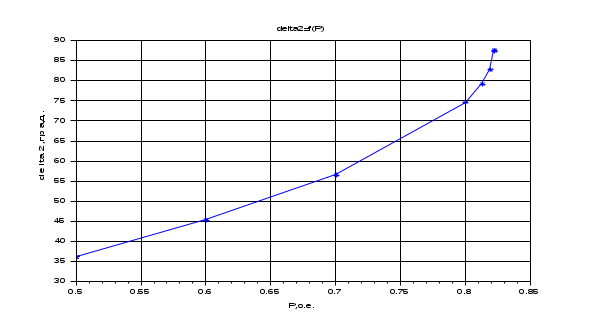
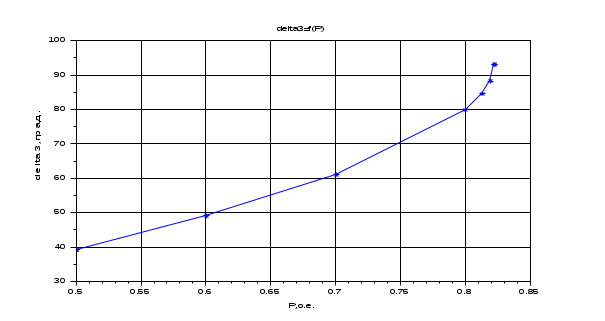
Результаты расчета. Динамика изменения углов (delta1, delta2, delta3) при утяжелении. С УЧЕТОМ АРВ.
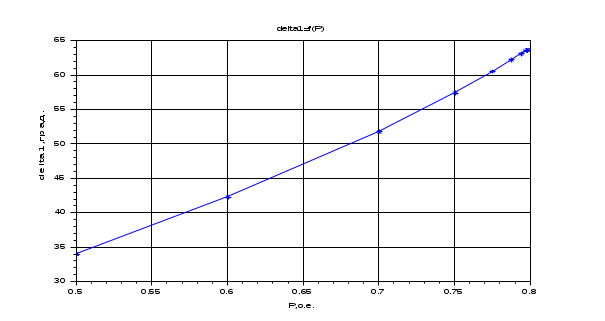
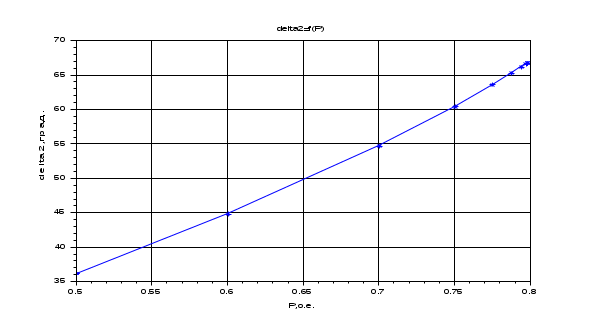
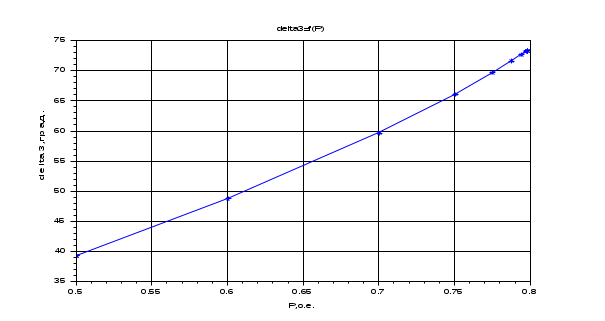
2. Расчет режима, предельного по статической устойчивости БЕЗ УЧЕТА АРВ.
Цель. Расчет режима, предельного по статической устойчивости БЕЗ УЧЕТА АРВ.
Используя метод деления пополам, рассчитать режим, предельный по статической устойчивости. Проанализировать полученные результаты.
Efd0G1 и Efd0G2 на первом шаге утяжеления без АРВ должны соответствовать напряжениям U2 и U3 на первом шаге утяжеления с АРВ.
Для рассматриваемой системы станция – ШБМ предел по статической устойчивости без учета действия АРВ совпадает с пределом по существованию установившегося режима. Однако необходимо выполнять проверку как существования режима, так и отсутствия собственных чисел с положительной действительной частью. Необходимое, но недостаточнео условие - должно существовать решение системы нелинейных алгебраических уравнений (должен существовать установившийся режим). Достаточное условие - наличие минимального числа собственных чисел с положительной действительной частью.
Метод деления пополам для поиска предельного установившегося режима:
Задаем P0 (см. вариант) – исходное значение генерируемой мощности и dP – исходный шаг.
Шаг1. рассчитываем установившийся режим для P1=P0+dP.
Если режим (решение) существует, то находим собственные числа.
Если режим (решение) существует и отсутствуют собственные числа с положительной действительной частью, то P0=P1.
Если режим (решение) НЕ существует, либо имеется хотя бы одно собственное число с положительной действительной частью, то dP=dP/2.
Шаг3. Если dP<0.001, при этом установившийся режим существует и отсутствуют собственные числа с положительной действительной частью, то завершаем расчет, иначе переходим к шагу 1.
Результаты расчета режима, предельного по статической устойчивости БЕЗ УЧЕТА АРВ:
P1
|
dP
|
U1
|
delta1
|
U2
|
delta2
|
U3
|
delta3
|
eig1
|
eig2
|
eig3
|
eig4
|
eig5
|
eig6
|
eig7
|
eig8
|
Устойчива? 1/0
|
0.5
|
0.1
|
0.99221
|
34.0502
|
1.0546
|
36.2409
|
0.9782
|
39.3707
|
-20
|
-100
|
-0.09+1.876i
|
-0.09-1.876i
|
-0.087+0.525i
|
-0.087-0.525i
|
-2.5
|
-1.429
|
1
|
0.6
|
0.1
|
0.98223
|
42.7445
|
1.0546
|
45.4004
|
0.9782
|
49.1984
|
-20
|
-100
|
-0.09+1.865i
|
-0.09-1.865i
|
-0.087+0.486i
|
-0.087-0.486i
|
-2.5
|
-1.429
|
1
|
0.7
|
0.1
|
0.96764
|
53.4935
|
1.0546
|
56.6392
|
0.9782
|
61.1431
|
-20
|
-100
|
-0.09+1.849i
|
-0.09-1.849i
|
-0.087+0.424i
|
-0.087-0.424i
|
-2.5
|
-1.429
|
1
|
0.8
|
0.1
|
0.94016
|
70.9914
|
1.0546
|
74.6922
|
0.9782
|
79.9997
|
-20
|
-100
|
-0.09+1.82i
|
-0.09-1.82i
|
-0.087+0.273i
|
-0.087-0.273i
|
-2.5
|
-1.429
|
1
|
0.9
|
0.1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.85
|
0.05
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.825
|
0.025
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.8125
|
0.0125
|
0.93272
|
75.4426
|
1.0546
|
79.2314
|
0.9782
|
84.6665
|
-20
|
-100
|
-0.09+1.812i
|
-0.09-1.812i
|
-0.087+0.215i
|
-0.087-0.215i
|
-2.5
|
-1.429
|
1
|
0.825
|
0.0125
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.81875
|
0.00625
|
0.92668
|
79.0208
|
1.0546
|
82.8637
|
0.9782
|
88.3774
|
-20
|
-100
|
-0.09+1.806i
|
-0.09-1.806i
|
-0.087+0.154i
|
-0.087-0.154i
|
-2.5
|
-1.429
|
1
|
0.825
|
0.00625
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82187
|
0.003125
|
0.91892
|
83.6008
|
1.0546
|
87.491
|
0.9782
|
93.0735
|
-20
|
-100
|
-0.09+1.798i
|
-0.09-1.798i
|
-0.014
|
-0.16
|
-2.5
|
-1.429
|
1
|
0.825
|
0.003125
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82344
|
0.0015625
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82266
|
0.00078125
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82227
|
0.00039063
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82207
|
0.00019531
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82197
|
9.7656e-05
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82192
|
4.8828e-05
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.8219
|
2.4414e-05
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0.82189
|
1.2207e-05
|
0.91862
|
83.7774
|
1.0546
|
87.669
|
0.9782
|
93.2534
|
-20
|
-100
|
-0.09+1.798i
|
-0.09-1.798i
|
-0.007
|
-0.167
|
-2.5
|
-1.429
|
1
|
Результаты расчета. Динамика движения собственных чисел при утяжелении. БЕЗ УЧЕТА АРВ.
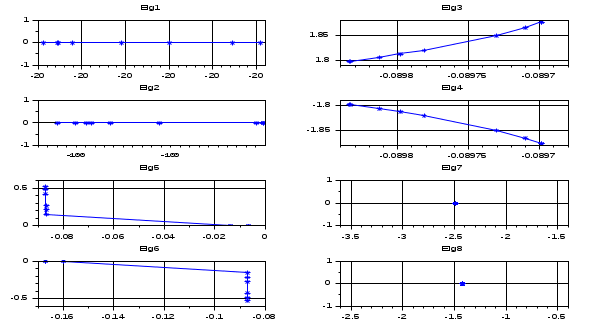
Результаты расчета. Динамика изменения напряжения при утяжелении. БЕЗ УЧЕТА АРВ.
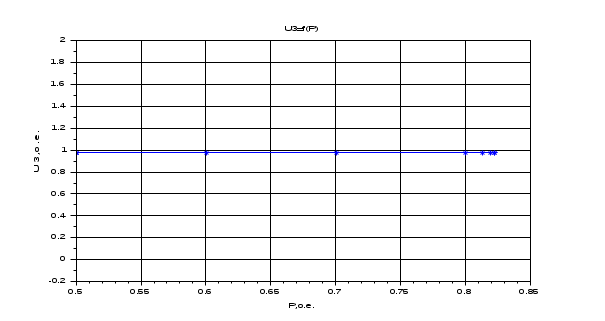
Результаты расчета. Динамика изменения угла при утяжелении. БЕЗ УЧЕТА АРВ.
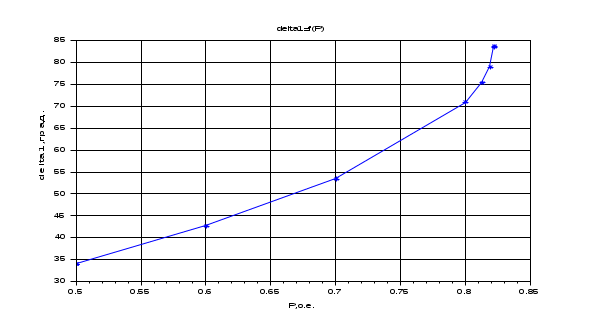
3. Расчет динамики при нарушении статической устойчивости. С УЧЕТОМ АРВ.
Цель. Расчет динамики при нарушении статической устойчивости С УЧЕТОМ АРВ.
Задача. Утяжелить предельный режим в динамике. Получить статическую неустойчивость. Проанализировать полученные результаты. Построить динамику изменения переменных состояния.
Последовательность действий:
1. Начинаем расчет динамики с рассчитанного предельного установившегося режима С УЧЕТОМ АРВ.
2. В момент времени t>10 незначительно увеличиваем передаваемую мощность.
3. Увеличение передаваемой мощности должно привести к возникновению статической неустойчивости.
Величина предельной мощности Pпред=0.79766; величина изменения мощности, приводящая к статической неустойчивости Pпред+dP=0.87991
Результаты расчета переменных состояния при нарушении статической устойчивости С УЧЕТОМ АРВ.
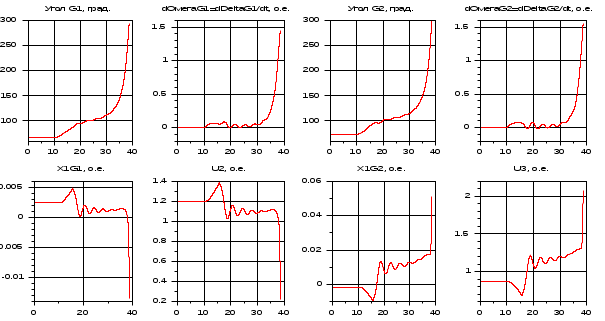
4. Расчет динамики при нарушении статической устойчивости. БЕЗ УЧЕТА АРВ.
Цель. Расчет динамики при нарушении статической устойчивости БЕЗ УЧЕТА АРВ.
Задача. Утяжелить предельный режим в динамике. Получить статическую неустойчивость. Проанализировать полученные результаты. Построить динамику изменения переменных состояния.
Последовательность действий:
1. Начинаем расчет динамики с рассчитанного предельного установившегося режима БЕЗ УЧЕТА АРВ.
2. В момент времени t>10 незначительно увеличиваем передаваемую мощность.
3. Увеличение передаваемой мощности должно привести к возникновению статической неустойчивости.
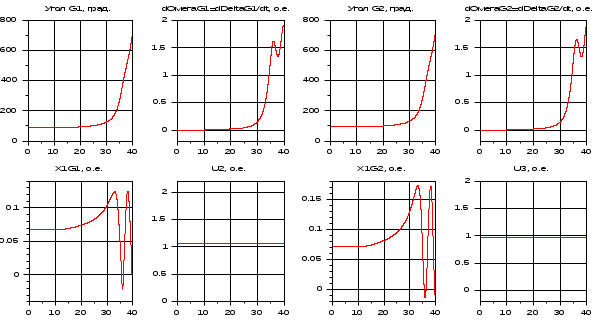
Результаты расчета переменных состояния БЕЗ УЧЕТА АРВ.
|
|
|
 Скачать 186.45 Kb.
Скачать 186.45 Kb.















