высшая математика 1 курс векорная алгебра. Решение задач тема 3 математика. Решение Прямая, проходящая через точки a 1 (x 1 y 1 ) и a 2 (x 2 y 2 ), представляется уравнениями
 Скачать 28.05 Kb. Скачать 28.05 Kb.
|
|
Задача 1. Даны координаты вершин треугольника АВС. Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла А, найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам А(1; 3) В(-2; 4) С(-3; 1) Решение: Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: 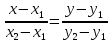 Уравнение прямой AB Каноническое уравнение прямой: 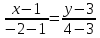 или 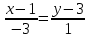 или y = -1/3x + 10/3 или 3y + x - 10 = 0 Уравнение прямой AC Каноническое уравнение прямой: 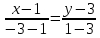 или 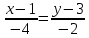 или y = 1/2x + 5/2 или 2y -x - 5 = 0 Уравнение прямой BC Каноническое уравнение прямой: 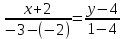 или 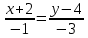 или y = 3x + 10 или y -3x - 10 = 0 Уравнение медианы треугольника Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 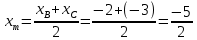 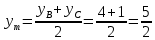 M(-5/2;5/2) Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(1;3) и М(-5/2;5/2), поэтому: Каноническое уравнение прямой: 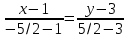 или 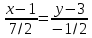 или y = 1/7x + 20/7 или 7y -x - 20 = 0 Найдем длину медианы. Расстояние между двумя точками выражается через координаты формулой: 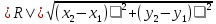 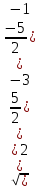 Уравнение высоты через вершину A Прямая, проходящая через точку А(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 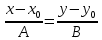 Найдем уравнение высоты через вершину A 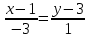 y = -1/3x + 10/3 или 3y +x -10 = 0 Длина высоты треугольника, проведенной из вершины A Расстояние d от точки А(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины: 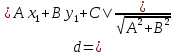 Найдем расстояние между точкой A(1;3) и прямой BC (y -3x - 10 = 0) 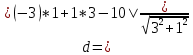 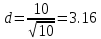 Уравнение биссектрисы треугольника Найдем биссектрису угла A. Известно, что диагонали ромба делят углы пополам. Найдем орты векторов AB(-3,1) и AC(-4,-2). Соответственно и на них, как на сторонах, построим ромб, диагональ которого AK, равную сумме ортов, можно взять в качестве направляющего вектора биссектрисы. 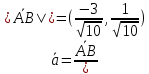 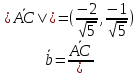 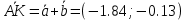 Каноническое уравнение биссектрисы AK примет вид: 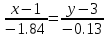 y = 0.071x + 2.93 или 1.84y - 0.13x -5.39 = 0 Длина биссектрисы Для нахождения длины биссектрисы данного угла треугольника воспользуемся тем, что она делит противоположную сторону треугольника на части пропорциональные сторонам треугольника, образующим этот угол, т.е. в нашем случае, если K - точка пересечения биссектрисы угла B со стороной BC. 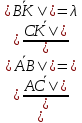 Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:  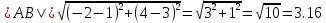 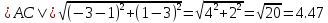 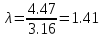 Поэтому 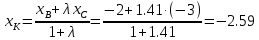 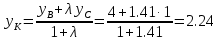 Итак, A(1,3) и K(-2.59;2.24). 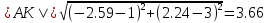 Уравнение параллельной прямой AB, проходящей через точку С(-3,1) Уравнение прямой AB: y = -1/3x + 10/3 Уравнение CL параллельно AB находится по формуле: y - y0 = k(x - x0) Подставляя x0 = -3, k = -1/3, y0 = 1 получим: y-1 = -1/3(x-(-3)) или y = -1/3x или 3y + x - 0 = 0 Уравнение параллельной прямой AC, проходящей через точку В (-2,4) Уравнение прямой AC: y = 1/2x + 5/2 Уравнение BN параллельно AC находится по формуле: y - y0 = k(x - x0) Подставляя x0 = -2, k = 1/2, y0 = 4 получим: y-4 = 1/2(x-(-2)) или y = 1/2x + 5 или 2y -x - 10 = 0 Уравнение параллельной прямой BC, проходящей через точку A(1,3) Уравнение прямой BC: y = 3x + 10 Уравнение AT параллельно BC находится по формуле: y - y0 = k(x - x0) Подставляя x0 = 1, k = 3, y0 = 3 получим: y-3 = 3(x-1) или y = 3x или y -3x - 0 = 0 Задача 2. По координатам вершин пирамиды АВСD средствами векторной алгебры найти: 1) длины ребер АВ и АС; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) проекцию вектора на 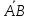 и и 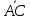 ; ; 5) объем пирамиды. А(2; 4; -6) В(1; 3; 5) С(0; -3; 8) D(3; 2; 3) Решение: 1) Координаты векторов. Координаты векторов находим по формуле: X = xj - xi; Y = yj - yi; Z = zj - zi здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj; Например, для вектора AB X = x2 - x1; Y = y2 - y1; Z = z2 - z1 X = 1-2; Y = 3-4; Z = 5-(-6) 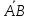 (-1;-1;11) (-1;-1;11)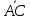 (-2;-7;14) (-2;-7;14)Длина вектора a(X;Y;Z) выражается через его координаты формулой: 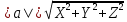 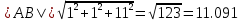 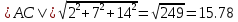 2) Угол между ребрами. Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле: 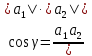 где a1a2 = X1X2 + Y1Y2 + Z1Z2 Найдем угол между ребрами 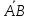 (-1;-1;11) и (-1;-1;11) и 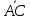 (-2;-7;14) (-2;-7;14)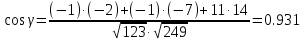 γ = arccos(0.931) = 21.3470 3) площадь грани АВС; Площадь грани можно найти по формуле: 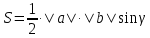 где 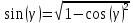 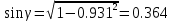 Площадь грани ABC 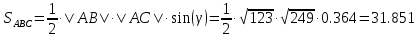 4) проекцию вектора на 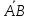 и и 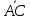 ; ;Проекцию вектора b на вектор a можно найти по формуле: 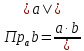 Найдем проекцию вектора AB на вектор AC 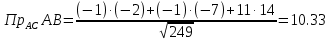 5) объем пирамиды. Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен: 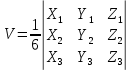 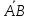 (-1;-1;11) (-1;-1;11)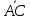 (-2;-7;14) (-2;-7;14)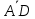 (1;-2;9) (1;-2;9)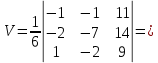 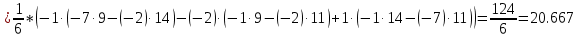 |
