Эксплуатационная прочность судов. отчет москаленко. Решение Пункт 1 Исходные данные представлены на Рисунке 1, а

• Название: Решение Пункт 1 Исходные данные представлены на Рисунке 1, а
• Анкор: Эксплуатационная прочность судов
• Дата: 08.03.2023
• Размер: 409.35 Kb.
• Имя файла: отчет москаленко.docx
• Тип: Документы; #974638

Федеральное Государственное Бюджетное Общеобразовательное Учреждение Высшего Образования

«Калининградский Государственный Технический Университет»
Кафедра Кораблестроения

Практическое задание №1

по дисциплине “Эксплуатационная прочность судов”

Вариант 06

Выполнила студентка группы 18–КС

факультета «Судостроения и энергетики»

Москаленко Ю.В.

Проверил д.т.н., профессор

Сутырин В.И.

г. Калининград

2022

Постановка задачи:

1. Определить положение главной центральной оси Ус, момент инерции Jz и моменты сопротивления Wz(1,2), соответствующие верхнему и нижнему крайнему волокну сечения.

2. Определить опасное сечение балки с учетом точки приложения и величины внешней силы

3. Определить нормальные, касательные и эквивалентные напряжения в точках 0.1.2.3 наиболее опасного поперечного сечения балки. Определить наиболее опасные точки в наиболее опасном сечении балки

4. Учитывая, что нормальные и касательные напряжения в опасной точке линейно зависят от внешней нагрузки, построить график зависимости эквивалентных напряжений от величины силы P.

5. Определить допустимую нагрузку Pкр, при которой эквивалентные напряжения в опасной точке достигнут величины допускаемых напряжений, равной 320 МПа.
Решение:

Пункт 1:

Исходные данные представлены на Рисунке 1, а.

1.1 Определим центр тяжести сечения. Для этого сложная фигура разбивается на простейшие с легко определяемыми центрами их тяжести, через которые проводятся центральные оси z_i и y_i, параллельные вспомогательным осям Z и Y (рис 1,б). В нашем случае рассматриваемое сечение разбивается на 2 прямоугольника, тогда:

• 
  Для верхнего прямоугольника: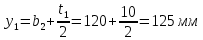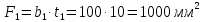
  

• 
  Для бокового прямоугольника: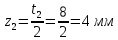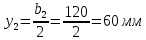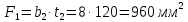
  

1.2 Определяем положение центра тяжести поперечного сечения: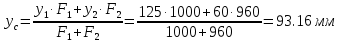






100

б)

а)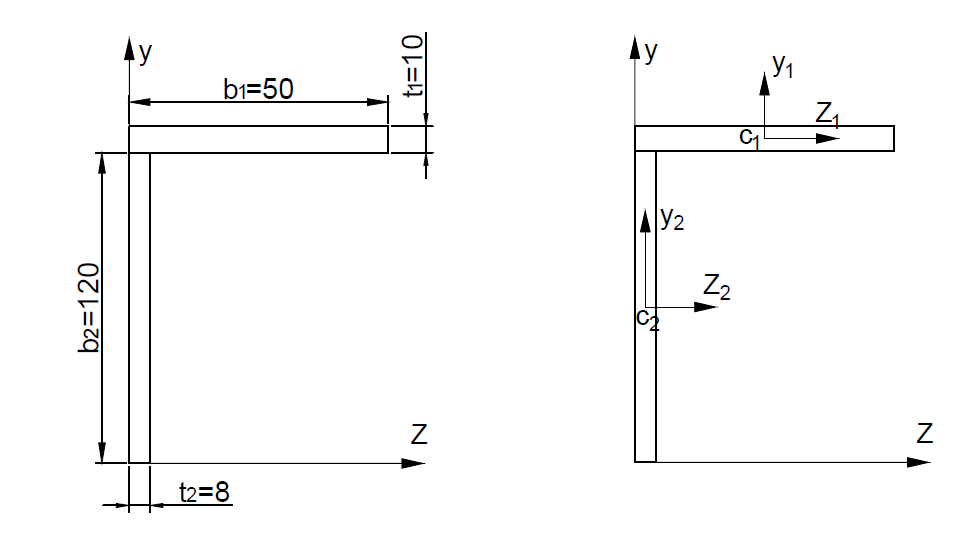

Рисунок 1

1.3 Определение моментов инерции относительно собственных центральных осей z_i и y_i.

Для прямоугольных сечений: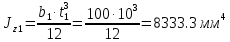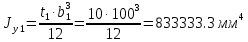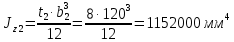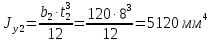









1.4 Проводим через центр тяжести сечения центральные оси z_с и y_с , параллельные вспомогательным осям Z и Y (рис 1,в).

1.5 Определение моментов инерции всего сечения относительно центральных осей z_с и y_с.

Осевые моменты инерции: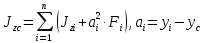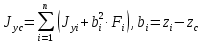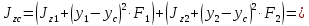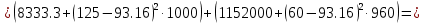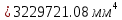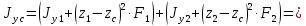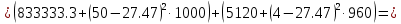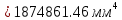

















1.6 Определение центробежного момента инерции.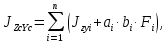



Если оси У и Z провести через центр тяжести прямоугольного сечения, то центробежный момент инерции равен нулю, так как эти оси совпадают с осями симметрии. Тогда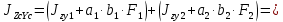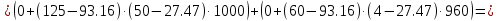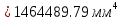







1.7 Определение главных моментов инерции относительно центральных осей.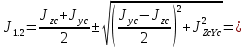









1.8 Определяем положение главных центральных осей.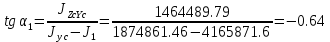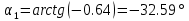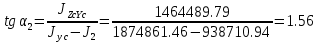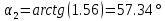











1.9 Откладываем главные оси 1,2 (рис 1,г)


г)

в)

70,1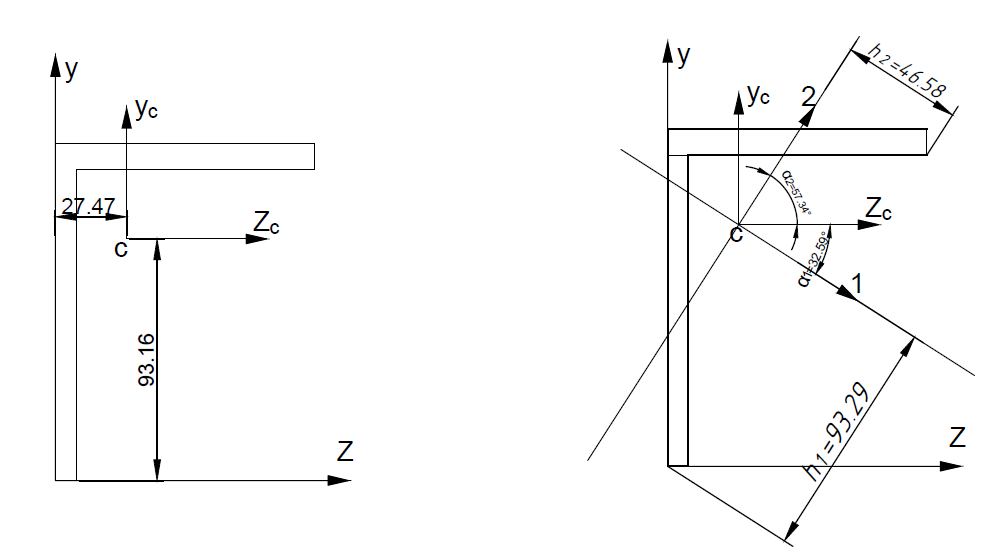


1.10 Определяем моменты сопротивлений относительно главных центральных осей 1,2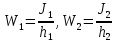



h₁, h₂ – расстояние от наиболее удаленных от главных осей точек поперечного сечения. Измеряем по чертежу (рис 1,г). Тогда: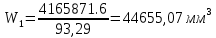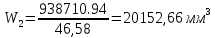




Пункт 2.

Дано: Р=30кН, а=1,7м, L=3м.

Определяем опорные реакции Ra и Rc: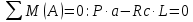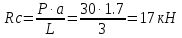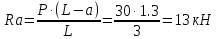










Рассматривая эпюру изгибающих моментов, можно определить, что опасным сечением балки является сечение, где приложена сосредоточенная сила P. Mmax=22.1кНм. Расчетная нагрузка при этом равна Qy=17кН.
Пункт 3

3.1 Проведем нейтральную ось через центр тяжести нашего профиля (нейтральная ось совпадает с осью Zc), тогда в качестве момента инерции всего сечения относительно его нейтральной оси Jz принимаем значение Jzc=3229721.08 мм⁴ .

3.2 Построение эпюры нормальных напряжений. Расчет значений в характерных точках 0,1,2,3,4: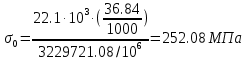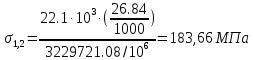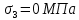







Нормальные напряжения профиля в сечении нейтральной оси равны нулю.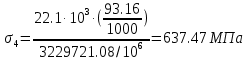


3.3 Построение эпюры касательных напряжений. Расчет значений в характерных точках 0,1,2,3,4: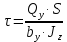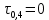



, так как выше точки 0 и ниже точки 4 площадь сечения равна нулю, поэтому касательных напряжений там нет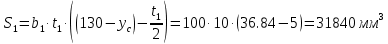



b_y1 = b₁=100мм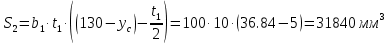





b_y2 = t₂= 8мм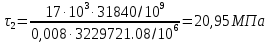





b_y3 = t₂= 8 мм




Рисунок 2 – Эпюры нормальных и касательных напряжений

3.4 Определение эквивалентных напряжений в характерных точках: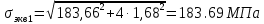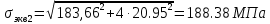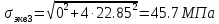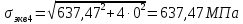












Наиболее опасной точкой в наиболее опасном сечении балки является точка 4
Пункт 5

По третьей гипотезе прочности:


По условию []=320МПа. Для 4 точки =0. Тогда:

_экв = []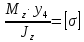



В данном выражении только величина Mz зависит от нагрузки Р. Для нашего случая обозначим Р=Ркр. Тогда: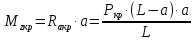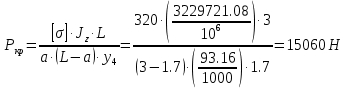






Пункт 4

Как выяснили в пункте 3, наиболее опасной точкой является точка 4. В этой точке касательные напряжения равны нулю. Из пункта 5 мы получили зависимость: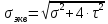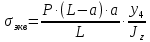





Подставляя численные значения в итоге получим:



График зависимости представлен на Рисунке 3.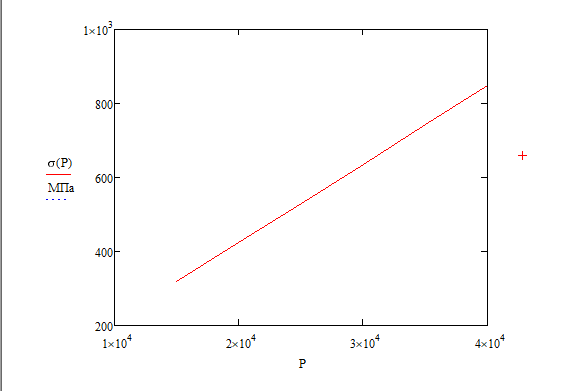



Рисунок 3 – График _экв=f(P)

Расчет профиля в программа Femap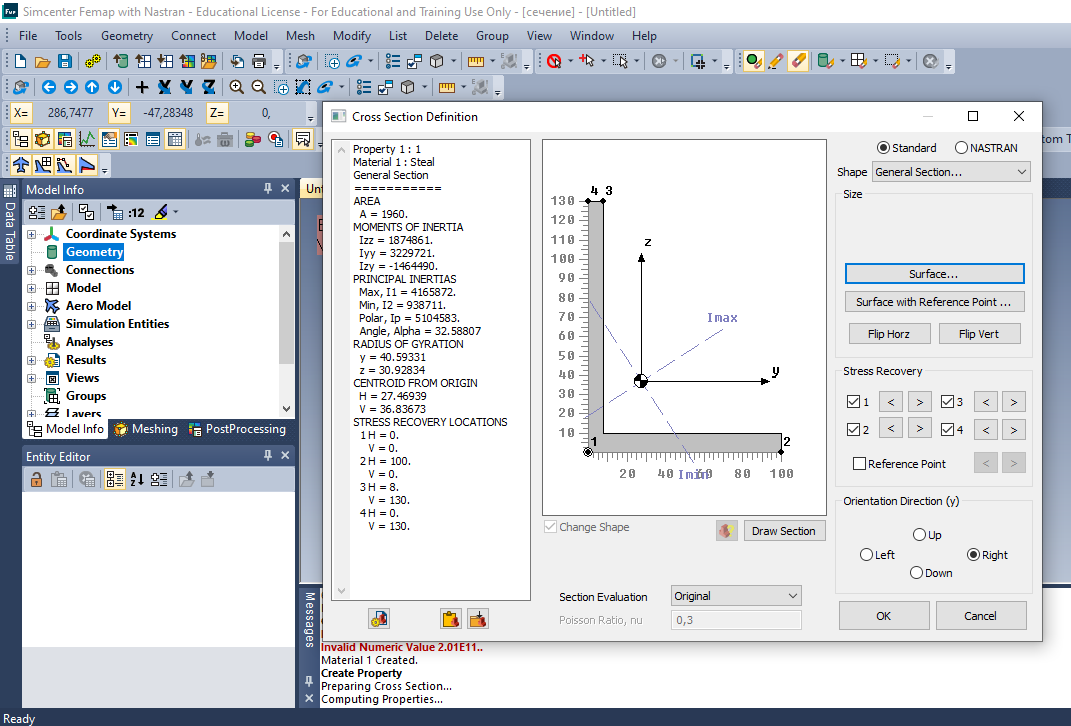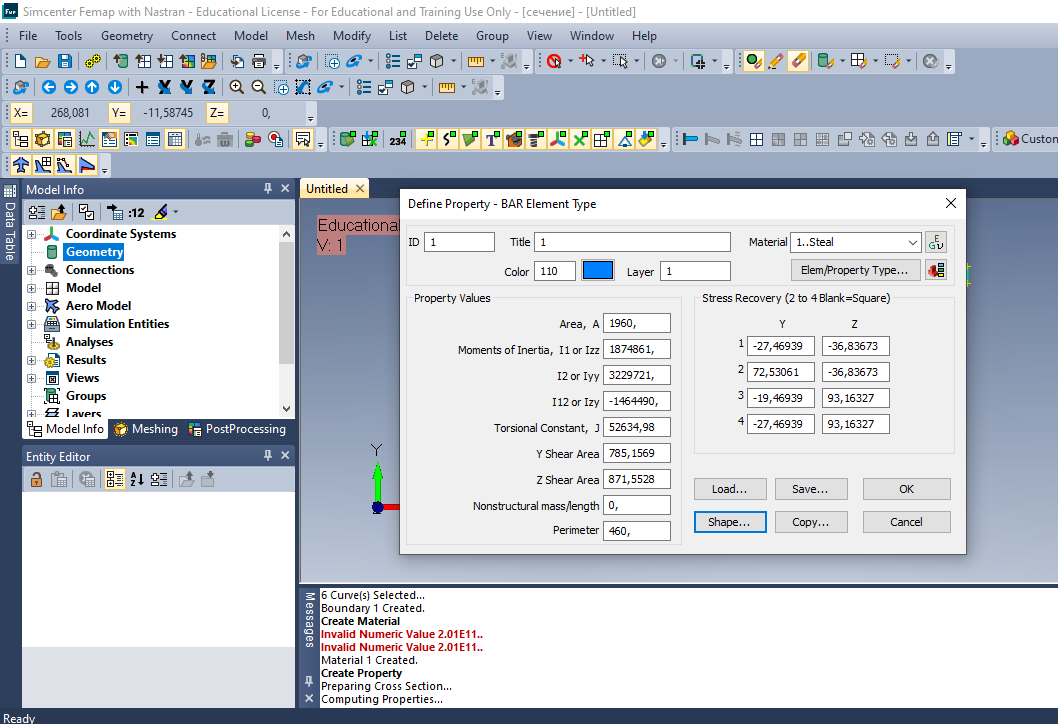