Задания. Решение. Радиус сходимости степенного ряда можно найти по формуле Т. к и, то
 Скачать 90.5 Kb.
|
|
Задание 4. Найти область сходимости ряда: 8)  .Решение. Радиус сходимости степенного ряда можно найти по формуле:  . Т.к.  и  , то .Итак, радиус сходимости ряда 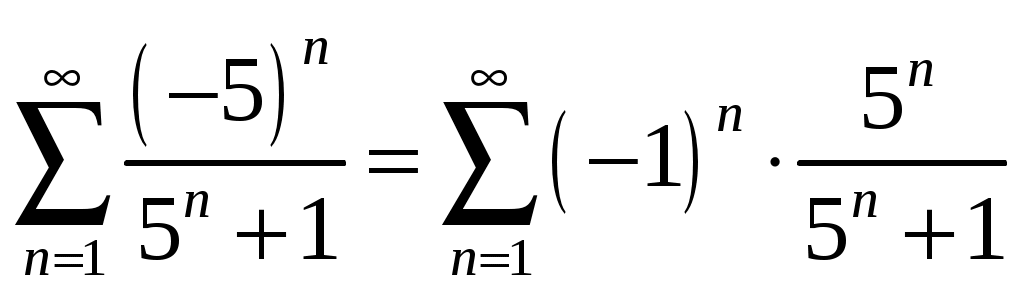 . Определим интервал сходимости данного степенного ряда: .Т.о.,  – интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.Пусть  . Подставим в заданный степенной ряд и получим знакочередующийся ряд .Для членов полученного ряда:  В соответствии с признаком Лейбница данный ряд расходится и не принадлежит области сходимости степенного ряда.Пусть  . Подставим в заданный степенной ряд и получим числовой ряд с положительными членами: .Получили расходящийся ряд, так как не выполняется необходимое условие сходимости 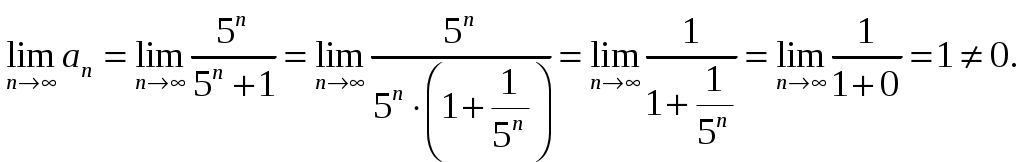 . Следовательно, ряд расходится и не принадлежит области сходимости степенного ряда. Итак, областью сходимости данного степенного ряда является промежуток .Ответ: .Задание 5. Вычислить с точностью до 0,001 интеграл, разлагая подынтегральную функцию в степенной ряд 8) 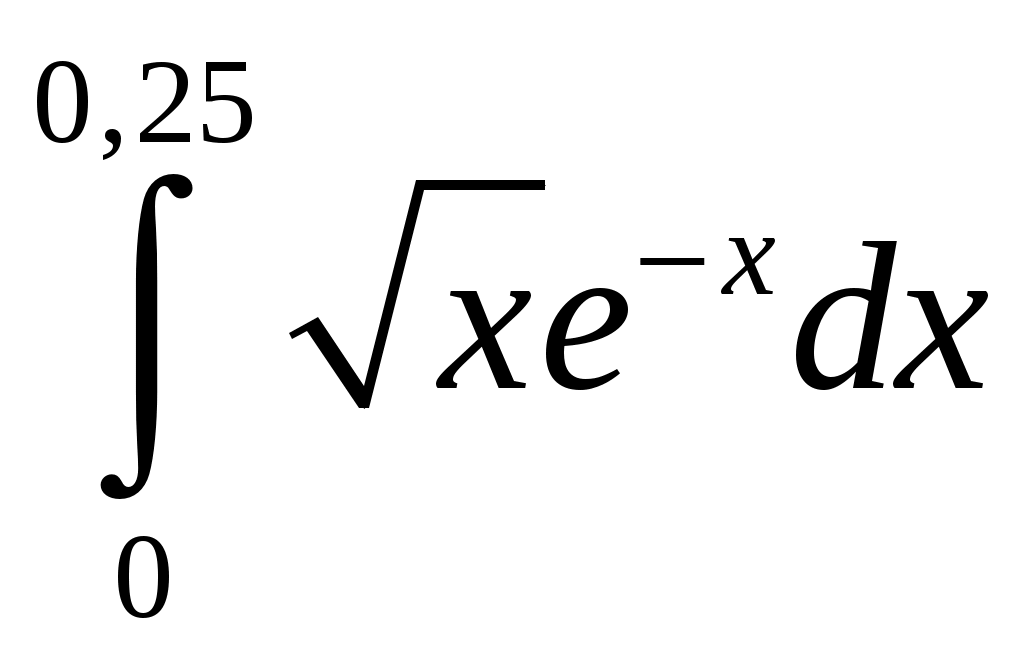 .Решение. Воспользуемся разложением подынтегральной функции в ряд. Используем формулу:  Получаем: 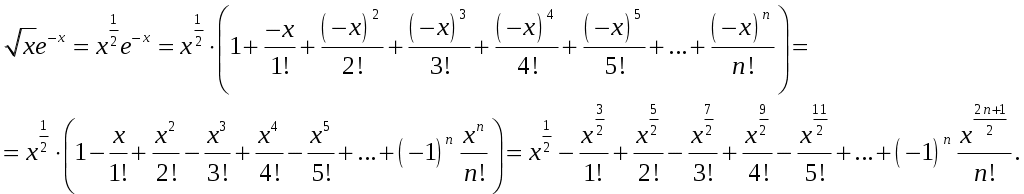 Тогда заданный интеграл: 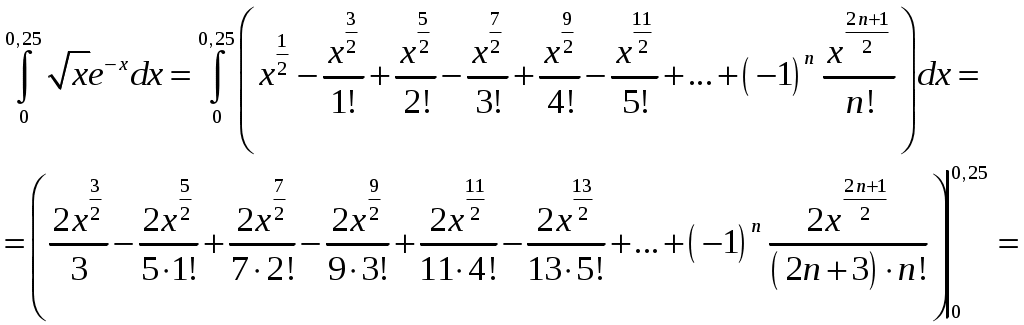 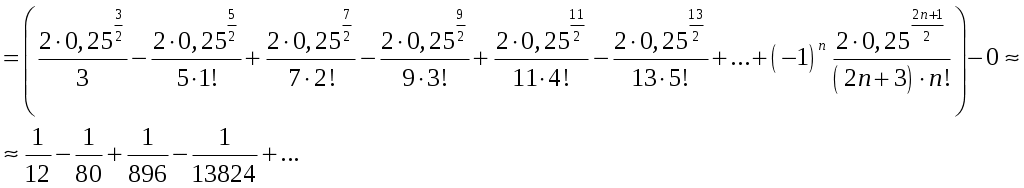 Погрешность замены суммы ряда суммой его первых n членов по абсолютной величине меньше первого из отброшенных членов.Т.к. четвертый член разложения 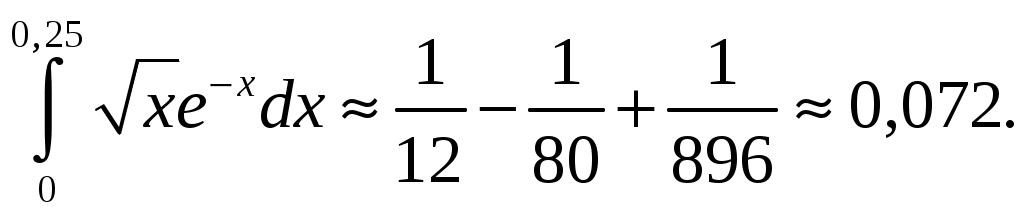 , то заданный интеграл будет: Ответ: 0,072. |