Линейная алгера и геометрия контрольная работа. кр лин 1 курс 1 семестр 5_variant. Решение Рассмотрим алгоритм метода Гаусса. Пусть дана система уравнений При решении методом Гаусса система приводится к ступенчатому виду

• Название: Решение Рассмотрим алгоритм метода Гаусса. Пусть дана система уравнений При решении методом Гаусса система приводится к ступенчатому виду
• Анкор: Линейная алгера и геометрия контрольная работа
• Дата: 30.03.2021
• Размер: 306 Kb.
• Имя файла: кр лин 1 курс 1 семестр 5_variant .doc
• Тип: Решение; #189468

Контрольная работа
Вариант 5
Задача 5

Используя метод Гаусса, найти решение системы или доказать её несовместность.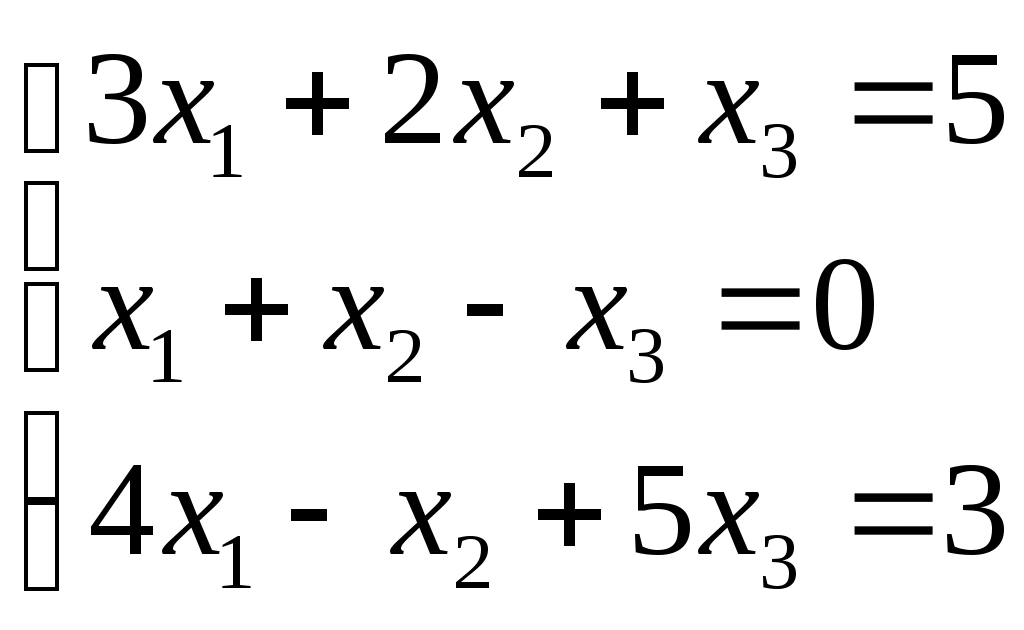


Решение

Рассмотрим алгоритм метода Гаусса. Пусть дана система уравнений: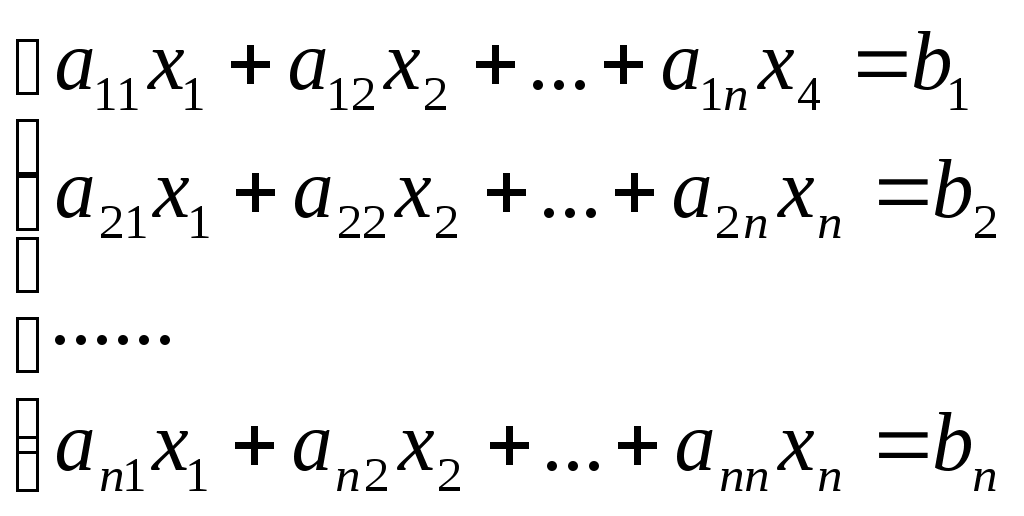



При решении методом Гаусса система приводится к ступенчатому виду: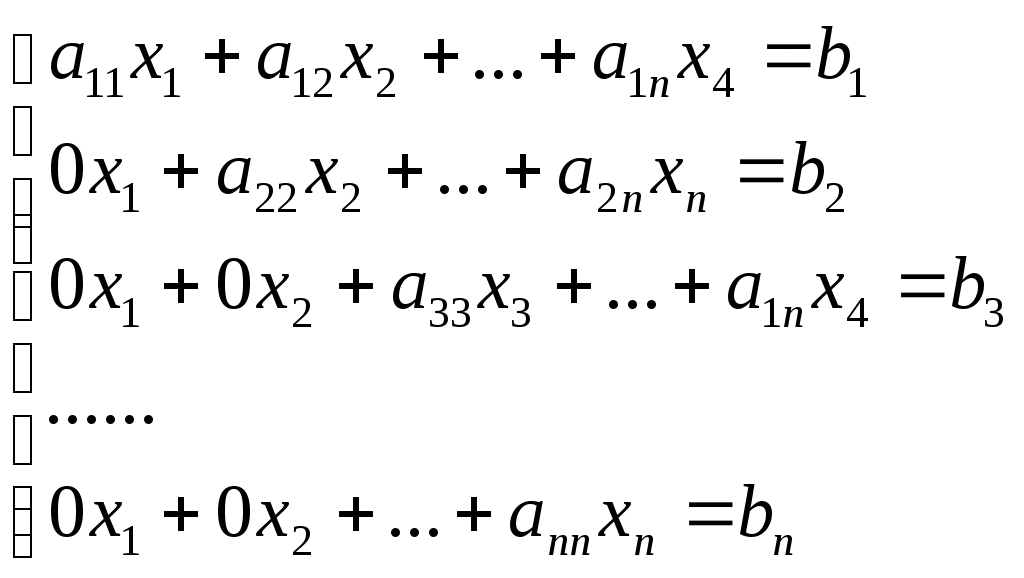



Для решения уравнения методом Гаусса необходимо знать, как выполняются элементарные преобразования систем линейных уравнений. Таких преобразований имеется четыре типа:

1. Умножение обеих частей уравнения на любое ненулевое число.

2. Перестановка уравнений системы местами.

3. Добавление (или вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженного на любое ненулевое число.

4. Удаление нулевых строк.

Общие зависимости прямого хода для расширенной матрицы:

Ведущее уравнение не изменяется.

Для последующих уравнений , i = k + 1,…, n; j = k + 1,..., n.

Обратный ход начинается с вычисления последнего неизвестного системы линейных уравнений и заканчивается вычислением первого неизвестного. При обратном ходе используются только строки прямого хода.

Формулы обратного хода для полученной матрицы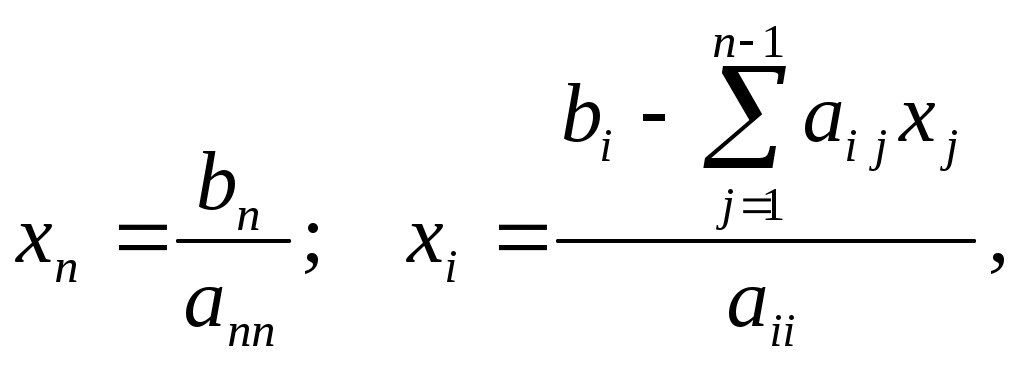

i = n – 1,…,1

Запишем расширенную матрицу системы: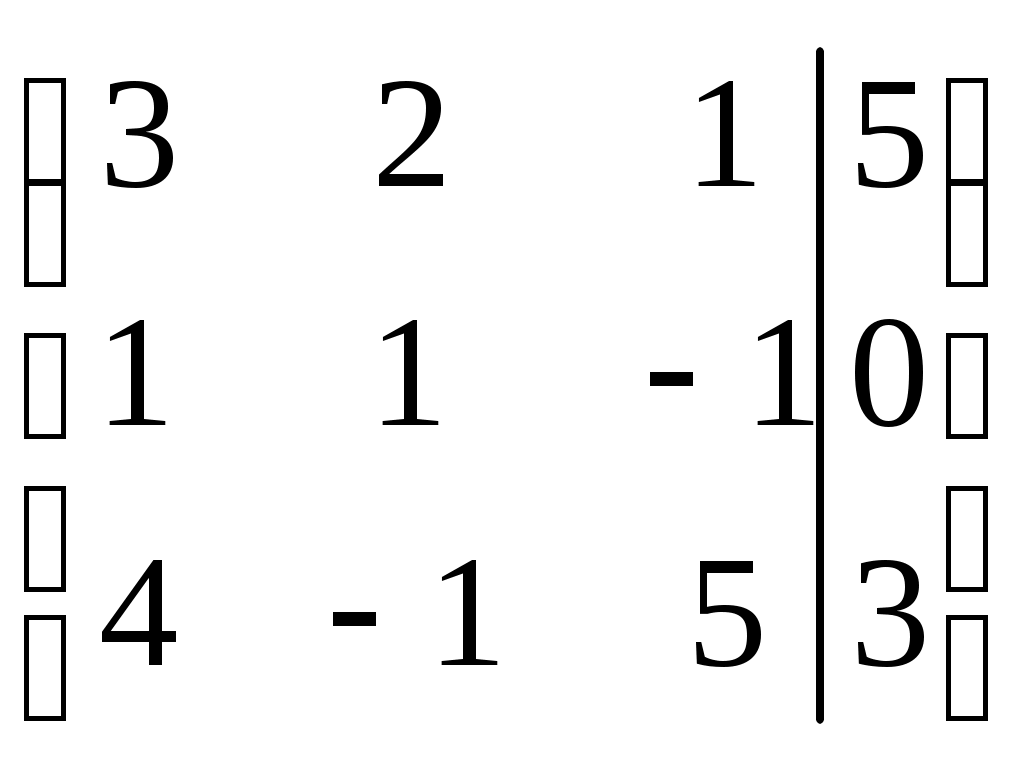



На первом шаге с помощью первого уравнения х₁ исключаем из других уравнений. Для этого:

• 
  Вычитаем из второй строки, умноженной на 3 первую, и записываем вместо второй строки
  
• 
  вычитаем из третьей строки, умноженной на 3, умноженную на 4 первую и записываем вместо второй строки. Первую строку оставляем без изменения
  

Получим: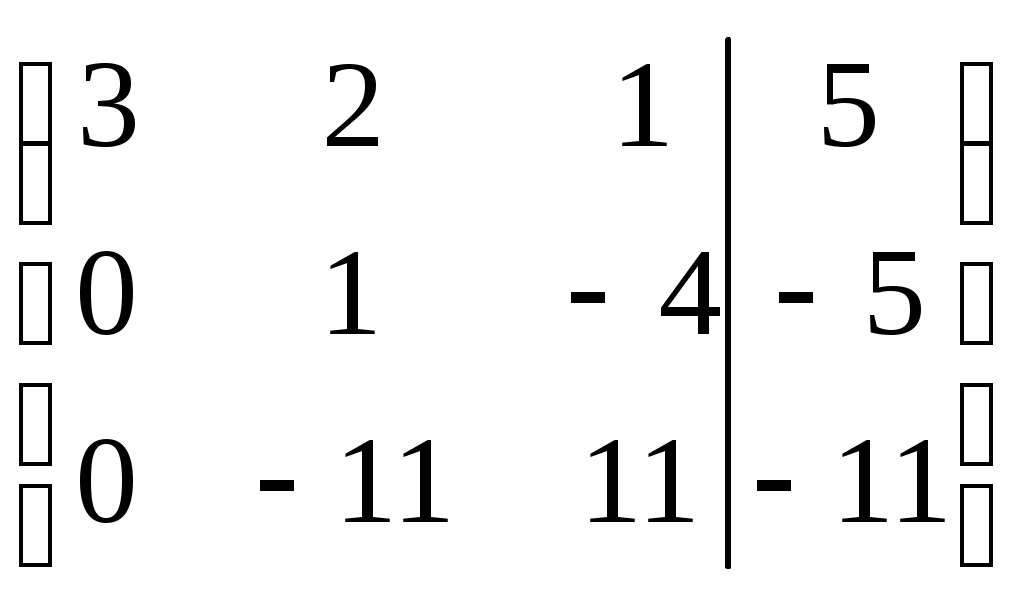



Разделим третью строку на 11. Получим: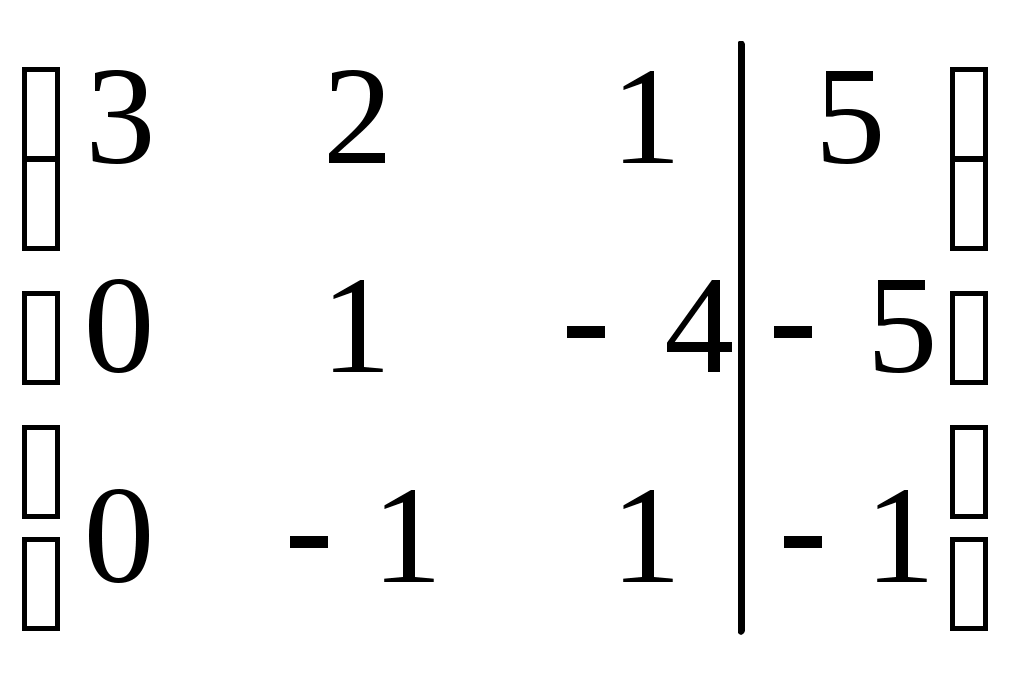



Исключаем х₂ из третьего уравнения, для этого к третьей строке прибавляем вторую и записываем на место третьей. Остальные строки не изменяем. Получим: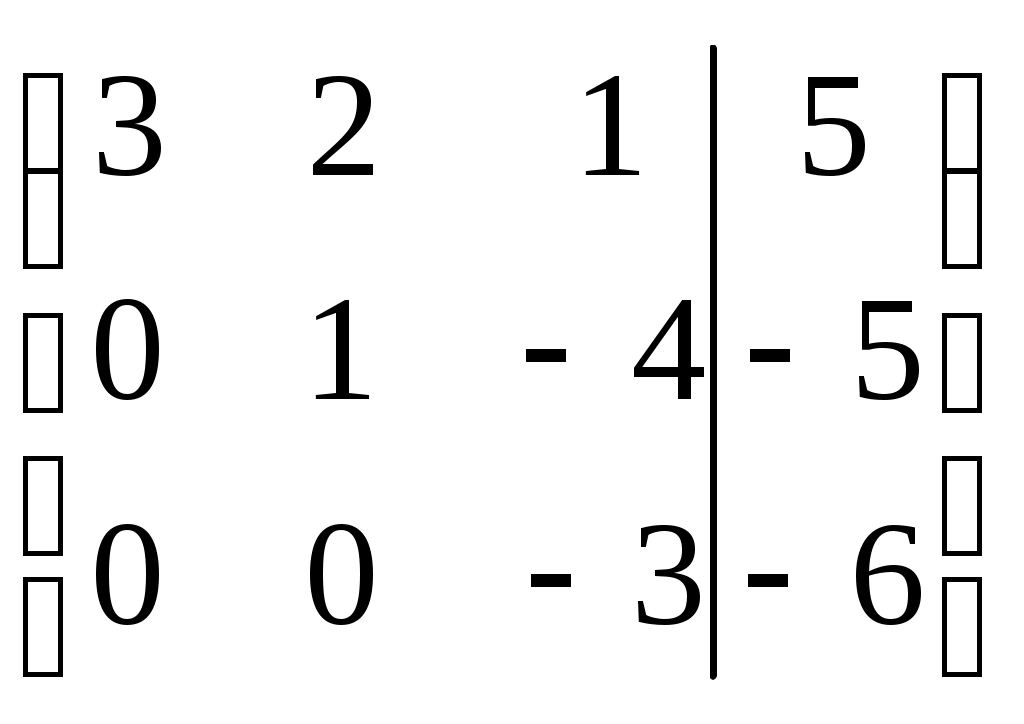



Матрица приведена к ступенчатому виду. Выполняем обратный ход.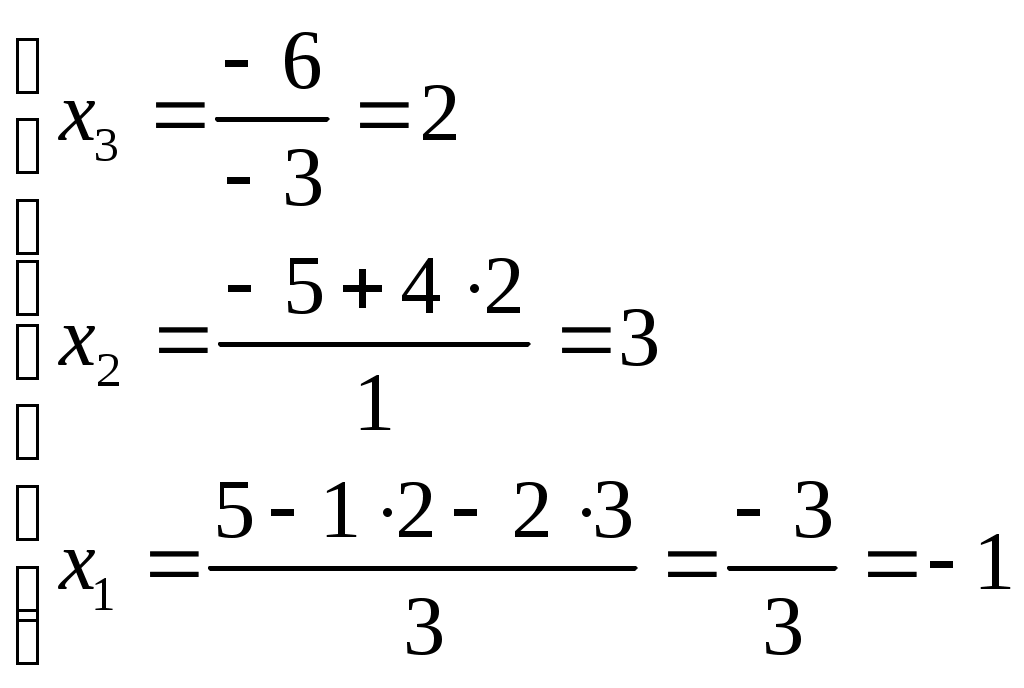



Получено решение: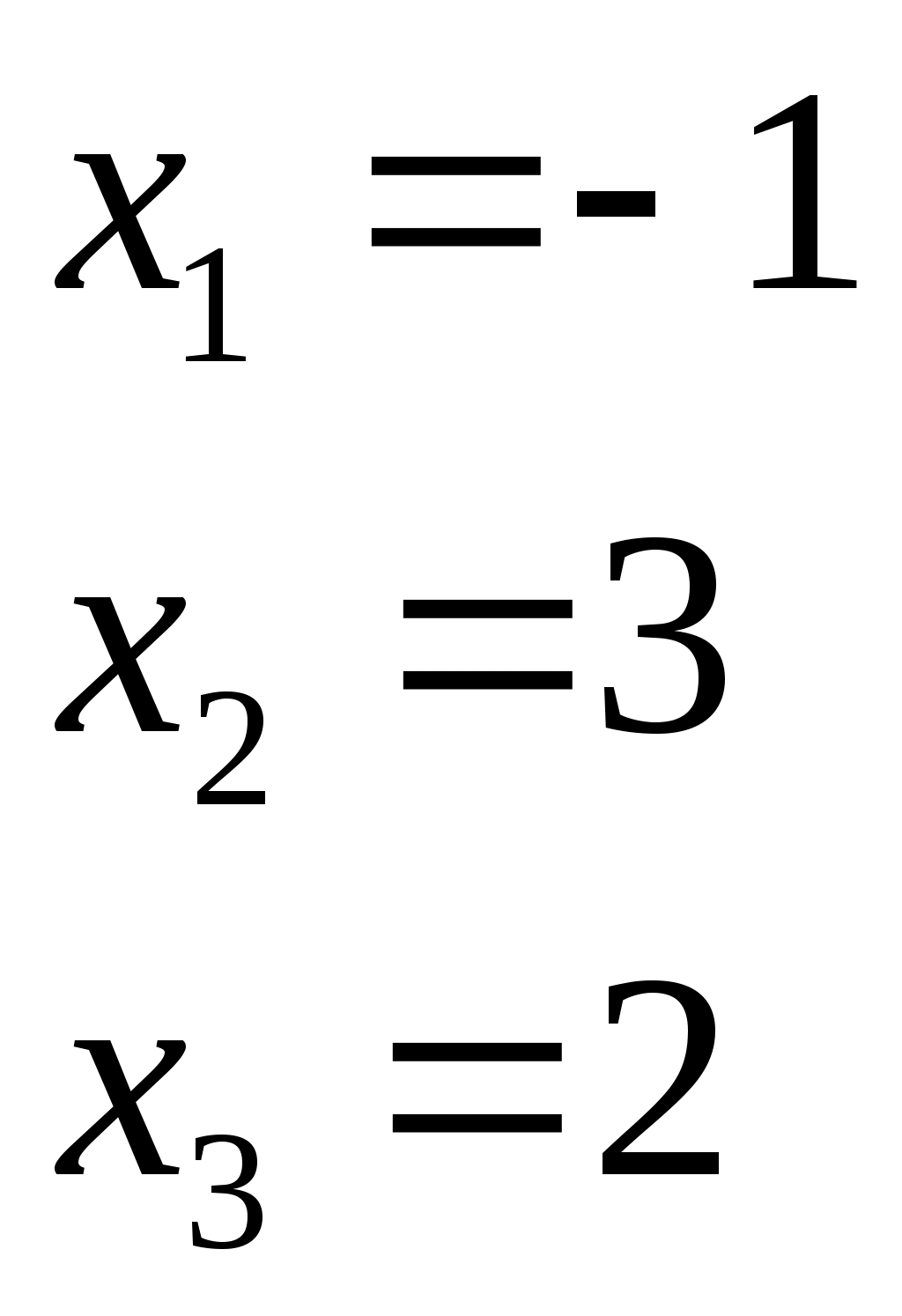



Ответ:_Задача_15'>Ответ: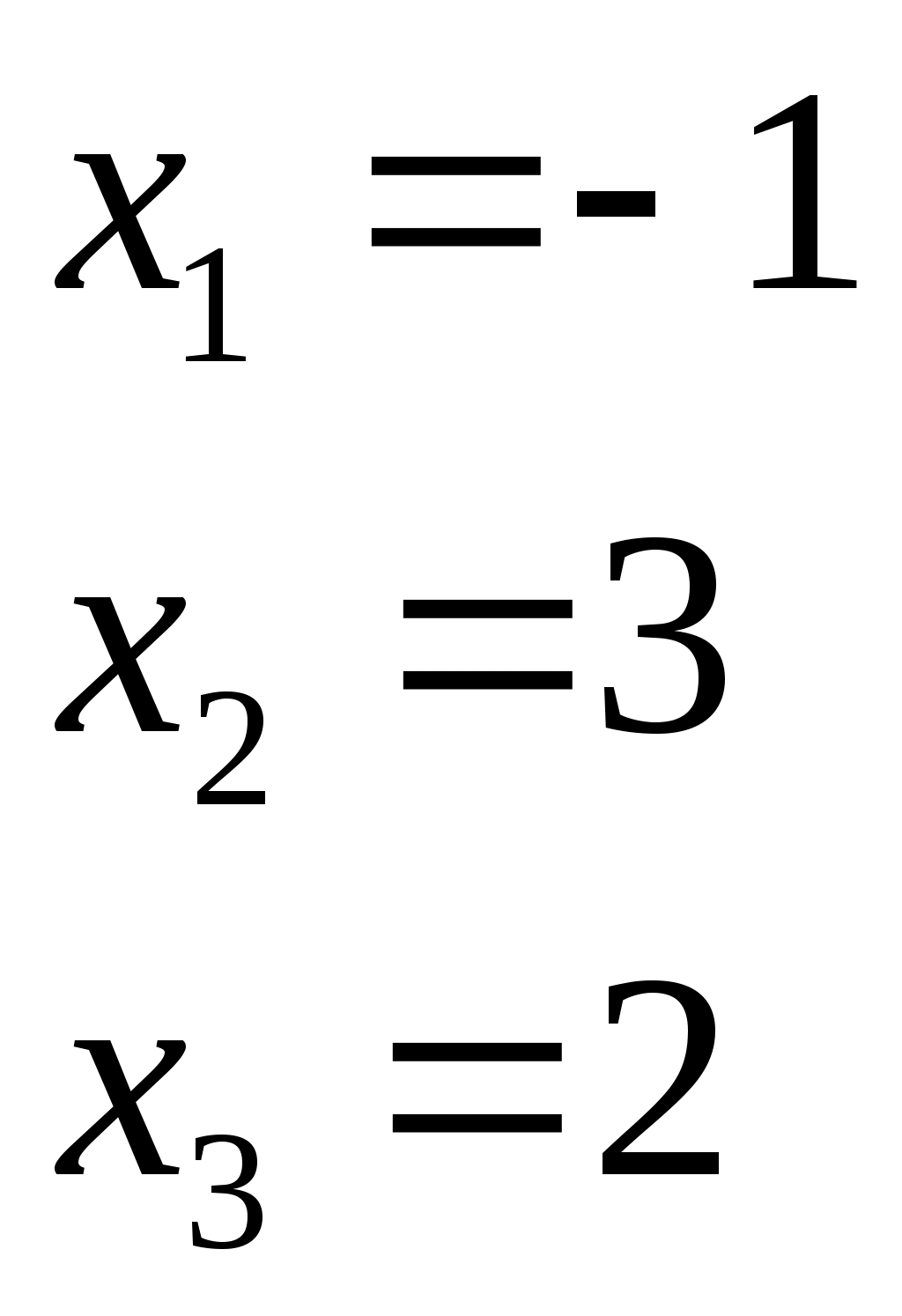



Задача 15

Дана матрица А.

1) Найти обратную матрицу А^-1 и проверить, что А^-1А=АА^-1= Е.

2) При помощи обратной матрицы найти решение x₁, x₂, x₃ системы, записанной в матричной форме AX=B, где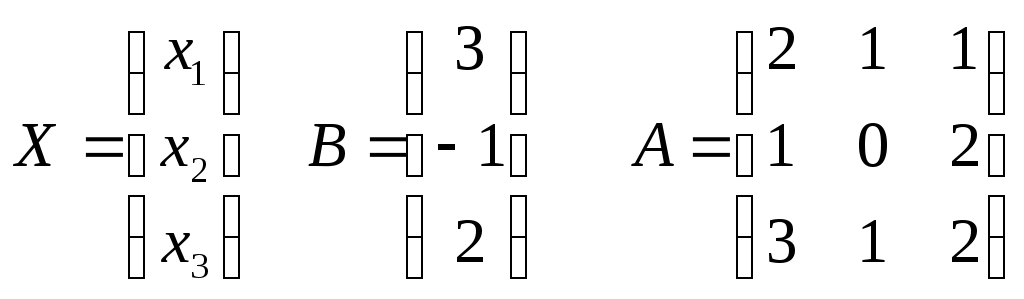

Решение

1) Найдем обратную матрицу А^-1.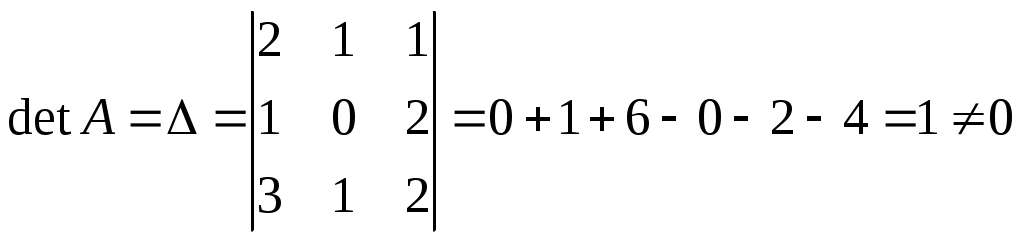



Определитель не равен 0, обратная матрица существует.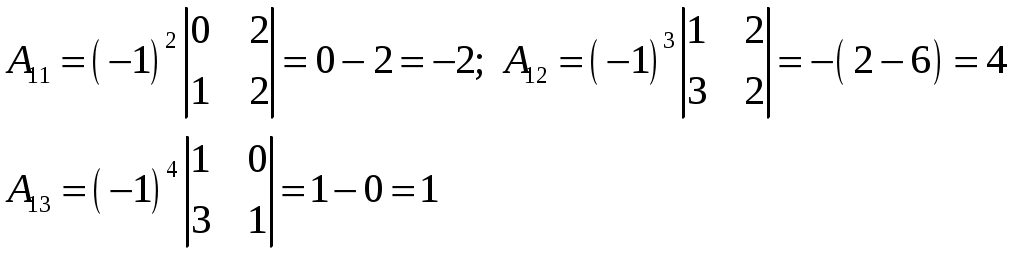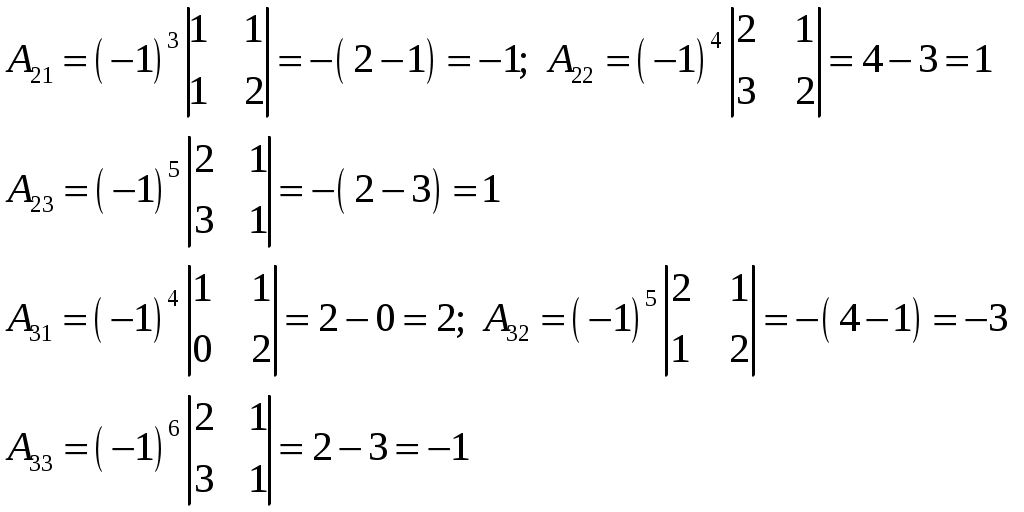





Отсюда: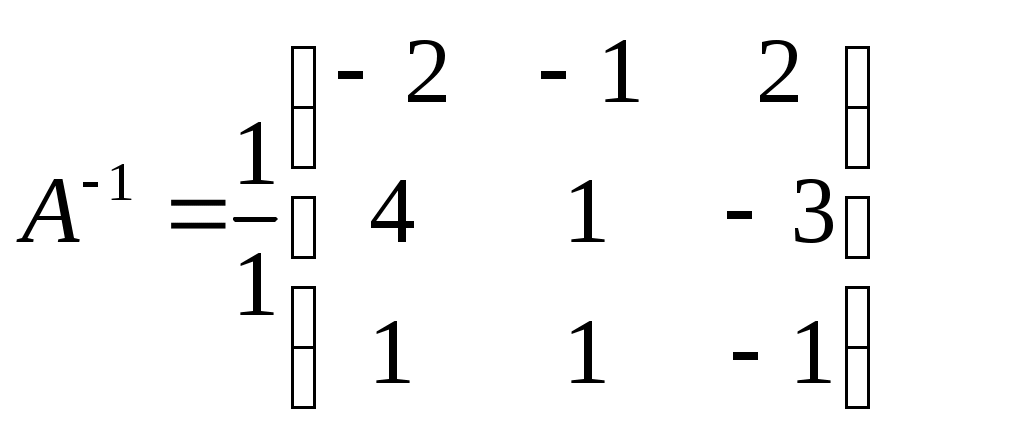

Проверим равенство АА^-1 = Е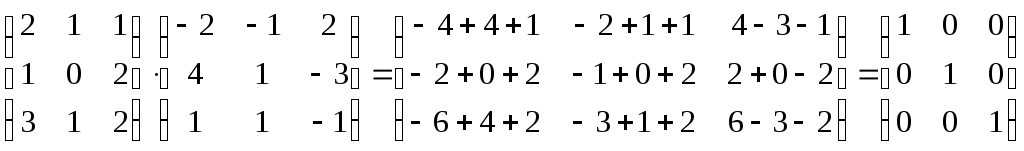



Равенство выполнено.
Проверим равенство А^-1А = Е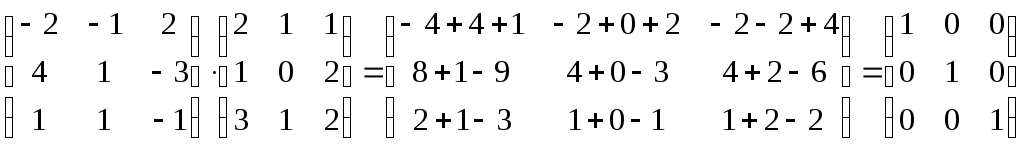



Равенство выполнено.

2) Найдем решение матричного уравнения АХ = В.

В данном случае Х = А^-1В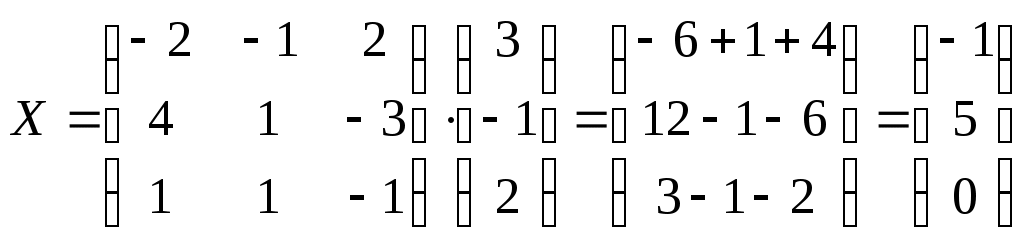



Ответ:

1)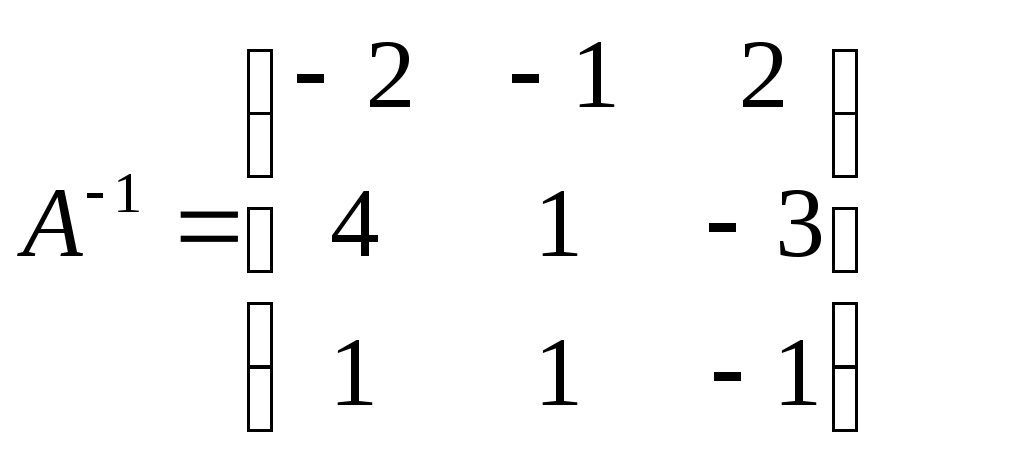
2)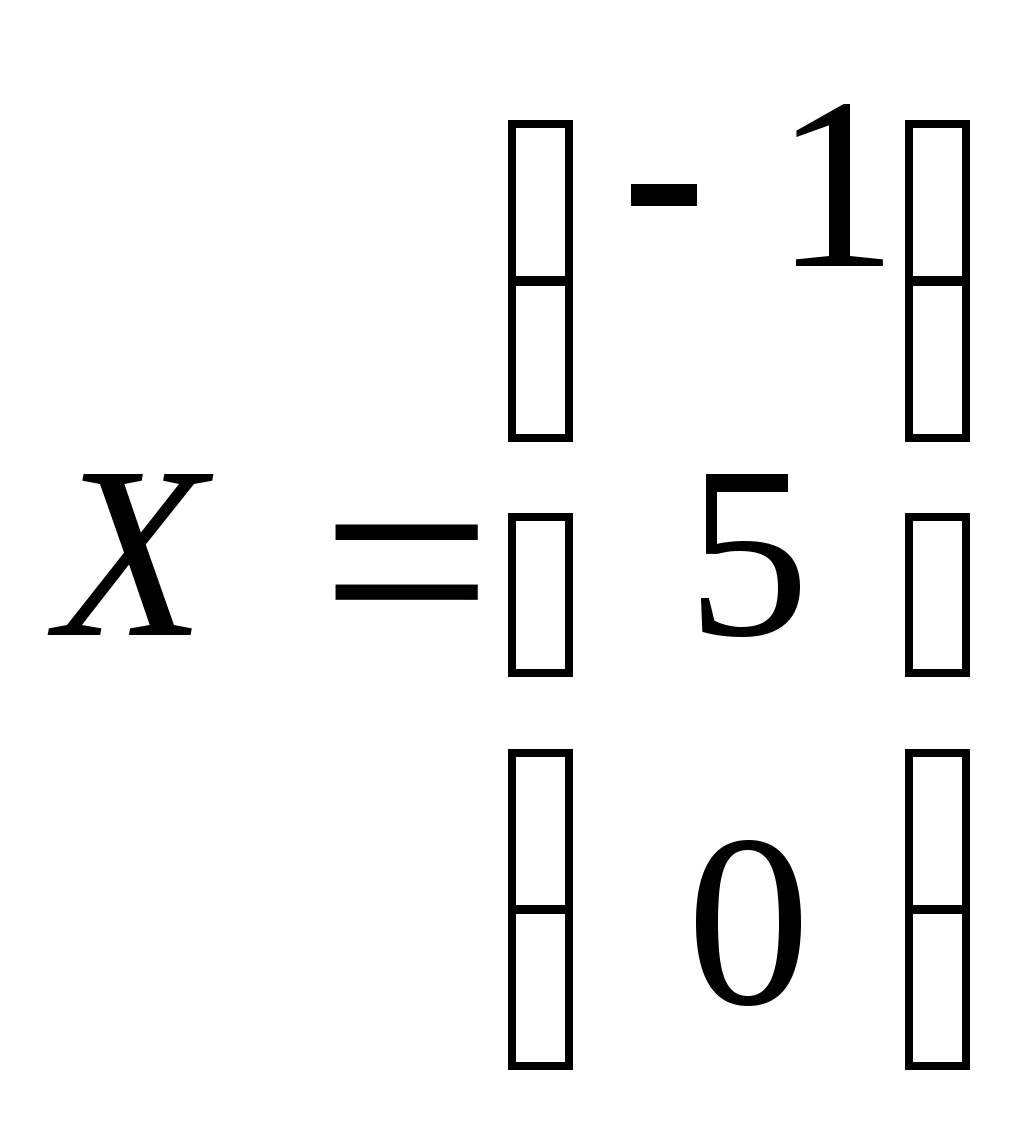
Задача 25

Найти x₁ по формулам Крамера.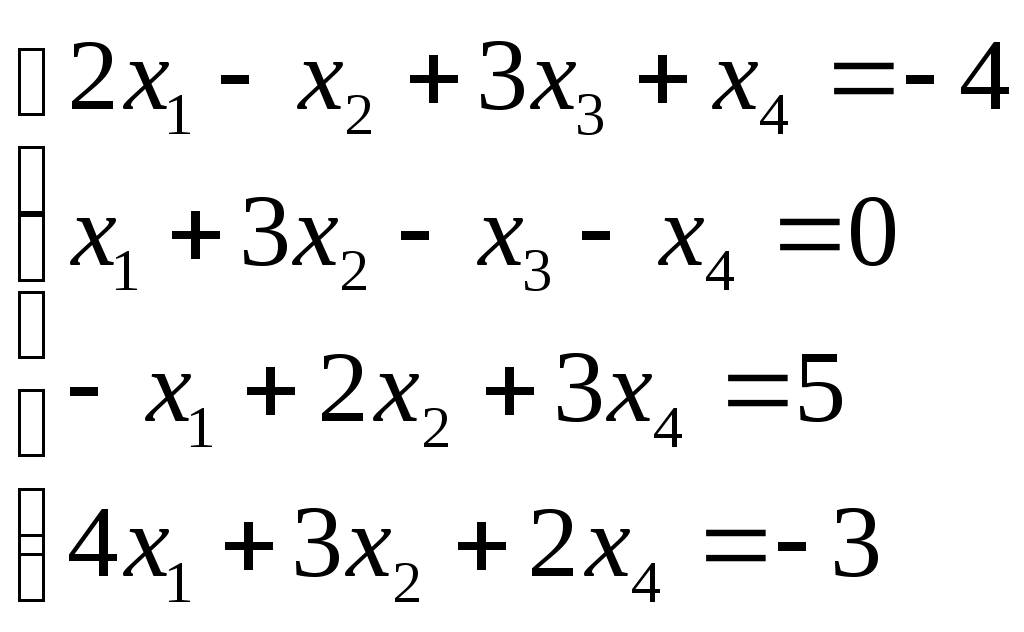


Решение

Формулы Крамера:

В данном случае

Найдем определитель: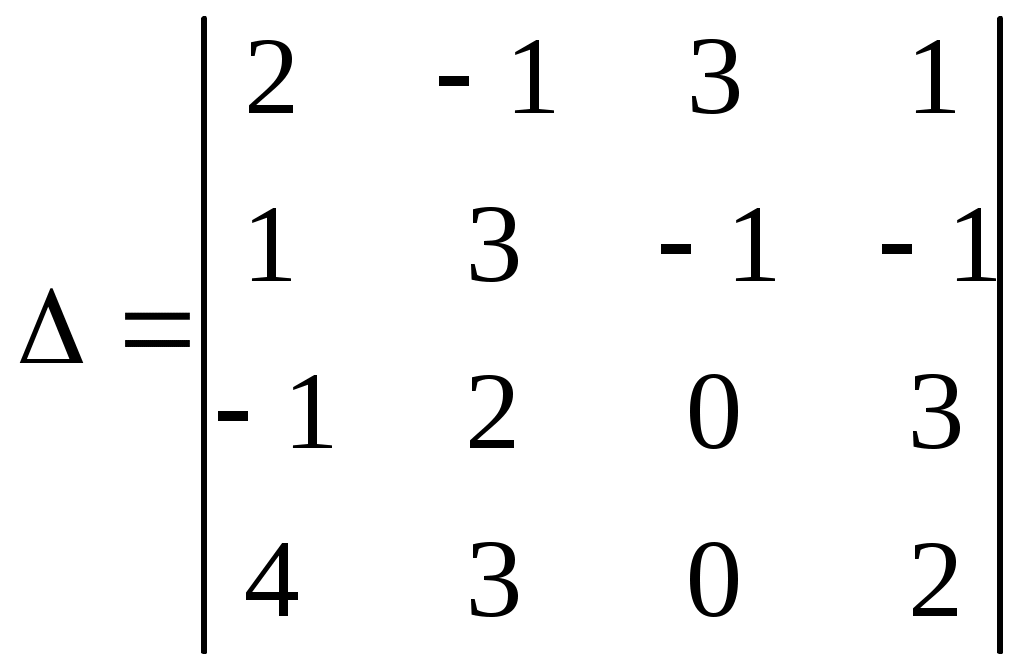

В данном случае будем использовать общую формулу разложение определителя по столбцу:  Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:
В третьем строке имеем два нулевых элемента, будет использовать формулу для нахождения определителя по третьему столбцу: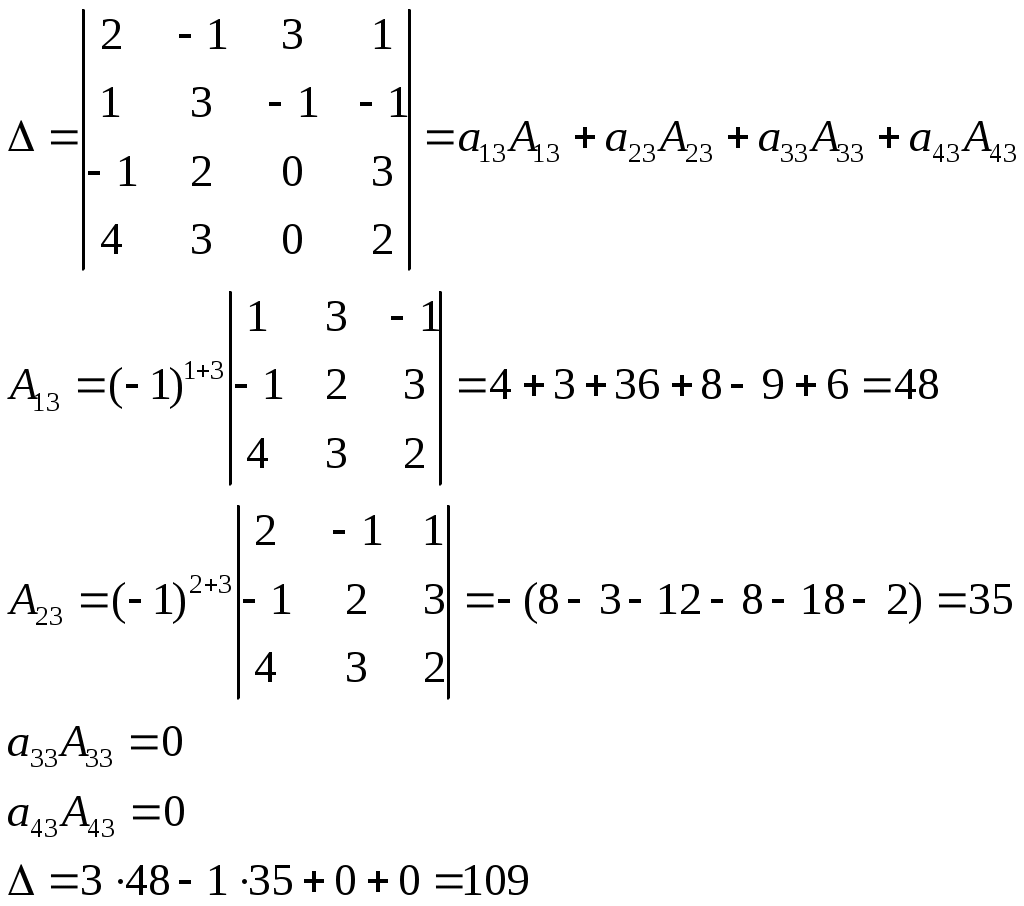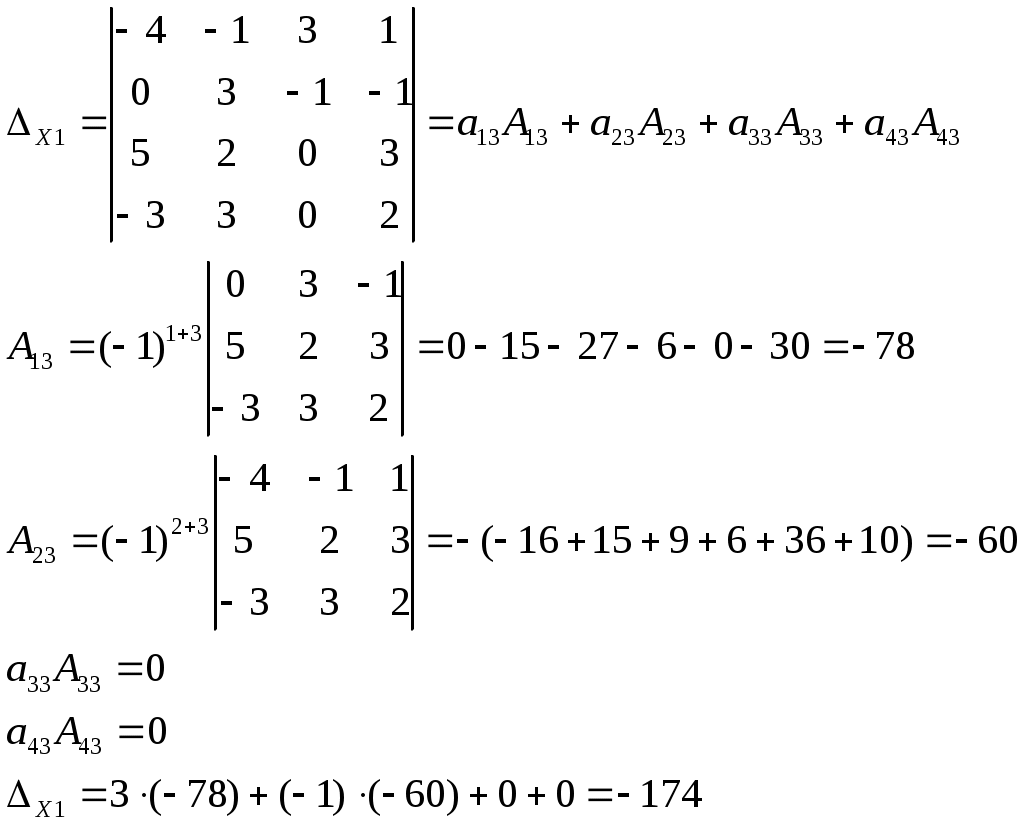





Отсюда по формулам Крамера:
Ответ:


Задача 35

Найти:

1)

2) Площадь треугольника со сторонами, совпадающими с векторами и

3) Смешанное произведение векторов

4) λ при котором векторы и ортогональны.


Решение

1) Формула для проекции вектора на вектор

Найдем координаты вектора



Проекцию вектора найдем по данной формуле:


2) Найдем площадь треугольника со сторонами, совпадающими с векторами и

3) Смешанное произведение векторов .

Координаты вектора

Векторное произведение численно равно площади параллелограмма, построенного на данных векторах.

Следовательно, площадь треугольника, построенного на векторах равна половине векторного произведения. Отсюда: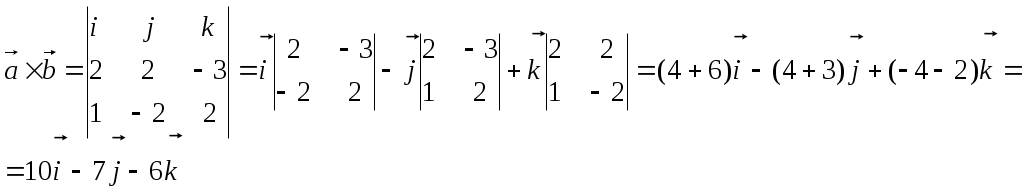



Тогда площадь треугольника:


3) Найдем смешанное произведение векторов .

Смешанное произведение векторов: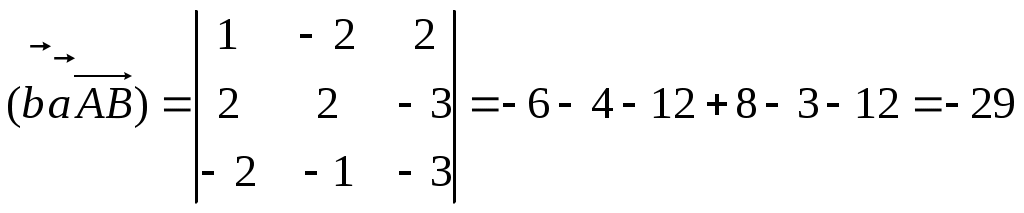


4) Вектора ортогональны, если их скалярное произведение равно 0. Для нахождения искомого числа найдем скалярное произведение векторов.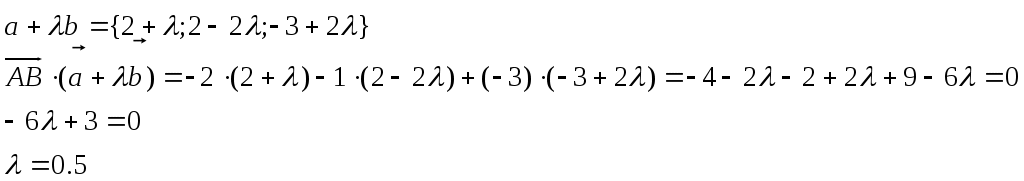




Ответ:

1)

2)

3)

4)


Задача 45

Найти:

1)

2) Длину вектора

Решение

1) Найдем скалярное произведение векторов: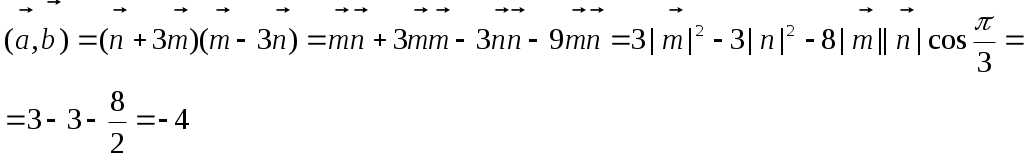



2) При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть  и  – векторы, α – угол между ними, а – сумма векторов как результат сложения векторов по правилу треугольника. Тогда верно следующее соотношение:



Где α’ – угол, смежный с углом α.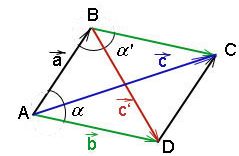


В этом случае длина разности тех же векторов:



Отсюда модуль вектора :



Модуль вектора :



Так как скалярное произведение равно: , то:



Так как , то



Модуль векторного произведения:


Ответ:

1)

2)

Задача 55

Найти:

1) уравнение прямой, проходящей через точки А и В;

2) уравнение прямой, проходящей через точку А перпендикулярно плоскости Р;

3) уравнение плоскости, проходящей через точку А, перпендикулярно прямой L.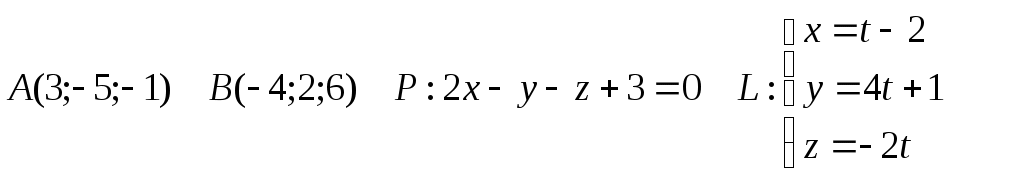

Решение

1) Если прямая проходит через точки (х₀, у₀, z₀) и (х₁, у₁, z₁), то ее уравнение:



Отсюда уравнение прямой АВ:

То есть:
2) Если прямая перпендикулярна плоскости, то нормальный вектор плоскости будет направляющим вектором прямой.

Если прямая проходит через точку (x₀; y₀; z₀) параллельно вектору , ее уравнение:

То есть, уравнение искомой прямой:
3) Если плоскость проходит через точку (x₀; y₀; z₀) перпендикулярно вектору , ее уравнение:

Если плоскость перпендикулярна прямой, то ее направляющий вектор будет нормальным вектором плоскости. Найдем каноническое уравнение прямой L.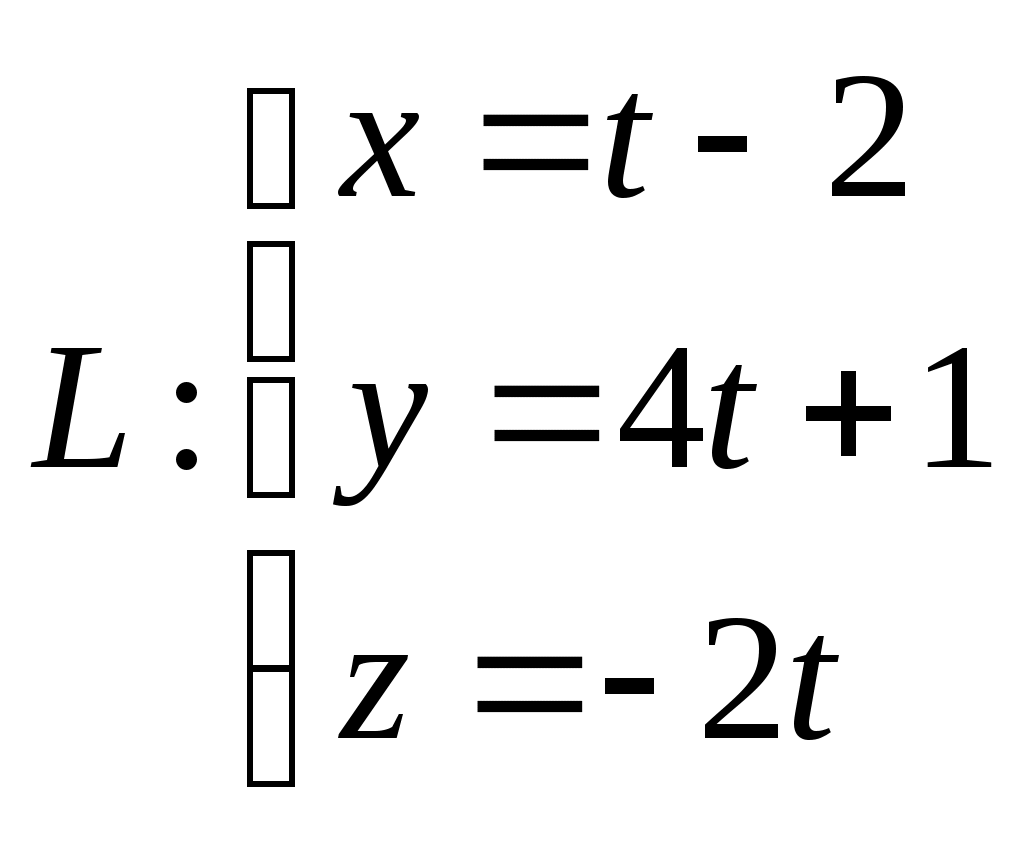



Отсюда:



Уравнение искомой плоскости:


Ответ:

1) Уравнение прямой, проходящей через точки А и В:

2) Уравнение прямой, проходящей через точку А перпендикулярно плоскости Р:



3) Уравнение плоскости, проходящей через точку А, перпендикулярно прямой L




Задача 65

Найти, при каких действительных x и y справедливо равенство, если z = x + iy .


Решение

Найдем значения отдельных выражений в левой части:



Найдем значение i²⁷

Для возведения в степень используем формулу Муавра для комплексных чисел, представленных в тригонометрической форме:



Так как:

𝑧 = 𝑖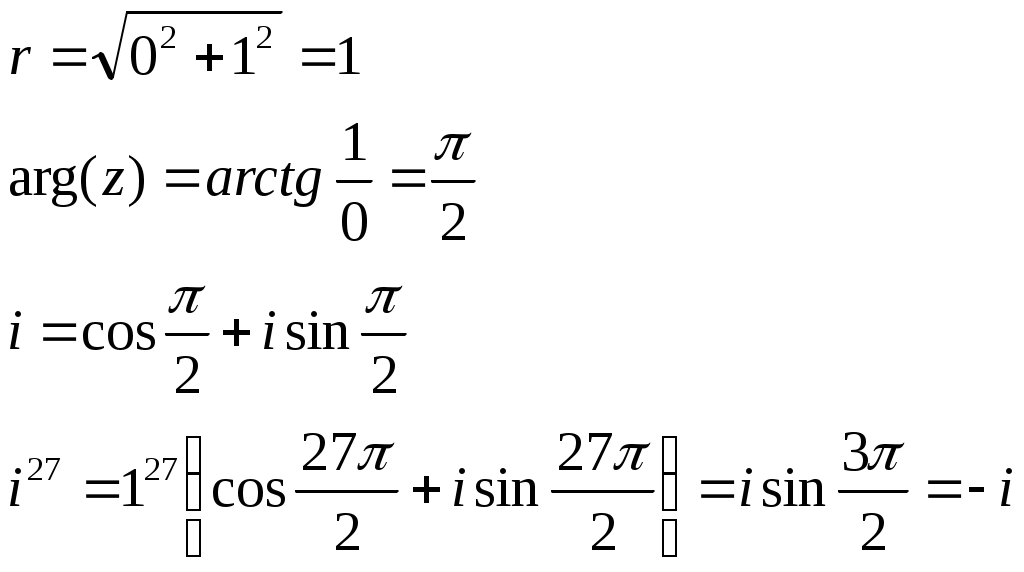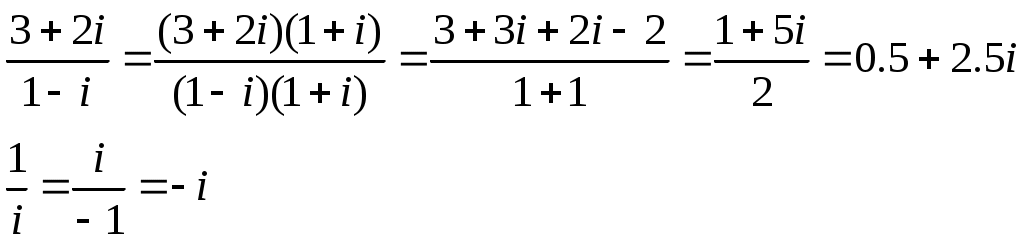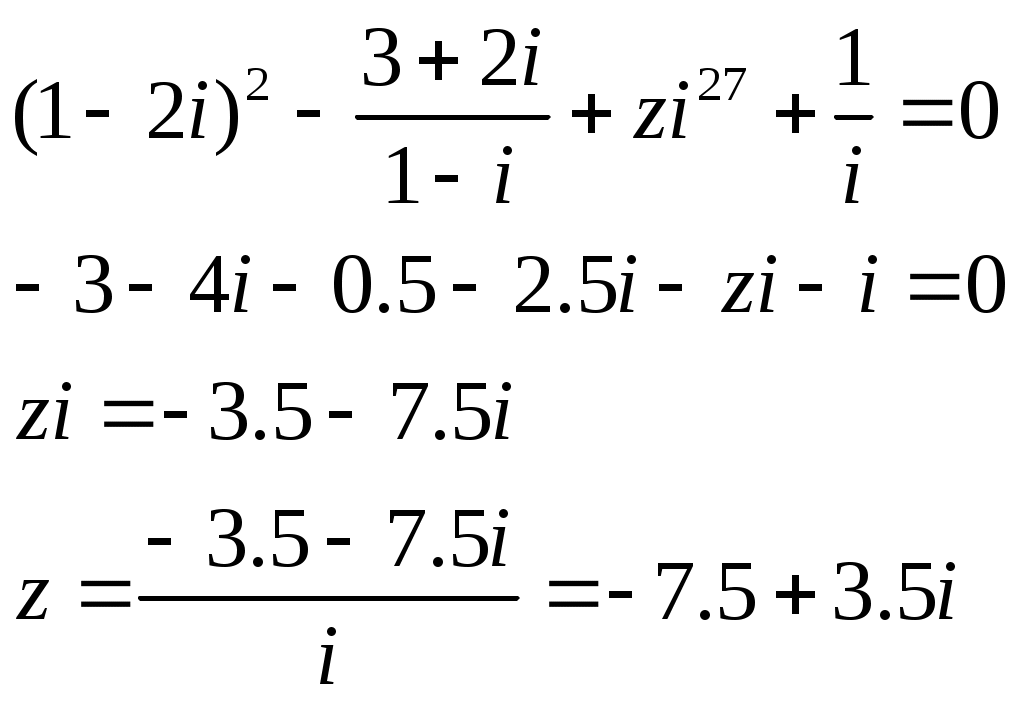






Ответ:

Задача 75

А) записать комплексное число z в показательной форме;

б) Вычислить и ответ записать в алгебраической форме


Решение

1) Для представления числа в показательной форме используем формулу: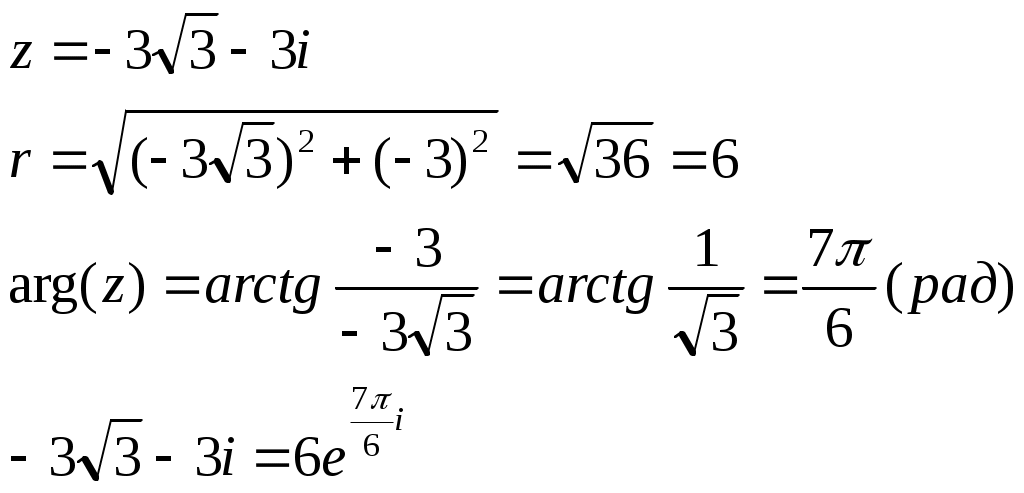





Угол получен, исходя из расположения числа (4 четверть).
2) Подставляем из условия: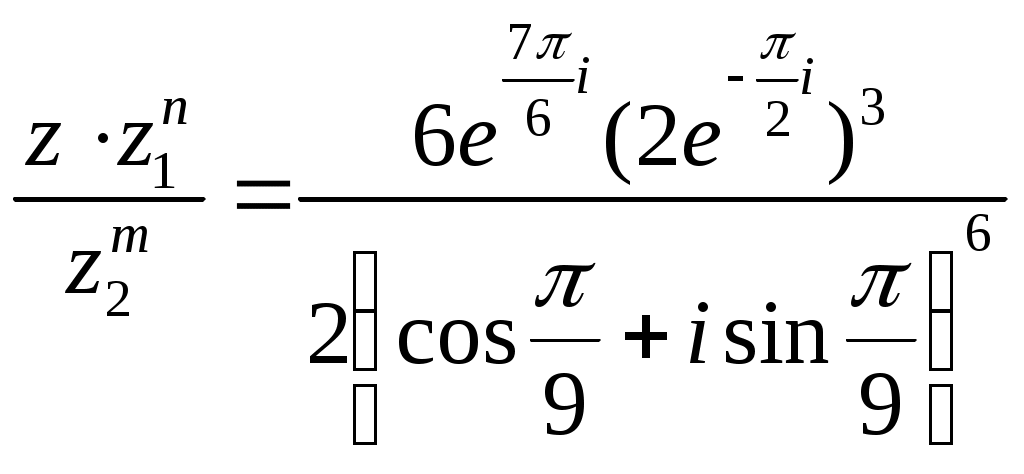



Находим значение выражений в числителе и знаменателе и переводи результат в алгебраическую форму: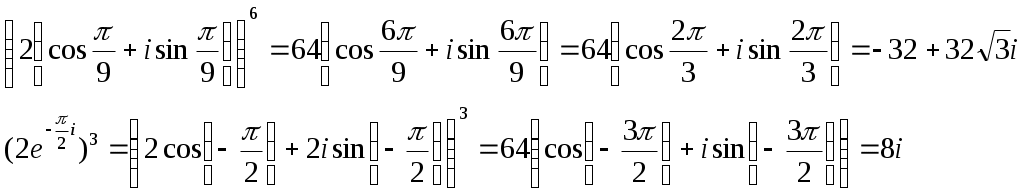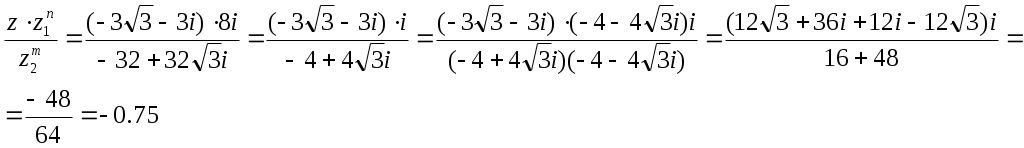




Ответ:

1)

2)