Решение Решим однородное уравнение, Для решения неоднородного уравнения, положим Подставим в уравнение

• Название: Решение Решим однородное уравнение, Для решения неоднородного уравнения, положим Подставим в уравнение
• Дата: 10.02.2018
• Размер: 172 Kb.
• Имя файла: 856270RE.doc
• Тип: Решение; #36190

Вариант №6 Этап №5

Задание 1. Решить задачу Коши для ДУ аналитически.

Задание 2. Решить задачу Коши численно методом Эйлера на . Число разбиений отрезка .

Задание 3. Построить график аналитического решения и все ломаные Эйлера на одном чертеже.



Решение: Решим однородное уравнение ,

Для решения неоднородного уравнения, положим

Подставим в уравнение



Общее решение неоднородного уравнения



Для определения положим ,

Точное решение

Метод Эйлера.

Разделим отрезок на равных частей точками

Полагаем .

Заменим производную разностным аналогом

.

Из дифференциального уравнения

Решение в Excel.

i	x	y
0	0	0
1	0.5	0
2	1	-0.16667

i	x	y
0	0	0
1	0.25	0
2	0.5	-0.08333
3	0.75	-0.33333
4	1	-0.91667

i	x	y
0	0	0
1	0.2	0
2	0.4	-0.06667
3	0.6	-0.26667
4	0.8	-0.73333
5	1	-1.73333

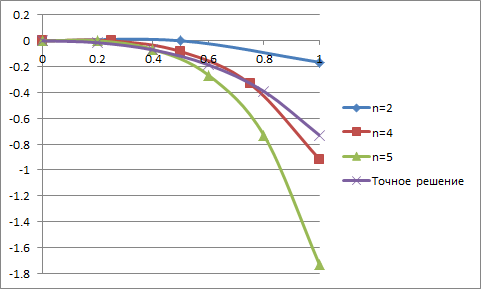Вариант №6 Этап №6

Задание 1. Решить задачу Коши для ЛОСУ методом Эйлера.

Задание 2. Исследовать систему на устойчивость. Построить траектории движения вблизи точки покоя.



Решение: Продифференцируем второе уравнение

,

Из системы



Подставляя в получим .

Из второго уравнения

Получим задачу Коши:



Характеристическое уравнение

Общее решение: .



Из начальных условий получим систему: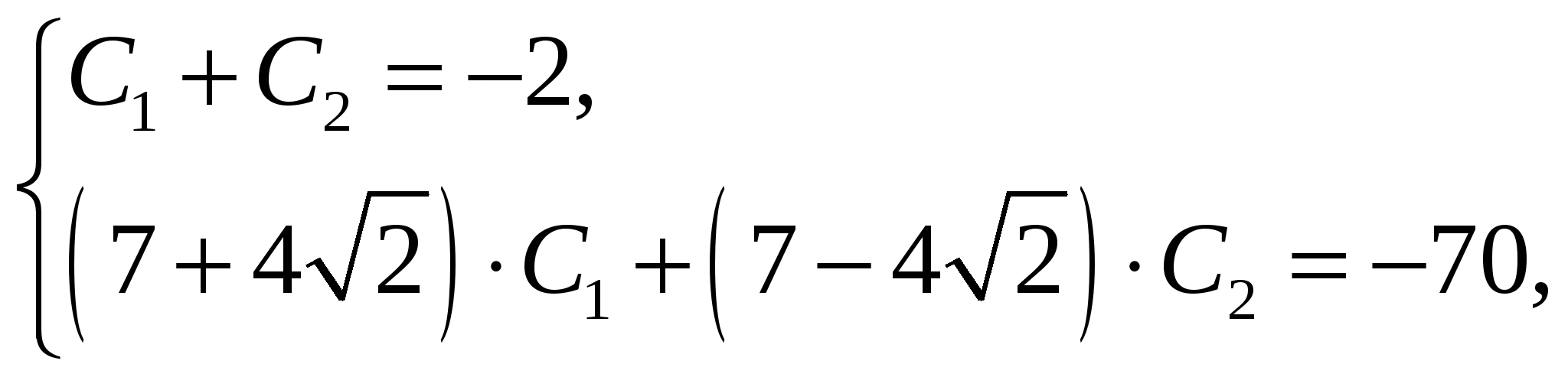



Решая систему и из соотношения .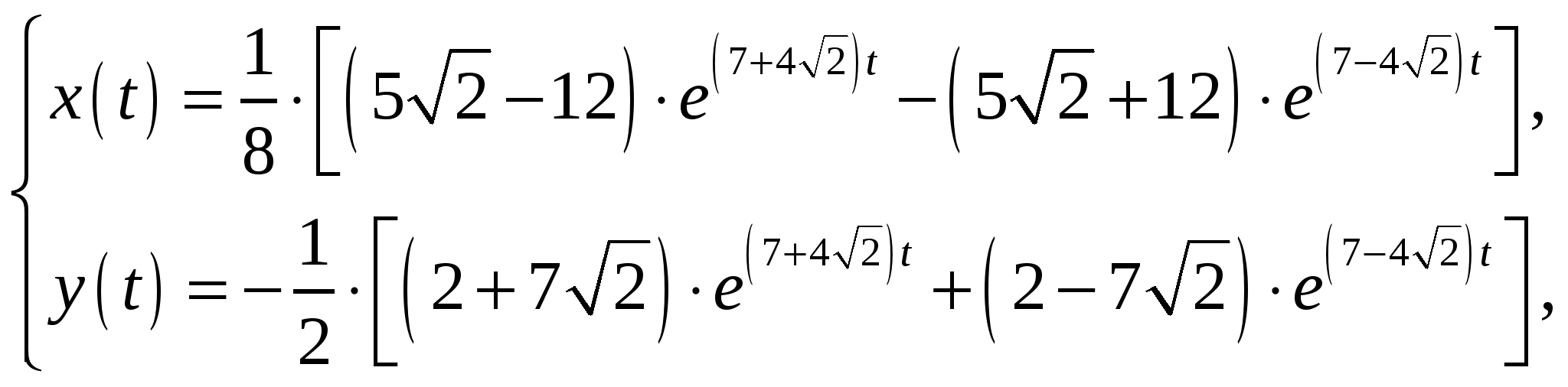



Метод Эйлера.

Положим .

Формулы расчета: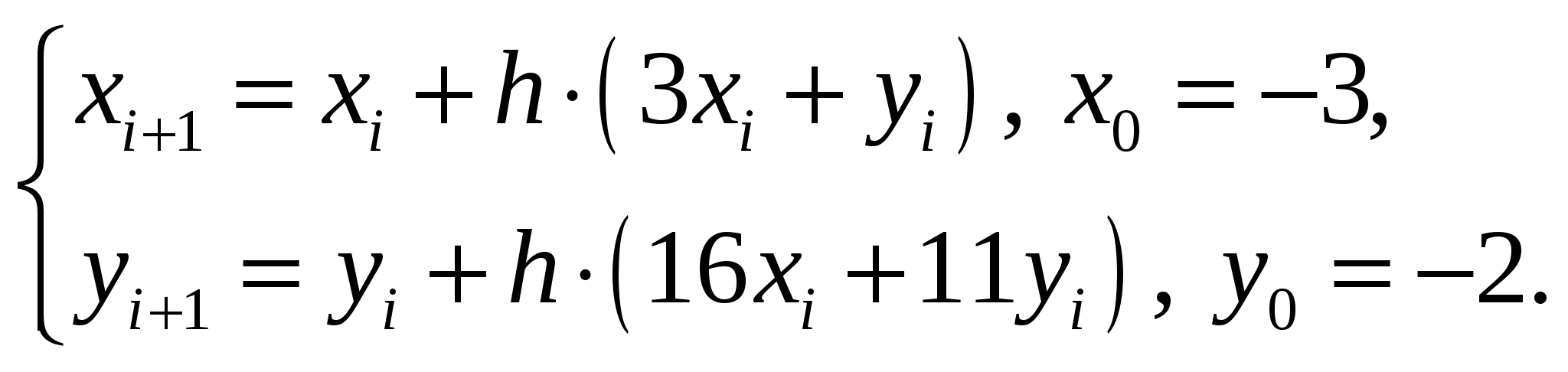

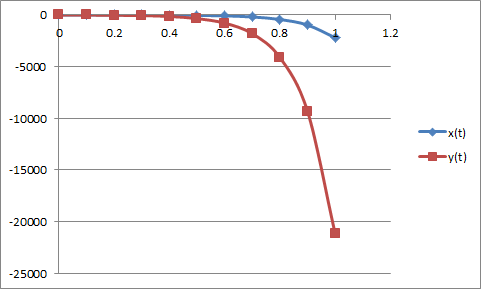i	t	x	y
0	0	-3	-2
1	0.1	-4.1	-9
2	0.2	-6.23	-25.46
3	0.3	-10.645	-63.434
4	0.4	-20.1819	-150.243
5	0.5	-41.2608	-347.802
6	0.6	-88.4193	-796.402
7	0.7	-194.585	-1813.91
8	0.8	-434.352	-4120.56
9	0.9	-976.714	-9348.13
10	1	-2204.54	-21193.8

Исследование на устойчивость

Найдем характеристическое уравнение



Два комплексных корня в правой полуплоскости – неустойчивый фокус.