Теория вероятностей и математическая статистика.. Решение в урне всего 15 шаров. Количество способов вынуть 2 шара из 15 равно Ответ
 Скачать 20.02 Kb. Скачать 20.02 Kb.
|
|
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РЕЙТИНГОВОЙ РАБОТЫ Вариант 4. В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми? Решение: В урне всего 15 шаров. Количество способов вынуть 2 шара из 15 равно: Ответ: Вероятность того, что первым вытащили белый шар p1 = 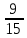 Вероятность того, что вторым вытащили белый шар p2 = 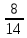 Вероятность того, что оба шара окажутся белыми p=p1 x p2 p = 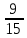 x x 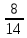 сокращаем дроби p = сокращаем дроби p = 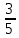 x x 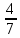 = = 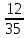 Ответ: Вероятность того, что оба шара окажутся белыми 0,34285. Вариант 4. В студенческой группе организована лотерея. Разыгрываются две вещи стоимостью по 1000 рублей. и одна стоимостью 3000 рублей. Составить закон распределения суммы чистого выигрыша для студента, который приобрел один билет за 100 рублей. Всего продано 50 билетов. Решение: Величина суммы чистого выигрыша, может иметь три значения: - 100 рублей, если студент проиграет 100 рублей, уплаченные им за билет, 900 рублей и 2900 рублей, фактический выигрыш уменьшается на стоимость билета. Первый результат возможен в 47 случаев из 50, второй результат - 2, а третий результат - 1. Поэтому их вероятности таковы: -100, 900, 2900 ; 0,94 0,04 0,02 Возможные события x: х1 - отсутствие выигрыша х2 - выигрыш приза стоимостью 1000 рублей х3 - выигрыш приза стоимостью 3000 рублей Эти события несовместимы и образуют полную систему событий, это значит что сумма вероятностей этих событий равна 1. р(х1) + р(х2) + р(х3) = 1 Вычислим вероятность каждого события: р(х1) = 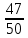 ; р(х1) = 0,94 ; р(х1) = 0,94р(х2) = 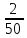 ; р(х2) = 0,04 ; р(х2) = 0,04р(х3) = 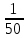 р(х3) =0,02 . р(х3) =0,02 . Ответ: Составим таблицу распределения,
|
