Физика. Решение Вектор ускорения По определению ускорение первая производная скорости по времени

• Название: Решение Вектор ускорения По определению ускорение первая производная скорости по времени
• Анкор: Физика
• Дата: 22.02.2023
• Размер: 277 Kb.
• Имя файла: 5.doc
• Тип: Решение; #950533

1. Материальная точка начинает двигаться из начала координат в момент времени t₀ = 0 с нулевой начальной скоростью и ускорением, изменяющимся со временем по закону , где b=3 м / с² , k = 12м / с ³ . На каком расстоянии от начала координат окажется точка через время t=1 c?
Дано:



b= 3м / с²,

k= 12м / с³

t=1 c





Определить: ∆r

Решение:

Вектор ускорения

По определению ускорение - первая производная скорости по времени.

Соответственно проекции скорости:



Определим координаты х и y.

По определению скорость 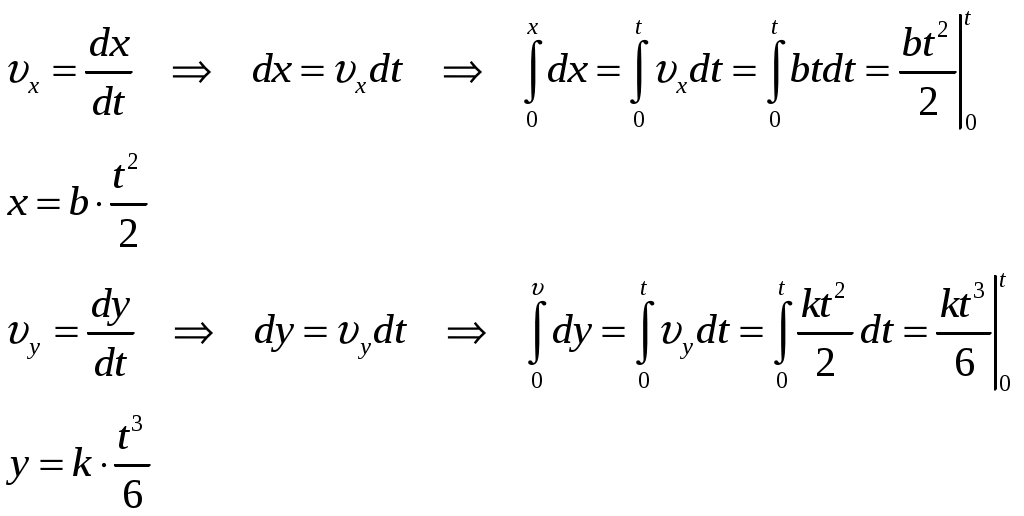, , тогда







Для момента времени t₁=1 c

м
Ответ: м
2. Сформулировать уравнения движения частицы массы m: а) в проекциях на оси x, y, z декартовой системы координат; б) в проекциях на направления касательной и нормали к траектории. Консервативна ли сила ? В случае положительного ответа найти потенциальную энергию U(x,y,z).
Дано:



Найти: U(x,y,z)

Решение:
а) При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями

(1)

эквивалентными векторному уравнению

(2)

Уравнения (1) и соответственно (2) называются кинематическими уравнениями дви­жения материальной точки.





Помимо кинематических уравнений движения материальной точки существуют динамические (или дифференциальные) уравнения движения материальной точки. Уравнение вида:

    (3)

называется векторным дифференциальным уравнением движения материальной точки. – равнодействующая сила, приложенная к материальной точке, - ускорение.

Векторное дифференциальное уравнение эквивалентно трем скалярным дифференциальным уравнениям. Это проекции уравнения (3) на координатные оси:

    (4)

Уравнения (4) – дифференциальные уравнения движения материальной точки в декартовой системе координат. В этих уравнениях x, y, z – текущие координаты точки, – проекции на координатные оси равнодействующих сил, приложенных к материальной точке.

б) В проекции на естественные оси уравнение движения материальной точки в так называемой естественной форме имеет вид:

    или (5)

где – проекция скорости на направление касательной, R— радиус кривизны траектории в текущем положении точки, — проекции равнодействующей силы на касательную, главную нормаль и бинормаль траектории в текущем положении точки, - тангенциальное ускорение, - нормальное ускорение.



2) Консервативные силы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки.

Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.

Если векторное поле задано функцией , то его роторное поле задаётся следующей векторной функцией:



В любой точке потенциального поля  его ротор равен нулю:

В нашем случае , следовательно,

Тогда



Значит, сила является консервативной (потенциальной).

3) Если сила является консервативной, то потенциальная энергия



Потенциальная энергия

3) Определить величины и , соответствующие изменению направления вектора на противоположное.
Дано:


Найти: и
1)



2) модуль вектора ,

3) - изменение модуля вектора .

Так как вектор изменил только направление на противоположное, без изменения длины, то изменение модуля =0

4. Колесо вращается вокруг своей оси симметрии так, что зависимость угла поворота радиуса колеса от времени дается уравнением ϕ = Аt + Bt² + Ct³ , где А=2 рад/с, В=0,5 рад/с ² , С=0,5рад/с³ . Найти радиус R колеса, если в момент времени t=2 c нормальное ускорение точки на ободе колеса равно a_n= 36 м/с ²
Дано:

 = А t + Bt² + Ct³

А=2 рад/с,

В =0,5 рад/с ² ,

С=0,5рад/с³

t=2 c

a_n= 36 м/с ²

Найти:R

Решение:

Нормальное ускорение



Угловая скорость

Тогда радиус окружности .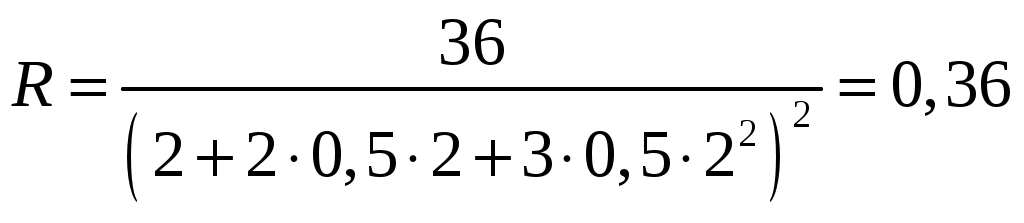

м
Ответ: R=0,36 м

5. Найти для идеального газа уравнение такого процесса, при котором
теплоемкость газа изменяется с температурой по закону С = α /Т , где α = const.

Дано:

С = α /Т ,

α = const

Найти:f(p,V,T)
Решение:

Теплоемкостью называется величина, равная количеству теплоты, которое нужно сообщить веществу, чтобы повысить его температуру на 1 градус.

.

Из первого закона термодинамики:





где dU – изменение внутренней энергии;

- работа расширения газа;

С_V, - молярная теплоемкость при постоянном объеме;

dV - изменение объема газа.

= i/2R, где R- универсальная газовая постоянная.



Из уравнения состояния идеального газа



Разделим правую и левую части на vRT:



Интегрируя, получаем:





Из уравнения Майера R=C_p-C_V

Тогда 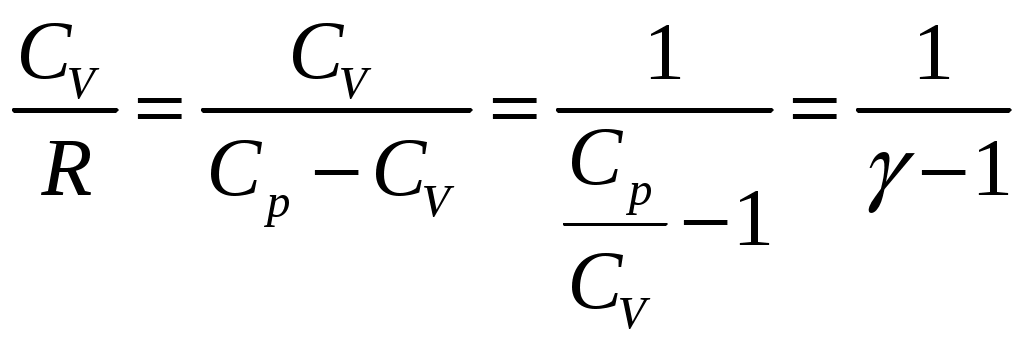, где γ- показатель адиабаты









Окончательно уравнение процесса
Ответ: