Гидравлика курсовая работа. курсовая 1. Изм Лист докум
 Скачать 379.54 Kb.
|
|
С  ОДЕРЖАНИЕ КР 21.03.01.19.12.16 Изм Лист № докум. Подпись Дата Разраб. Габдрахимов А.А Расчет гидравлической циркуляционной установк  иПопова М.Н Пров. Лит Лист Листов 2 30 АГНИ 19-12 Н. контр. Утв. ВВЕДЕНИЕ Гидра́влика — прикладная наука о законах движения, равновесии жидкостей и способах приложения этих законов к решению задач инженерной практики. В отличие от гидромеханики, гидравлика характеризуется особым подходом к изучению явлений течения жидкостей: она устанавливает приближённые зависимости, ограничиваясь во многих случаях рассмотрением одноразмерного движения, широко используя при этом эксперимент, как в лабораторных, так и в натурных условиях. Наряду с этим намечается всё большее сближение между гидромеханикой и гидравликой: с одной стороны, гидромеханика всё чаще обращается к эксперименту, с другой — методы гидравлического анализа становятся более строгими. Некоторые принципы гидростатики были установлены ещё Архимедом, возникновение гидродинамики также относится к античному периоду, однако формирование гидравлики как науки начинается с середины XV века, когда Леонардо да Винчи лабораторными опытами положил начало экспериментальному методу в гидравлике. В XVI—XVII веках С. Стевин, Г. Галилей и Б. Паскаль разработали основы гидростатики как науки, а Э. Торричелли дал известную формулу для скорости жидкости, вытекающей из отверстия. В дальнейшем И. Ньютон высказал основные положения о внутреннем трении в жидкостях. В XVIII веке Д. Бернулли и Л. Эйлер разработали общие уравнения движения идеальной жидкости, послужившие основой для дальнейшего развития гидромеханики и гидравлики. Однако применение этих уравнений (так же как и предложенных несколько позже уравнений движения вязкой жидкости) для решения практических задач привело к удовлетворительным результатам лишь в немногих случаях, в связи с этим с конца XVIII века многие учёные и инженеры опытным путём изучали движение воды в различных частных случаях, в результате чего наука обогатилась значительным числом эмпирических формул. Практическая гидравлика всё более отдалялась от теоретической гидродинамики. Сближение между ними наметилось лишь к концу XIX века в результате формирования новых взглядов на движение жидкости, основанных на исследовании структуры потока. Особо заслуживают упоминания работы О. Рейнольдса, позволившие глубже проникнуть в сложный процесс течения реальной жидкости и в физическую природу гидравлических сопротивлений и положившие начало учению о турбулентном движении. Впоследствии это учение, благодаря исследованиям Л. Прандтля и Т. Кармана, завершилось созданием полуэмпирических теорий турбулентности, получивших широкое практическое применение. К этому же периоду относятся исследования Н. Е. Жуковского, из которых для гидравлики наибольшее значение имели работы о гидравлическом ударе и о движении грунтовых вод. В XX веке быстрый рост гидротехники, теплоэнергетики, гидромашиностроения, а также авиационной техники привел к развитию гидравлики, которое характеризуется синтезом теоретических и эксперементальных методов. Практическое значение гидравлики возросло в связи с потребностями современной техники в решении вопросов транспортирования жидкостей и газов различного назначения и использования их для разнообразных целей. Если ранее в гидравлике изучалась лишь одна жидкость — вода, то в современных условиях всё большее внимание уделяется изучению закономерностей движения вязких жидкостей (нефти и её продуктов), газов, неоднородных и т. н. неньютоновских жидкостей. Меняются и методы исследования и решения гидравлических задач. 1ОПИСАНИЕ ЦИРКУЛЯЦИОННОЙ УСТАНОВКИ Жидкость по самотечному трубопроводу поступает из верхнего резервуара А в нижний резервуар В, откуда насосом перекачивается в промежуточную емкость С и из нее выливается в резервуар А. На всасывающей линии насосной установки имеется всасывающая коробка с обратным клапаном 1, поворотное колено 2, задвижка 3, вакуумметр Рв. На нагнетательной линии установлены манометры  ,  ,  , скоростная трубка 5 и расходомер Вентури 6. Промежуточная емкость С в донной части имеет насадок 7.Таблица 1 – Исходные данные
2 СХЕМА УСТАНОВКИ  Рисунок 1 – Схема циркуляционной установ 3РАСЧЕТ ЦИРКУЛЯЦИОННОЙ УСТАНОВКИ 3.1 Определение геометрической высоты всасывания насоса Для определения геометрической высоты воспользуемся известным уравнением Бернулли. Для его применения необходимо выбрать плоскость сравнения. Плоскостью сравнения может служить любая горизонтальная плоскость. Также необходимо выбрать два сечения. Сечения проводятся перпендикулярно вектору скорости. Нумерация сечений производится по направлению движения жидкости. Уравнение Бернулли для установившегося движения реальной несжимаемой жидкости записывается:  гдеz-расстояние от выбранных сечений соответственно до некоторой произвольно выбранной плоскости сравнения (м). Если сечение лежит ниже плоскости сравнения, то z отрицательна. P - абсолютное или манометрическое давление в сечениях, Па;  - коэффициент кинетической энергии (коэффициент Кориолиса) - характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока. Обычно принимается равным единице, т.к при турбулентном течении стремиться к этому значению.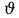 – средняя скорость в сечениях, м/с;g- ускорение свободного падения, м/с²;  - потери напора между сечениями. Они представляют собой сумму потерь напора по длине и сумму потерь напора на местных сопротивлениях: На схеме циркуляционной установкиудобновыбратьдва сечения: где - 1-1 это поверхность жидкости в нижнем резервуаре В; - 2-2 в месте установки вакуумметра Рв во всасывающей линии насосной установки. Тогда уравнение Бернулли для этих сечений запишется в виде:  где  - расстояния от сечений 1-1 и 2-2 соответственно до некоторой произвольно выбранной горизонтальной плоскости; - давления в сечениях 1-1 и 2-2 соответственно;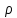 – плотность циркуляционной жидкости;g - ускорение свободного падения;  - скорость течения жидкости в сечении 1-1 и 2-2соответственно; - потери напора на участках между выбранными сечениями.Если выбрать поверхность жидкости в нижнем резервуаре за начало отсчета, т.е. сечение 1-1, тогда  , а  ,Поскольку в нижнем резервуаре (В) уровень установившийся, значение скорости 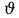будет равным нулю. А так как резервуар открыт, то давление в сечении 1-1 можно принять равным атмосферному . Давление же в сечении 2-2 представляет собой разность атмосферного и вакуумного давления .Коэффициент Кориолиса ( ) принимается равным единице т. к. режим течения – турбулентный. Тогда в уравнении Бернулли остается лишь одна неизвестная величина – скорость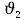 . Скорость определяется по формуле: где Q – расход жидкости, м³/с; S – площадь поперечного сечения, м²; В результате, формула (2) примет вид:  В полученной формуле известны все величины, кроме  . Поэтому для определения геометрической высоты всасывания насоса (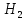 ) предварительно необходимо определить Qи .3.1.1 Определение расхода жидкости Для определения расхода жидкости рассмотрим ртутный дифманометр расходомера Вентури. Запишем уравнение неразрывностидля сечений6-6 и 7-7:  следовательно, (5) Из полученного равенства выразим скорость 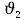: Запишем уравнение Бернулли для двух сечений 6-6 и 7-7:  где  - расстояния от сечений 7-7и 8-8соответственно до некоторой произвольно выбранной горизонтальной плоскости;P - давления в сечениях 7-7и 8-8соответственно; 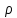- плотность циркулирующей жидкости;g - ускорение свободного падения; 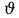-скорость течения жидкости в сечениях 7-7и 8-8соответственно; - силы Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях 7-7и 8-8соответственно; - потери напора на участках между выбранными сечениями.Теоретический расход будет меньше, т.к. существуют потери напора. Учтем это с помощью поправочного коэффициента, который называется коэффициентом расхода μ.  (8)где  =  Подставив, получим:  В итоге имеем:  |
,кг/
,м
,
/c
,м
,м
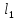,м
,мм
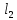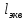,м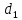
,м
,м
,мм
, мм рт. ст.
,м
,мм
,кг/
,м
,мм
,кПа
,м
,мм
,кПа
,м
,мм
,м
