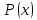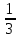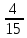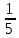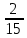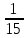Задачи по теории вероятностей. Задачи. Решение Вероятности того, что случайно выбранная деталь была произведена на старой и новой линии равны соответственно
 Скачать 29.78 Kb. Скачать 29.78 Kb.
|
|
1. Предприниматель производит одинаковые детали на двух производственных линиях. Две пятых продукции сходит со старой линии, при этом 10% выпуска признается браком. Остальные три пятых продукции производятся на новейшей линии, для которой процент брака равен лишь 4%. Какова вероятность того, что оказавшаяся бракованная деталь была выпущена на старой производственной линии? Решение: Вероятности того, что случайно выбранная деталь была произведена на старой и новой линии равны соответственно: 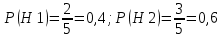 Условные вероятности того, что деталь, выпущенная на соответствующей линии, - бракованная, равны: 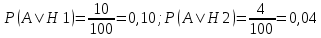 По формуле полной вероятности находим вероятность того, что что случайно выбранная деталь окажется бракованной: 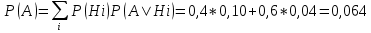 И вероятность того, что оказавшаяся бракованная деталь была выпущена на старой производственной линии, находим по формуле Байеса: 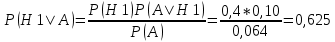 2. Известно, что 60% щенков собак определенной породы имеют черные глаза. Цвет глаз одного щенка не зависит от цвета глаз другого. Какова вероятность того, что в помете из девяти щенков по крайней мере одна треть будет иметь черные глаза? Решение: Вероятность того, что щенок имеет глаза черного цвета: 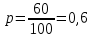 Т.к. цвет глаз одного щенка не зависит от цвета глаз другого, и вероятность иметь глаза черного цвета – постоянна, то имеем испытания по схеме Бернулли, вероятности в которой находятся по одноименной формуле: 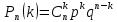 В нашем случае 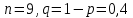 . .Находим вероятности того, что в помете из девяти щенков только у 0, 1 и 2 щенков будут глаза черного цвета: 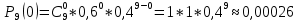 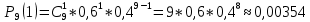 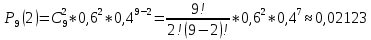 И вероятность того, что в помете из девяти щенков по крайней мере одна треть будет иметь черные глаза как вероятность события, противоположного событию «из девяти щенков менее трети будет иметь черные глаза»: 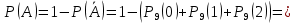 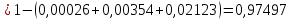 3. Студенты Артемов и Белов стоят в очереди в раздевалку. Всего в очереди 6 человек. Случайная величина 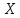 – число студентов, стоящих между ними. – число студентов, стоящих между ними. 1) Составить таблицу распределения 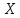 . .2) Найти математическое ожидание 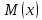 и дисперсию и дисперсию 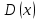 . .3) Построить график функции распределения 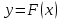 . .4) Найти вероятность 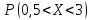 . .Решение: Количество способов, которыми можно расставить 6 человек в очередь равно числу перестановок из 6 человек. Число студентов, стоящих между Артемовым и Беловым, может принимать значение от 0 до 4. Вычислим соответствующие вероятности: - 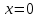 . «Объединяя» двух выбранных студентов, получаем очередь из пяти элементов. Число способов в этом случае равно произведению числа перестановок из пяти «студентов» и числа перестановок из двух «объединенных» студентов (они также могут идти друг за другом в произвольном порядке), т.е.: . «Объединяя» двух выбранных студентов, получаем очередь из пяти элементов. Число способов в этом случае равно произведению числа перестановок из пяти «студентов» и числа перестановок из двух «объединенных» студентов (они также могут идти друг за другом в произвольном порядке), т.е.: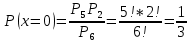 - 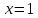 . Имеем четыре возможных размещения по местам в очереди: 1 и 3, 2 и 4, 3 и 5, 4 и 6. Поэтому число способов равно произведению числа перестановок из четырех «невыбранных» студентов, числа перестановок из двух «выбранных» и числа четыре – возможные способы «бронирования» мест в очереди, т.е.: . Имеем четыре возможных размещения по местам в очереди: 1 и 3, 2 и 4, 3 и 5, 4 и 6. Поэтому число способов равно произведению числа перестановок из четырех «невыбранных» студентов, числа перестановок из двух «выбранных» и числа четыре – возможные способы «бронирования» мест в очереди, т.е.: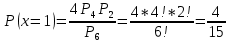 Остальные вероятности вычисляем из аналогичных соображений: 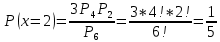 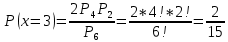 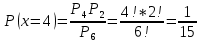 Проверяем правильность вычислений: 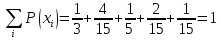 Получили следующую таблицу распределения 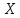 : :
Вычислим числовые характеристики: - математическое ожидание: 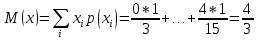 - дисперсия: 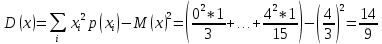 Вероятность того, что случайная величина примет значение из заданного интервала: 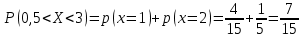 Функция распределения выражает вероятность того, случайная величина примет значение, меньшее 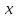 : :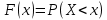 Поэтому имеем: 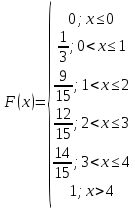 Графически: 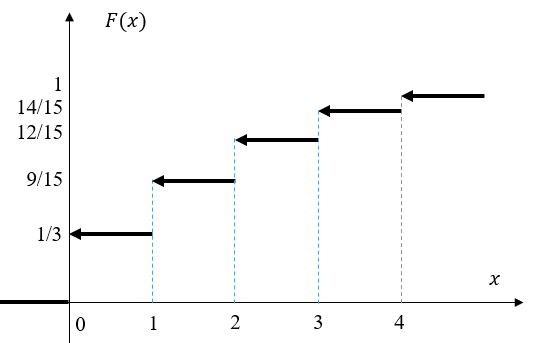 4. Считая, что 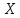 – нормально распределенная случайная величина, которая задается функцией плотности распределения – нормально распределенная случайная величина, которая задается функцией плотности распределения 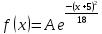 , найти , найти 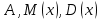 , , 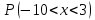 . .Решение: Плотность нормально распределенной случайной величины с параметрами 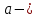 математическим ожиданием и математическим ожиданием и 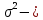 дисперсией имеет вид: дисперсией имеет вид: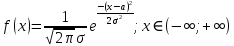 Т.е. в нашем случае математическое ожидания и дисперсия равны соответственно: 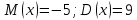 А неизвестный коэффициент 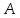 : :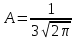 Т.е. функция плотности распределения имеет вид: 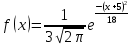 Вероятность того, что нормально распределенная случайная величина примет значение из интервала 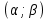 равна: равна: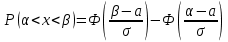 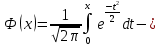 функция Лапласа, значения которой протабулированы. функция Лапласа, значения которой протабулированы.Тогда: 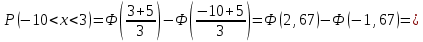 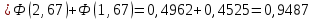 |