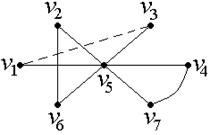
Комбинаторика. Применение графовых моделей Вариант 3. Решение задач по теории графов Вариант 3 Задание Определить Эйлерову цепь в неориентированном графе G, изображенном на рисунке. Решение

• Название: Решение задач по теории графов Вариант 3 Задание Определить Эйлерову цепь в неориентированном графе G, изображенном на рисунке. Решение
• Анкор: Комбинаторика. Применение графовых моделей Вариант 3
• Дата: 23.12.2022
• Размер: 82.04 Kb.
• Имя файла: 3.docx
• Тип: Решение; #860144
• страница: 1 из 5

3. Решение задач по теории графов


Вариант 3
Задание 1. Определить Эйлерову цепь в неориентированном графе G, изображенном на рисунке.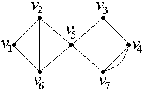



Решение:
Найдем Эйлерову цепь в неориентированном графе G, изображенном на рис. 10.

Прежде, чем приступать к нахождению Эйлеровой цепи, необходимо проверить степени вершин графа G − согласно утверждению 2, для существования Эйлеровой цепи, необходимо и достаточно, чтобы в графе G ровно 2 вершины нечетной степени.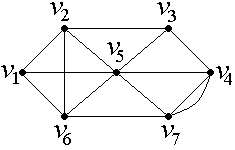



Рис. 10.

В рассматриваемом графе нечетные степени имеют вершины V3 и V1 (степень этих вершин равна 3). Соединяя эти вершины фиктивным ребром так, как показано на рис. 11, получаем граф G¢: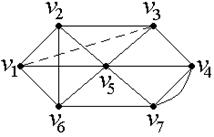



Рис. 11.

Поскольку в конечном итоге будет получена цепь, то очевидно, что началом и концом этой цепи будут вершины с нечетными степенями. Поэтому, следуя описанному выше алгоритму, будем циклы mI так, чтобы хотя бы один из них начинался или кончался на вершинах V3 или V1.

Пусть цикл m1 составят ребра, проходящие через следующие вершины: V3 V4 V7 V6 V1 V2 V3. Согласно алгоритму, удаляем из G¢Все ребра, задействованные в цикле m1. Теперь граф G’ будет таким, как показано на рис. 12.

Составляем следующий цикл m2: V4 V5 V6 V2 V5 V7 V4. Граф G¢ после удаления ребер, составляющих цикл m2, изображен на рис. 13.

Рис.12	Рис. 13

Очевидно, что последний цикл m3 будет состоять из V3 V5 V1|V3, где последнее ребро, соединяющее вершины V1 и V3 – фиктивно. После удаления ребер, составляющих цикл m3, в графе G¢ не останется ни одного ребра.

Теперь по общим вершинам склеиваем полученные циклы. Поскольку m1 и m2 имеют общую вершину V4, то, объединяя их, получим следующий цикл: V3 V4 V5 V6 V2 V5 V7 V4 V7 V6 V1 V2 V3. Теперь склеим получившийся цикл с циклом m3: V3 V4 V5 V6 V2 V5 V7 V4 V7 V6 V1 V2 V3 V5 V1|V3. Удаляя фиктивное ребро, получаем искомую Эйлерову цепь: V3 V4 V5 V6 V2 V5 V7 V4 V7 V6 V1 V2 V3 V5 V1.



Задание 2.
Применяя метод ветвей и границ, решить задачу коммивояжера с матрицей расстояний: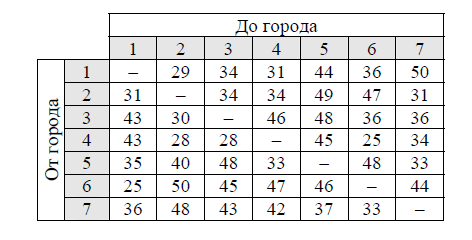




Решение:

Возьмем в качестве произвольного маршрута:
X₀ = (1,2);(2,3);(3,4);(4,5);(5,6);(6,7);(7,1)
Тогда F(X₀) = 29 + 34 + 46 + 45 + 48 + 44 + 36 = 282
Для определения нижней границы множества воспользуемся операцией редукции или приведения матрицы по строкам, для чего необходимо в каждой строке матрицы D найти минимальный элемент.
d_i = min(j) d_ij

i j	1	2	3	4	5	6	7	di
1	-	29	34	31	44	36	50	29
2	31	-	34	34	49	47	31	31
3	43	30	-	46	48	36	36	30
4	43	28	28	-	45	25	34	25
5	35	40	48	33	-	48	33	33
6	25	50	45	47	46	-	44	25
7	36	48	43	42	37	33	-	33

Затем вычитаем d_i из элементов рассматриваемой строки. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.

i j	1	2	3	4	5	6	7
1	-	0	5	2	15	7	21
2	0	-	3	3	18	16	0
3	13	0	-	16	18	6	6
4	18	3	3	-	20	0	9
5	2	7	15	0	-	15	0
6	0	25	20	22	21	-	19
7	3	15	10	9	4	0	-

Такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент:
d_j = min(i) d_ij

i j	1	2	3	4	5	6	7
1	-	0	5	2	15	7	21
2	0	-	3	3	18	16	0
3	13	0	-	16	18	6	6
4	18	3	3	-	20	0	9
5	2	7	15	0	-	15	0
6	0	25	20	22	21	-	19
7	3	15	10	9	4	0	-
dj	0	0	3	0	4	0	0