лаба №3. санктпетербургский горный университе т
 Скачать 91.11 Kb. Скачать 91.11 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра Общей и технической физики (лаборатория виртуальных экспериментов) Отчет по лабораторной работе №3
Оценка: ____________ Дата: ________
Санкт-Петербург 2022 1. Цель работы. Определить ускорение свободного падения при помощи универсального маятника. 2. Краткое теоретическое содержание. 1) Явление, изучаемое в работе. Ускорение свободного падения. 2) Определения основных физических понятий. Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести. Момент инерции твердого тела относительно оси вращения – это сумма моментов инерции материальных точек, из которых состоит это тело. Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. 3) Законы и соотношения, описывающие изучаемые процессы, на основании которых, получены расчётные формулы. Теореме Штейнера Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния d между осями.  4) Пояснения к физическим величинам и их единицы измерений. l – длина маятника, м g – свободного падения, м/с^2 J – момент инерции маятника относительно оси качаний (точки подвеса), кг*м^2 m- масса, кг J0- момент инерции маятника относительно оси, проходящей через его цент масс, кг*м^2 n – число колебаний t – время, с Т – период, с ΔT– погрешность изменения периода, с Δl– погрешность измерения длины нити математического маятника, мм ΔL– погрешность измерения приведенной длины физического маятника, мм 3. Схема установки.  Универсальный маятник. 1 - основание универсального маятника; 2 – математический маятник; 3 – винт; 4 – верхний кронштейн;.5 – винт; 6 – диски; 7 - колонка; 8 - оборотный маятник; 9 – нижний кронштейн; 10 - фотоэлектрический датчик; 11 – секундомер. С1 и С2 – призмы (ножи). 4. Расчётные формулы.   – ускорение свободного падения для математического маятника. – ускорение свободного падения для математического маятника. – ускорение свободного падения для оборотного маятника. – ускорение свободного падения для оборотного маятника. 5. Формулы для расчёта погрешностей косвенных измерений.  - Средняя квадратическая ошибка косвенных измерений для g измеренного при помощи математического маятника. - Средняя квадратическая ошибка косвенных измерений для g измеренного при помощи математического маятника. - Средняя квадратическая ошибка косвенных измерений для g измеренного при помощи оборотного маятника. - Средняя квадратическая ошибка косвенных измерений для g измеренного при помощи оборотного маятника.6. Таблицы с результатами измерений и вычислений. I. Математический маятник
II. Оборотный маятник. t1=12,186 c t1=12,189 c t1=12,185 c 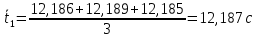 ; t2=12,182 c ; t2=12,182 c 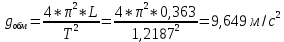 7. Пример вычисления (для одного опыта). Математический маятник  9,812м/c^2 9,812м/c^2l=0,431 м t5=13,166 c n=10 Δl=0,001 м ΔT=0,001 с 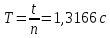 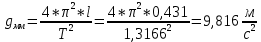  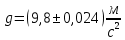 Оборотный маятник L=0,363 м T=1,2187 с 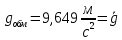   8. Графический материал.   9. Анализ полученного результата. Выводы. В данной лабораторной работе экспериментальным путем было определено ускорение свободного падения с помощью математического маятника и физического маятника. Полученные результаты в ходе работы с математическим маятником почти совпадают с истинным значение ускорения свободного падения, что говорит о крайней точности расчетной формулу и о незначительных погрешности приборов, а результат полученный при экспериментировании с оборотным маятник довольно сильно расходиться с истинным, что говорит, скорее всего, о сильной погрешности в приборах. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
