отчёт. Отчет по лабораторной работе 8 определение ускорения свободного падения при помощи универсального маятника
 Скачать 233 Kb.
|
|
Федеральное агентство по образованию Российской Федерации  Кафедра общей и технической физики СПГГИ (ТУ) им. Г.В. ПлехановаОтчетпо лабораторной работе №8 определение ускорения свободного падения при помощи универсального маятника Выполнил: студент группы ЭР-08-1 Фадин Д.А. Проверил: ________ преподаватель Чернобай В.И. СПб 2008 Цель работы – определить ускорение свободного падения при помощи универсального маятника. Краткое теоретическое обоснование. 1. Явление, которое наблюдается в работе – колебания математического, оборотного и физического маятников. 2. Математический маятник – материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Физический маятник - абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести. Метод оборотного маятника основан на том, что в каждом физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника на одну и другую период колебаний неизменится. Момент инерции маятника (J) относительно оси вращения есть физическая величина, равная сумме произведения масс N материальных точек системы на квадраты их расстояний до рассматриваемой оси.  Масса (m) – физическая величина являющаяся одной из характеристик материи, определяющая ее инерционные и гравитационные свойства. Период вращения (T) – время, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2  . Ускорение свободного падения(g)- ускорение с которым движется любое тело в поле тяготения Земли, если на него действует только сила тяжести   g является постоянной величиной и равно 9,8  3. Момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через его центр масс тела,сложенного с произведением массы тела на квадрат расстояния  между осями: Физический маятник, отклоненный на малый угол от положения равновесия, совершает гармонические колебания. Так как  ,  циклическая частота колебаний ( ), то для периода колебаний физического маятника получаем следующую формулу:  где  момент инерции физического маятника.Следовательно, период гармонических колебаний физического маятника зависит от момента инерции маятника и ускорения свободного падения g. Обозначим  . Величина lпр называется приведенной длиной физического маятника, под которой понимается длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника. Тогда период колебаний физического маятника можно записать следующим образом: 4. Теоретически ожидаемый результат измерений: g=9,8  Схема установки. 1 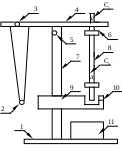 -основание универсального маятника 2- математический маятник 3- винт 4- верхний кронштейн 5- винт 6-диск 7- колонка 8- оборотный маятник 9- нижний кронштейн 10- фотоэлектрический датчик 11 - универсальный электронный секундомер С1 и С2 - призмы Расчетные формулы.   – период колебаний математического маятника,l – длина маятникa, g – ускорение свободного падения;  – период колебаний физического маятника,J– момент инерции маятника, m – масса, l – расстояние от центра тяжести до оси, L- приведенная длина; J1 = J0+ ml2 (теорема Штейнера), J0– момент инерции маятника относительно оси, проходящей через его центр масси параллельно оси качения. T = t/N – определение периода; g = 4π2 ·  /T2; g = gср   - окончательный результат.Формулы погрешностей косвенных измерений.   Таблицы с результатами измерений и вычислений. математический маятник Таблица А
оборотный маятник Таблица Б
Пример вычисления. 1. Исходные данные: таблица А и таблица Б 2.1. Вычисления для математического маятника: 1) T=  =13,568/10=1,3469 с g= =4*3,142*0,439/1,35682 9,414 2) T= =13,564/10=1,3564 с g= =4*3,142*0,439/1,35642 9,419 3) T= =13,566/10=1,3566 с g= =4*3,142*0,439/1,35662 9,417 4) T= =13,565/10=1,3565 с g= =4*3,142*0,439/1,35652 9,418 5) T= =13,564/10=1,3564 с g= =4*3,142*0,439/1,35642 9,419 6) T= =13,562/10=1,3562 с g= =4*3,142*0,439/1,35622 9,422 7) T= =13,564/10=1,3564 с g= =4*3,142*0,439/1,35642 9,419 8) T= =13,562/10=1,3562 с g= =4*3,142*0,439/1,35622 9,422 9) T= =13,565/10=1,3565 с g= =4*3,142*0,439/1,35652 9,418 10) T= =13,563/10=1,3563 с g= =4*3,142*0,439/1,35632 9,421 2.2. Вычисления для оборотного маятника: T= =12,454/10=1,2454 с g= =4*3,142*0,400/1,24542 10,170 T= =12,485/10=1,2942 с g= =4*3,142*0,400/1,24852 10,120 Расчет погрешностей эксперимента: Для математического маятника: 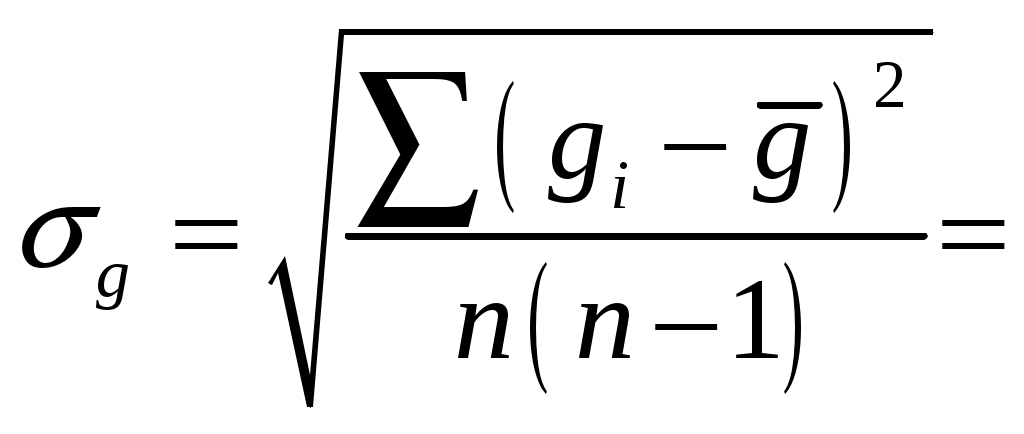 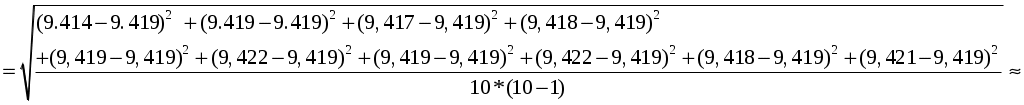=   ≈0,00076739 Для оборотного маятника: 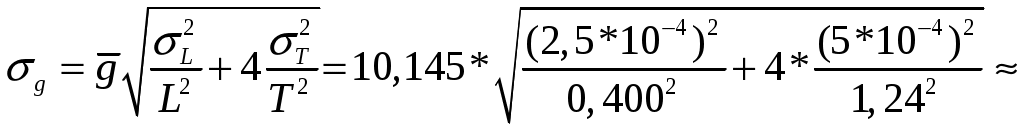=  0,1035 3. Окончательные результаты: 1)  =( ) 2) =( ) Вывод: В лабораторной работе было определено ускорение свободного падения g при помощи универсального маятника. Полученное значение имеет расхождения с табличным значением, что говорит об возможных ошибках при измерении. Вероятно, при более точных измерениях вычисление ускорения свободного падения g получилось бы более схожим с табличным. По ходу работы можно сделать вывод, что измерение ускорения свободного падения g с помощью маятников сводится к следующему: измерению периодов маятников T и расстоянию между призмами L, а так же определению длины маятника и вычислению по формуле ускорения свободного падения  . После всех измерений на двух типах маятников и последующих расчетах получено два значения ускорения свободного падения: g= и g= |