ТОЭ практическая работа. СТ_Сценарий практической работы_5_ПЕРЕХОДНЫЕ_ПРОЦЕССЫ_2_КЛАССИКА. Сценарий практической работы 5 по дисциплине Теоретические основы электротехники

• Название: Сценарий практической работы 5 по дисциплине Теоретические основы электротехники
• Анкор: ТОЭ практическая работа
• Дата: 08.05.2022
• Размер: 2.68 Mb.
• Имя файла: СТ_Сценарий практической работы_5_ПЕРЕХОДНЫЕ_ПРОЦЕССЫ_2_КЛАССИКА.docx
• Тип: Сценарий; #517250
• страница: 1 из 5

Сценарий практической работы № 5

по дисциплине «Теоретические основы электротехники» по направлению 13.03.02 Электроэнергетика и электротехника.

Группа ЭЭ-18-Д(4-й семестр)
Раздел 7 Переходные процессы в цепях с сосредоточенными параметрами

Классический метод.

Второй закон коммутации

Введение (5-10мин.)
Цель работы: Отработать навыки решения уравнений переходных процессов по второму закону коммутации в цепях с сосредоточенными параметрами классическим методом.
Общие теоретические сведения
В линейных электрических цепях наряду с установившимися режимами работы имеют место переходные электромагнитные процессы, происходящие при переходе от одного установившегося режима цепи к другому.

Переходные процессы в линейных электрических цепях описываются линейными дифференциальными уравнениями. При этом ток или напряжение определяются общим интегралом соответствующего дифференциального уравнения со свободным членом. Общий интеграл уравнения представляет собой сумму частного решения этого уравнения и решения того же уравнения без свободного члена.

Переходящие, или свободные, составляющие тока i_св и напряжения u_св, определяемые решением дифференциального уравнения без свободного члена, с течением времени стремятся к нулю.

В результате частного решения дифференциального уравнения можно получить установившиеся, или принужденные составляющие тока и напряжения i_у, и_у, имеющие место при установившемся режиме, т. е. при законченном переходном процессе.

При этом ток и напряжение переходного процесса в электриче­ской цепи могут быть записаны как суммы: i_пер = i_у + i_св; u_пер = u_y + и_св. В общий интеграл дифференциального уравнения входят постоянные интегрирования, число которых определяется порядком соответствующего уравнения. Переходные процессы в неразветвленной электрической цепи с параметрами R, L и С описываются дифференциальным уравнением для мгновенных значений напряжений, составленным по второму закону Кирхгофа:



После дифференцирования имеем уравнение вида:



Для определения принужденной (установившейся) составляющей i_у тока переходного процесса, когда воздействующая функция u{t) постоянная или является периодической, необходимо найти его значение в установившемся режиме.

Переходную (свободную) составляющую i_св тока находят в результате решения дифференциального уравнения без свободного члена:



При этом соответствующее характеристическое уравнение приводится к виду: Lp² = Rp +1/С = 0. Корни этого уравнения:



Свободная составляющая тока переходного процесса:

i_CB(t) = A₁е^p1t + A₂e^p2t.

Ток переходного процесса:

i_пер(0) = i_y(t) +i_СВ(t).

Аналогичным образом можно определить напряжение и другие электрические и магнитные величины на любом участке линейной электрической цепи в переходном режиме.

При включении электрической цепи с R и L под постоянное напряжение (рисунке 1) переходный процесс описывается дифферен­циальным уравнением, записанным по второму закону Кирхгофа для цепи при установке переключателя П из положения 1 в положение 2:



Характеристическое уравнение, соответствующее полученному диф­ференциальному уравнению, имеет вид: R+Lp= 0, где p = -R/L - корень характеристического уравнения.

С учетом этого выражение для свободной составляющей тока переходного процесса приводят к виду:

i_CB(t) = Aе^pt = A₂e^-Rt/L.

где А - постоянная интегрирования; е - основание натурального логарифма.

Так как воздействующее на электрическую цепь напряжение u(t) постоянно, значение принужденной составляющей тока цепи в переходном режиме оказывается равным его установившемуся значению: i_у = U/R. Ток в цепи при переходном процессе:

Постоянную интегрирования А определяют из начальных условий. Так как в цепи с индуктивностью ток не может измениться скачком, то при i_y = 0 ток в цепи равен нулю: i(0)= U/R + A = 0. Отсюда A = -U/R, тогда:

i_CB = -U/Re^-Rt/L.

С учетом этого выражение для тока переходного процесса при­обретает вид: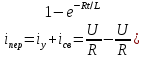

)= ).

где τ = L/R - постоянная времени цепи, равная промежутку времени, по истечении которого свободная составляющая тока в цепи изменяется в е раз по сравнению со своим исходным значением.

Напряжение переходного процесса на индуктивности L, уравно­вешивающее ЭДС самоиндукции, определяют из уравнения:



При коротком замыкании RL-цепи, присоединенной к источнику постоянного напряжения U, переключатель П из положения 2 устанавливается в положение 3, в цепи возникает переходный про­цесс, обусловленный наличием запаса энергии в магнитном поле катушки с индуктивностью L. Происходящий переходный процесс характеризуется свободным током, так как i_у = 0; в результате: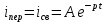

=

Постоянную интегрирования А определяют исходя из условия, что до момента короткого замыкания ток в цепи: i₍₀₎ = I = U/R = A.

С учетом этого ток переходного процесса:

=

Аналогично изменяется в данной цепи и напряжение: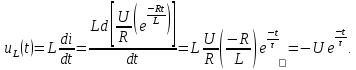



Второй закон коммутации
Второй закон коммутации
В рассматриваемой цепи (рисунок 2) ток:


Рисунок 1
В рассматриваемой цепи ток:



В результате дифференциальное уравнение приводится к виду:



Ему соответствует характеристическое уравнение: RСp + 1 = 0, где корень характеристического уравнения p = -1/RC.

Решение дифференциального уравнения без свободного члена относительно напряжения на конденсаторе позволяет определить свободную составляющую этого напряжения:



где А - постоянная интегрирования, определяемая исходя из принятых начальных условий u_с(0) = 0.

Напряжение и_Су на обкладках конденсатора в установившемся режиме определяют в результате частного решения соответствующе­го дифференциального уравнения цепи. В установившемся режиме ток в цепи /_у = 0, следовательно, u_Cy = u(t)=U и напряжение на конденсаторе во время переходного процесса:



Постоянную интегрирования А находят из начальных условий. Напряжение на конденсаторе до включения u_с(0) = 0, так как к моменту включения цепи конденсатор С не был заряжен:

При этом и_с(0) = U+A = 0, откуда:



Временная зависимость напряжения на обкладках конденсатора во время переходного процесса описывается уравнением: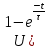

)= ).

где τ = RС - постоянная времени.

Ток в цепи при переходном процессе:



=

Короткое замыкание неразветвленной RС-цепи (рисунок 1), ранее находившейся под постоянным напряжением U = const, осуществляется установкой переключателя П (в момент времени t = 0) из положения 2 в положение 3 (в положении 1 схема отключена). Электромагнитные процессы в цепи с момента ее замыкания происходят за счет энергии, равной 1/2CU², сосредоточенной к этому моменту времени в электрическом поле конденсатора, которая в течение переходного процесса преобразуется в теплоту, рассеиваемую резистором R.

Для установившихся значений тока в RС-цепи и напряжения на об­кладках конденсатора С при переходном процессе имеем: i_y = 0, а и_Су= 0.

При этом свободные составляющие тока в цепи и напряжения на конденсаторе:

;

Ток в цепи и напряжение на обкладках конденсатора в переход­ном режиме: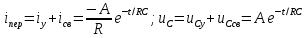


Постоянную интегрирования А определяют из начальных условий. При t = 0 напряжение на обкладках конденсатора равно U, т. е. u_с(0) = U = A. При этом для переходных значений тока и напряжения на конденсаторе справедливы уравнения: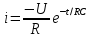

=-

При расчете переходных процессов в линейных разветвленных электрических цепях для определения токов в отдельных ветвях и напряжений на участках цепи записывают соответствующее число уравнений, составленных по первому и второму законам Кирхгофа. При получении характеристического уравнения необязательно приводить полученную систему уравнений к одному уравнению относительно одной неизвестной функции.

Система однородных дифференциальных уравнений, записанных для свободных составляющих токов в ветвях разветвленной цепи, записывается в виде соответствующей системы алгебраических уравнений и в отличие от исходной системы не содержит производных интегралов. В этой системе уравнений производные свободной составляющей тока di_CB/dt заменяют символом pi_CB, а интеграл от этого тока J /_св dt -символом i_cJp (где р - корень характеристического уравнения - показатель затухания, одинаковый для всех свободных составляющих токов цепи). Действительно, если i_ct = Ae^pl, то производная от свободного тока di_cJdt=d(Ae^p,)/dt=pAe^p'=pi_CB, а интеграл:

=A

Постоянная интегрирования при этом оказывается равной нулю, так как свободные составляющие не содержат не зависящих от времени слагаемых. Подобный переход от системы линейных дифференциальных уравнений к системе алгебраических, называемый алгебраизацией системы дифференциальных уравнений, для свободных токов значительно упрощает составление характеристического уравнения. Из полученной системы алгебраических уравнений составляется затем определитель Δ(р), который должен равняться нулю, так как данная система уравнений имеет решение, отличное от нулевого, если определитель системы равен нулю.

Выражение для Δ(р) = 0 и является характеристическим уравнением, в котором единственным неизвестным является его корень р. Составить характеристическое уравнение системы однородных дифференциальных уравнений (уравнение без свободного члена) можно и другим путем. Для этого записывают выражение комплексного входного сопротивления Z(jωt) для соответствующей цепи, в котором jω заменяют символ р. Полученное обобщенное сопротивление приравнивают к нулю. Уравнение Z(p) = 0 и будет характеристическим уравнением данной цепи.

Число корней характеристического уравнения определяется его степенью. Если это уравнение имеет п корней, общее решение системы однородных дифференциальных уравнений имеет вид: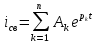



где р_к - корни уравнения, А_к - постоянные интегрирования.

Для нахождения постоянных интегрирования необходимо решить систему уравнений для искомого свободного тока i_CB(t), соответствующих моменту времени t= 0. В качестве недостающих (п - 1) уравнений используются уравнения, полученные путем (п - 1)-кратного дифференцирования уравнения для свободного тока i_CB(t).

В рассматриваемой цепи (рисунок 2) ток:

.



Рисунок 2
В результате дифференциальное уравнение приводится к виду:


Ему соответствует характеристическое уравнение: RСp + 1 = 0, где корень характеристического уравнения p = -1/RC.

Решение дифференциального уравнения без свободного члена относительно напряжения на конденсаторе позволяет определить свободную составляющую этого напряжения:

=

где А - постоянная интегрирования, определяемая исходя из принятых начальных условий u_с(0) = 0.

Напряжение и_Су на обкладках конденсатора в установившемся режиме определяют в результате частного решения соответствующе­го дифференциального уравнения цепи. В установившемся режиме ток в цепи /_у = 0, следовательно, u_Cy = u(t)=U и напряжение на конденсаторе во время переходного процесса: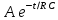

=



Постоянную интегрирования А находят из начальных условий. Напряжение на конденсаторе до включения u_с(0) = 0, так как к моменту включения цепи конденсатор С не был заряжен:

При этом и_с(0) = U+A = 0, откуда:



Временная зависимость напряжения на обкладках конденсатора во время переходного процесса описывается уравнением:



u_cгде τ = RС - постоянная времени.

Ток в цепи при переходном процессе:



Короткое замыкание неразветвленной RС-цепи, ранее находившейся под постоянным напряжением U = const, осуществляется установкой переключателя П (в момент времени t = 0) из положения 2 в положение 3 (в положении 1 схема отключена). Электромагнитные процессы в цепи с момента ее замыкания происходят за счет энергии, равной 1/2CU², сосредоточенной к этому моменту времени в электрическом поле конденсатора, которая в течение переходного процесса преобразуется в теплоту, рассеиваемую резистором R.

Для установившихся значений тока в RС-цепи и напряжения на об­кладках конденсатора С при переходном процессе имеем: i_y = 0, а и_Су= 0.

При этом свободные составляющие тока в цепи и напряжения на конденсаторе: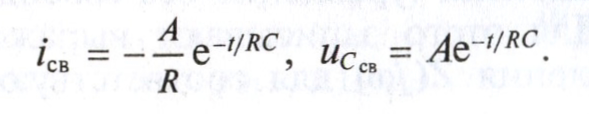



Ток в цепи и напряжение на обкладках конденсатора в переход­ном режиме:



Постоянную интегрирования А определяют из начальных условий. При t = 0 напряжение на обкладках конденсатора равно U, т. е. u_с(0) = U = A. При этом для переходных значений тока и напряжения на конденсаторе справедливы уравнения:



При расчете переходных процессов в линейных разветвленных электрических цепях для определения токов в отдельных ветвях и напряжений на участках цепи записывают соответствующее число уравнений, составленных по первому и второму законам Кирхгофа. При получении характеристического уравнения необязательно приводить полученную систему уравнений к одному уравнению относительно одной неизвестной функции.

Система однородных дифференциальных уравнений, записанных для свободных составляющих токов в ветвях разветвленной цепи, записывается в виде соответствующей системы алгебраических уравнений и в отличие от исходной системы не содержит производных интегралов. В этой системе уравнений производные свободной составляющей тока di_CB/dt заменяют символом pi_CB, а интеграл от этого тока J /_св dt -символом i_cJp (где р - корень характеристического уравнения - показатель затухания, одинаковый для всех свободных составляющих токов цепи). Действительно, если i_ct = Ae^pl, то производная от свободного тока di_cJdt=d(Ae^p,)/dt=pAe^p'=pi_CB, а интеграл:



Постоянная интегрирования при этом оказывается равной нулю, так как свободные составляющие не содержат не зависящих от времени слагаемых. Подобный переход от системы линейных дифференциальных уравнений к системе алгебраических, называемый алгебраизацией системы дифференциальных уравнений, для свободных токов значительно упрощает составление характеристического уравнения. Из полученной системы алгебраических уравнений составляется затем определитель Δ(р), который должен равняться нулю, так как данная система уравнений имеет решение, отличное от нулевого, если определитель системы равен нулю.

Выражение для Δ(р) = 0 и является характеристическим уравнением, в котором единственным неизвестным является его корень р. Составить характеристическое уравнение системы однородных дифференциальных уравнений (уравнение без свободного члена) можно и другим путем. Для этого записывают выражение комплексного входного сопротивления Z(jωt) для соответствующей цепи, в котором jω заменяют символ р. Полученное обобщенное сопротивление приравнивают к нулю. Уравнение Z(p) = 0 и будет характеристическим уравнением данной цепи.

Число корней характеристического уравнения определяется его степенью. Если это уравнение имеет п корней, общее решение системы однородных дифференциальных уравнений имеет вид:



где р_к - корни уравнения, А_к - постоянные интегрирования.

Для нахождения постоянных интегрирования необходимо решить систему уравнений для искомого свободного тока i_CB(t), соответствующих моменту времени t= 0. В качестве недостающих (п - 1) уравнений используются уравнения, полученные путем (п - 1)-кратного дифференцирования уравнения для свободного тока i_CB(t).