Шпаргалка по МАТАН. ответы матан. Случайным событием

• Название: Случайным событием
• Анкор: Шпаргалка по МАТАН
• Дата: 26.05.2021
• Размер: 0.52 Mb.
• Имя файла: ответы матан.doc
• Тип: Документы; #209988

1. 
   Классификация событий. Классическое определение вероятности.
   

Геометрическое определение вероятности.

Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.

Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.

Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.

Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.

Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами или элементарными событиями. Исход называется благоприятствующим появлению события А, если появление этого исхода влечет за собой появление события А.

Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу

P(A)=m/n

Свойство 1. Вероятность достоверного события равна единице
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.

Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие A – это подмножество этой области, пространства элементарных исходов G.

Если для простоты считать, что все точки G «равноправны» (выбор точек равномерен внутри области), то вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.

Геометрическая вероятность события А определяется отношением:

P(A)=m(A)/m(G),

где m(G), m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно.

Чаще всего, в одномерном случае речь будет идти о длинах отрезков, в двумерном - о площадях фигур, в трехмерном - об объемах тел.

2. 
   Действия над событиями. Алгебра событий. Несовместные события. Теорема о
   

вероятности суммы произвольных событий, несовместных событий. Теорема о вероятности произведения произвольных событий, независимых событий.

Теорема сложения вероятностей. Вероятность того, что произойдёт одно из двух взаимно несовместных событий, равна сумме вероятностей этих событий:

Вероятности противоположных событий обычно обозначают малыми буквами p и q. В частности,



из чего следуют следующие формулы вероятности противоположных событий:

и  .

Два случайных события называются совместными, если наступление одного события не исключает наступления второго события в том же самом наблюдении. 

Теорема сложения вероятностей для совместных событий. Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей. Формула вероятностей совместных событий имеет следующий вид:



Если события А и В несовместны, то их совпадение является невозможным случаем и, таким образом, P(AB) = 0. Четвёртая формула вероятности для несовместных событий такова:



Теорема умножения вероятностей для независимых событий. Вероятность одновременного наступления двух независимых событий А и В  равна произведению вероятностей этих событий и вычисляется по формуле:

 

Если наступление одного события влияет на вероятность наступления второго события, то события называют взаимно зависимыми.

Если события А и В взаимно зависимы, то условной вероятностью  называют вероятность события В, принимая, что событие А уже наступило

Теорема умножения вероятностей взаимно зависимых событий. Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого, то есть вычисляется по формуле:



или

3. 
   Формула полной вероятности. Формула Байеса.
   

Формула полной вероятности позволяет найти вероятность события A, которое может наступить только с каждым из n исключающих друг друга событий  , образующих полную систему, если известны их вероятности  , а условные вероятности события A относительно каждого из событий системы равны  .

,

Поэтому формула Байеса представляет собой отношение произведения вероятности одного из событий системы на условную вероятность этого события относительно соответствующего события системы к полной вероятности наступления события A с учётом всех событий системы.

.

4. 
   Схема Бернулли, формула Бернулли. Функция Лапласа, ее свойства.
   

Интегральная и локальная формулы Муавра-Лапласа.

Каждое событие наступает в каждом испытании с одной и той же вероятностью, которая не изменяется, если становятся известными результаты предыдущих испытаний. Такие испытания называются независимыми, а схема называется схемой Бернулли. Предполагается, что такие испытания могут быть повторены как угодно большое количество раз.



Функция Ф(х) табулирована. Для применения этой таблицы нужно знать свойства функции Лапласа:

1) Функция Ф(х) нечетная: Ф(-х)= -Ф(х).

2) Функция Ф(х) монотонно возрастающая.

3) Ф(0)=0.

4) Ф(+)=0,5; Ф(-)=-0,5. На практике можно считать, что при х5 функция Ф(х)=0,5; при х-5 функция Ф(х)=-0,5.

Пусть в каждом из   независимых испытаний событие A может произойти с вероятностью  ,   (условия схемы Бернулли). Обозначим как и раньше, через   вероятность ровно   появлений события А в   испытаниях. кроме того, пусть  – вероятность того, что число появлений события А находится между   и  .

Локальная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

 где   - функция Гаусса (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Интегральная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

P(n; k1, k2)  где  - функция Лапласа (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:

а) 

б) при больших   верно  .

Теоремы Лапласа дают удовлетворительное приближение при  . Причем чем ближе значения   к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).

5. 
   Дискретные и непрерывные случайные величины (ДСВ и НСВ). Закон
   

распределения ДСВ.

 Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Выпадение некоторого значения случайной величины Х это случайное событие: Х = х_i. Среди случайных величин выделяют дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно

Законом распределения дискретной случайной величины называют соответствие между полученными значениями дискретной случайной величины и их вероятностями. Его можно задать:

1) таблично (рядом распределения);

2) графически;

3) аналитически (в виде формулы).

6. 
   Математическое ожидание ДСВ, свойства.
   

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных её значений на вероятности этих значений:

Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений xi , которые принимает СВ Х, на соответствующие вероятности pi:M(X)=∑xi⋅pi.

Свойство 1. Математическое ожидание постоянной величины равно этой постоянной:



Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:



Свойство 3. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:



Свойство 4. Математическое ожидание произведения случайных величин равно произведению их математических ожиданий:



Свойство 5. Если все значения случайной величины X уменьшить (увеличить) на одно и то же число С, то её математическое ожидание уменьшится (увеличится) на то же число:

7. 
   Дисперсия ДСВ, свойства.
   

Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения её от математического ожидания:



Средним квадратическим отклонением   случайной величины X называется арифметическое значение квадратного корня её дисперсии:

.

Свойство 1. Дисперсия постоянной величины равна нулю:

.

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:

.

Свойство 3. Дисперсия случайной величины равна математическому ожиданию квадрата этой величины, из которого вычтен квадрат математического ожидания самой величины:

,

где  .

Свойство 4. Дисперсия суммы (разности) случайных величин равна сумме (разности) их дисперсий:

8. 
   Функция распределения НСВ, свойства. Могут ли функции: а) ,
   

б) 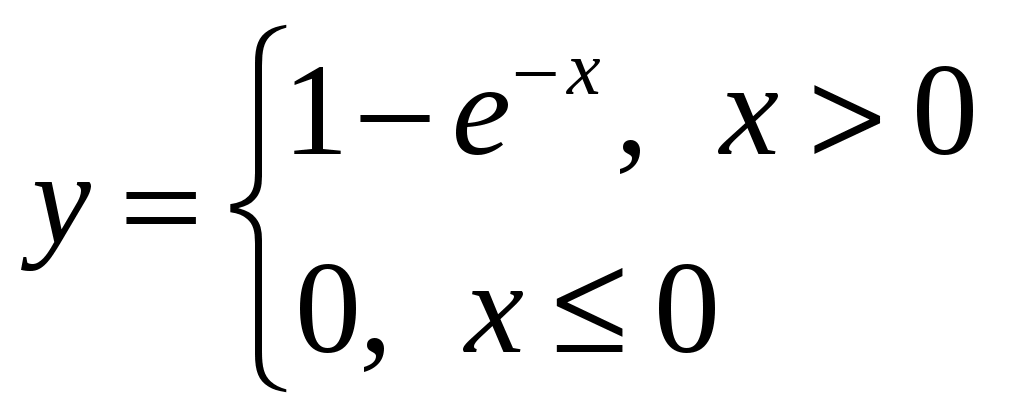, в) быть функциями распределения некоторой НСВ?

Функция распределения непрерывной случайной величины   определяется точно так же, как и функция распределения ДСВ:

 – вероятность того, что случайная величина   примет значение, МЕНЬШЕЕ, чем переменная  , которая «пробегает» все значения от «минус» до «плюс» бесконечности. Таким образом, учитываются все значения, которые В ПРИНЦИПЕ может принять произвольная случайная величина. С увеличением   функция распределения «накапливает» (суммирует) вероятности, а значит, является неубывающей и изменяется в пределах  . По этой причине её иногда называют интегральной функцией распределения.

Важной особенностью является тот факт, что функция распределения ЛЮБОЙ непрерывной случайной величины всегда и всюду непрерывна! Часто её можно встретить в кусочном виде, например: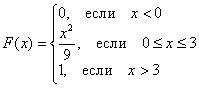

9. 
   Плотность распределения вероятности НСВ, свойства. Могут ли функции:
   

а) 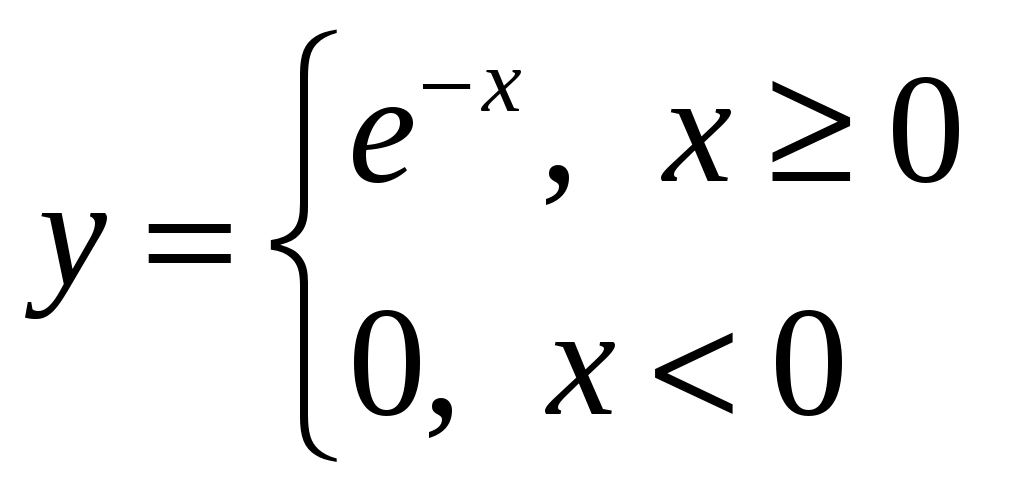, б) , в) быть плотностью распределения некоторой НСВ? Числовые характеристики НСВ.

Плотностью распределения φ(x) непрерывной случайной величины называется первая производная от функции распределения вероятности F(x).
Свойство 1: Функция φ(x) плотности распределения неотрицательна

Свойство 2: Несобственный интеграл от функции плотности распределения пределах от −∞ до +∞ равен 1.

Свойство 3: Любая неотрицательная функция f(x)≥0, удовлетворяющая равенству ∫−∞+∞f(x)dx=1 является функцией плотность распределения некоторой непрерывной случайной величины.
Определение 1. Математическим ожиданием непрерывной случайной величины x с плотностью распределения f(x) называется выражение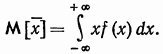


Определение 2. Дисперсией случайной величины x называется математическое ожидание квадрата соответствующей центрированной случайной величины:



Определение 3. Среднеквадратичным отклонением случайной величины x называется корень квадратный из дисперсии:

10. 
    Связь между функцией распределения и плотностью вероятности случайной величины.
    

Плотностью вероятности f(x) непрерывной случайной величины называется производная её функции распределения:

11. 
    Основные законы распределения:
    

- биномиальный,

Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.



- закон Пуассона,

Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:



где

   λ = np = const
   n - число испытаний, стремящиеся к бесконечности
   p - вероятность наступления события, стремящаяся к нулю
   m - число появлений события А
- равномерный,

Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.

- показательный,

Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид: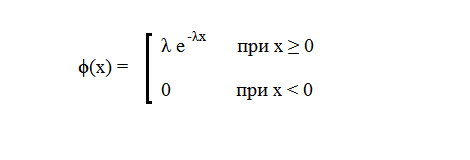



где λ - параметр обратно-пропорциональный математическому ожиданию.

- нормальный.

   Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид:



   где 
   а - математическое ожидание случайной величины
   σ - среднее квадратическое отклонение

12. 
    Совместные распределения случайных величин. Закон распределения
    

случайной точки дискретного типа на плоскости.

Функция     называется функцией распределения вектора   или функцией  совместного распределения случайных величин  .

13. 
    Закон распределения случайной точки непрерывного типа на плоскости.
    

Необходимое и достаточное условие независимости случайных величин (Х, У).

14. 
    Ковариация двух случайных величин. Коэффициент корреляции.
    

Ковариацией (или корреляционным моментом) К_ху случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

, Или  ,

Где  , .

Из определения следует, что  . Кроме того, .

т.е. ковариация СВ с самой собой есть ее дисперсия.

Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих величин:

.

Из определения следует, что  . Очевидно также, что коэффициент корреляции есть безразмерная величина.

Свойства коэффициента корреляции:

1. 
   Коэффициент корреляции принимает значения на отрезке [-1;1], т.е.  .
   
2. 
   Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е.  .
   

15. 
    Неравенство Чебышева.
    

P(|X−M(X)|≥a)≤D(X)a2,a>0.P(|X−M(X)|≥a)≤D(X)a2,a>0.

Также его можно записать в другой форме:

P(|X−M(X)|1−D(X)a2,a>0.P(|X−M(X)|1−D(X)a2,a>0.

Неравенство Чёбышева показывает, что случайная величина принимает значения близкие к среднему (математическому ожиданию) и дает оценку вероятности больших отклонений.

16. 
    Сходимость по вероятности. Закон больших чисел в форме Чебышева.
    

Говорят, что случайная величина   сходится по вероятности к величине  , если при увеличении   вероятность того, что   и   будут сколь угодно близки, неограниченно приближается к единице, а это значит, что при достаточно большом 

,

где   - произвольно малые положительные числа.

Запишем в аналогичной форме теорему Чебышева. Она утверждает, что при увеличении   среднее арифметическое   сходится по вероятности к  , т. е.

17. 
    Теорема Бернулли.
    

Теорема Бернулли. Если в каждом из независимых испытаний вероятность появления события постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Другими словами, если сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

18. 
    Центральная предельная теорема.
    

Теорема. Если   - независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием   и дисперсией  , то при неограниченном увеличении   закон распределения суммы

                           неограниченно приближается к нормальному.


Задачи для подготовки к экзамену
1. Одновременно бросают 2 игральные кости, на гранях которых нанесены очки 1, 2, 3, 4, 5, 6. Какова вероятность того, что сумма очков, выпавших на двух костях, равна восьми?( )

2. В коробке содержится 6 одинаковых занумерованных кубиков. Наудачу по одному извлекают все кубики из коробки. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.( )

3. В ящике имеется 15 деталей, 10 из которых окрашены. Сборщик наудачу извлек 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными. ( )

4. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 5 отличников.( )

5. Десять студентов условились ехать с определенным электропоездом, но

не договорились о вагоне. Какова вероятность того, что ни один из них не встретится с другим, если в составе электропоезда 10 вагонов. Предполагается, что все возможности в распределении студентов по вагонам равновероятны.( )

6. Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0,7. При изготовлении такой же детали на втором станке эта вероятность равна 0,8. На первом станке изготовлены две детали, на втором – три. Найти вероятность того, что все детали первосортные.( )

7. Сколько надо бросить игральных костей, чтобы с вероятностью, меньшей 0,3, можно было ожидать, что ни на одной из выпавших граней не появится 6 очков?

( )

8. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор срабатывает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает: а) только один сигнализатор; б) хотя бы один сигнализатор. (а) ; б) )

9. Дана система S. Блоки, обозначенные одинаковыми буквами, одинаковы; все блоки независимы. Вычислить надежность системы (вероятность безотказной работы в течение определенного времени), если известны надежность блоков: . ( )



10. Два стрелка независимо один от другого делают по два выстрела (каждый по своей мишени). Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,6, для второго -0,7. Выигравшим соревнование считается тот стрелок, в мишени которого будет больше пробоин. Найти вероятность того, что выиграет первый стрелок.( )

11. Из урны, содержащей 2 белых и один черный шар, перекладывают шар в урну, содержащую два черных и один белый шар. Определить вероятность извлечь черный шар из второй урны после указанного перекладывания.( )

12. Вероятности попадания при каждом выстреле для трех стрелков равны соответственно . При одновременном выстреле всех трех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок.( )

13. По линии связи возможна передача кода 1234 с вероятностью 0,6 и кода 4321 с вероятностью 0,4. Код высвечивается на табло, которое может исказить цифры. Вероятность принятия 1 за 1 равна 0,8, а 1 за 4 равна 0,2. Вероятность принятия 4 за 4 равна 0,9, а 4 за 1 равна 0,1. Вероятности принятия 2 за 2 и 3 за 3 равна 0,7. Вероятности принятия 2 за 3 и 3 за 2 равны 0,3. Оператор принял код 4231. Определить вероятность того, что был передан код: а) 1234, б) 4321.(а) ; б) )

14. Принимая одинаково вероятным рождение мальчика и рождение девочки, найти вероятность того, что в семье, имеющей 5 детей: а) два мальчика; б) мальчиков больше, чем девочек.(а) ; б) )

15. Среди вырабатываемых деталей бывает в среднем 4% брака. Какова вероятность того, что среди взятых на испытание 5 деталей будет 40% бракованных?( )

16. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найти наиболее вероятное число опоздавших из 855 пассажиров и вероятность этого числа.( , )

17. На прядильной фабрике работница обслуживает 750 веретён. При вращении веретена пряжа рвется в случайные моменты времени из-за неравномерности натяжения, неровности и других причин. Считая, что вероятность обрыва пряжи на каждом из веретён в течение некоторого промежутка времени равна 0,008, найти вероятность того, что за это время произойдет не более 10 обрывов.( )

18. В партии из 10 деталей имеются 8 стандартных. Наудачу отобраны 2 детали. Составить закон распределения числа стандартных деталей среди отобранных. Найти математическое ожидание и среднее квадратичное отклонение стандартных деталей.( )

19. Непрерывная случайная величина имеет плотность распределения



а) Найти коэффициент А; б) построить график плотности распределения ;

в) найти вероятность попадания случайной величины в интервал ;

г) найти функцию распределения ; д) найти математическое ожидание и дисперсию.

(а) ; в) ; г) )

д) .

20. Производится три выстрела с вероятностями попадания в цель, равными . Найти математическое ожидание общего числа попаданий.( )

21. Случайная величина имеет биномиальный закон распределения с числовыми характеристиками . Определить вероятность попадания случайной величины на отрезок .( )

22. Известно, что в партии деталей имеется 10 % бракованных. Найти закон распределения случайной величины - числа годных деталей из пяти, выбранных наудачу. Определить числовые характеристики этого закона .( )

23. Число частиц, излученных радиоактивным элементом в течение произвольного промежутка времени, имеет распределение Пуассона с параметром . Найти вероятность того, что число частиц, излученных за две секунды, будет заключено в отрезке .( )

24. Дистанция между двумя соседними самолетами в строю имеет показательное распределение, причем . Опасность столкновения самолетов возникает при уменьшении дистанции до . Найти вероятность того, что возникает опасность столкновения самолетов в воздухе.( )

25. Цена деления шкалы амперметра равна А. Показания амперметра определяют до ближайшего целого деления. Найти вероятность того, что при отсчете сделана ошибка, превышающая А.( )

26. Нагрузка на стержень подчиняется нормальному закону распределения с числовыми характеристиками . Усилие, разрушающее стержень, составляет . Найти вероятность разрушения стержня.( )

27. Станок-автомат изготовляет валики, контролируя их диаметр . Считая, что распределен нормально, , найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.( )

28. На основе заданного распределения случайной точки (Х, У) найти:

1) одномерные законы распределения случайных величин Х, У и их числовые характеристики;

2) коэффициент корреляции случайных величин Х, У.

У Х	1	2	3
2	0,16	0,10	0,28
3	0,14	0,20	0,12