Сравнение выборочных средних. 2. Сравнение выборочных средних_feb08d6dcfc294be18bea3a241887983. Сравнение выборочных средних Пример
 Скачать 130.76 Kb.
|
|
Сравнение выборочных средних Пример. Время на производство одной детали по первой технологии (с): 27, 28, 29, 27, 28, 29, 31, 32, 30, 29. Время на производство одной детали по второй технологии (с): 28, 29, 27, 28, 29, 32, 31, 33. Доверительная вероятность 95%. Можно ли сделать вывод, что время на производство одной детали в этих технологиях различается? Выдвинем гипотезы: Н0: время на производство одной детали в этих технологиях одинаково. Н1: время на производство одной детали в этих технологиях различается. Укажем время на производство одной детали в ячейках А1:А11 и В1:В9: 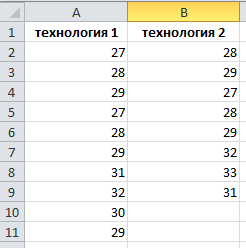 Сначала надо выяснить, различаются ли в технологиях 1 и 2 неизвестные дисперсии. Данные  Анализ данных Двухвыборочный F-тест для дисперсии Ок.Откроется диалоговое окно, которое нужно заполнить:  В графе Интервал переменной 1 указывается ссылка на ячейки, содержащие значения первой выборки. В графе Интервал переменной 2 указывается ссылка на ячейки, содержащие значения второй выборки. В графе альфа указывается уровень значимости 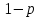 . В нашем случае это 0,05. Также указываются параметры вывода (выходной интервал, новый рабочий лист, новая рабочая книга). 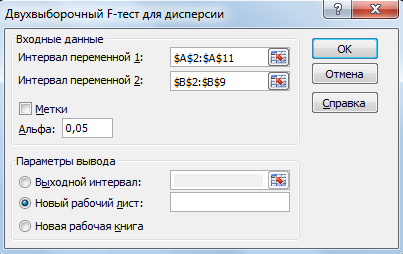 При нажатии кнопки Ок откроется итоговое окно:  Так как в графе P(F<=f) одностороннее указано величина, большая выбранного Альфа (0,223150144>0,05), то принимаем заключение о том, что неизвестные дисперсии не различаются. Воспользуемся двухвыборочным t-тестом с одинаковыми дисперсиями. Вернемся на Лист 1. Данные Анализ данных Двухвыборочный t-тест с одинаковыми дисперсиями Ок.Заполняем раскрывшееся диалоговое окно: 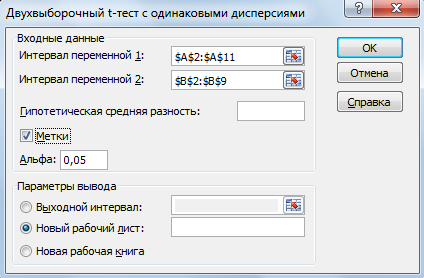 На новом рабочем листе откроется итоговое окно:  Так как Р(Т<=t) двухстороннее больше заданного альфа, то гипотеза Н0 принимается на уровне значимости 0,05. Время на производство одной детали в этих технологиях одинаково. Замечание. Если Двухвыборочный F-тест для дисперсии покажет различие дисперсий (в графе P(F<=f) одностороннее указано величина, меньшая выбранного Альфа), то необходимо воспользоваться двухвыборочным t-тестом с различными дисперсиями. Данные Анализ данных Двухвыборочный t-тест с различными дисперсиями Ок.Задание 1 Время на производство одной детали по первой технологии (с): 37, 39, 42, 37, 41, 42, 41, 40, 41, 39,38. Время на производство одной детали по второй технологии (с): 39, 37, 36, 42, 41,36, 37, 39,38. Доверительная вероятность 0,95. Можно ли сделать вывод, что время на производство одной детали в этих технологиях различается? Задание 2 В двух группах учащихся — экспериментальной и контрольной — получены следующие результаты по учебному предмету (тестовые баллы; см. табл.). Результаты эксперимента
Проверьте гипотезу: Н0: средние тестовые баллы по учебному предмету в экспериментальной и контрольной группах совпадают. |