контрольная. Сущность математического программирования 5 1 Линейное программирование 5
 Скачать 93.77 Kb. Скачать 93.77 Kb.
|
ОГЛАВЛЕНИЕВВЕДЕНИЕ 3 ГЛАВА 1. СУЩНОСТЬ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ 5 1.1 Линейное программирование 5 1.2 Формулировка задачи 6 1.3 Основные понятия линейной алгебры и выпуклого анализа, применяемые в теории математического программирования 7 ГЛАВА 2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 17 2.1. Симплексный метод решения задач линейного программирования 17 25 2.2 Графический метод решения задач линейного программирования 25 ЗАКЛЮЧЕНИЕ 31 СПИСОК ЛИТЕРАТУРЫ 32 ВВЕДЕНИЕЛинейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать. Актуальность настоящей работы обусловлена, с одной стороны, большим интересом к теме «Линейное программирование» в современной науке, с другой стороны, ее недостаточной разработанностью. Рассмотрение вопросов связанных с данной тематикой носит как теоретическую, так и практическую значимость. Для решения задач линейного программирования потребовалось создание специальных методов. В данной курсовой работе будет рассмотрен геометрический метод решения задач линейного программирования. Геометрический метод применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно. Объектом исследования является раздел математического программирования – линейное программирование. Предметом исследования выступают задачи линейного программирования и методы их решения. Таким образом, целью данной курсовой работы является: освоить навыки использования геометрического метода для решения задач линейного программирования. Для этого были поставлены следующие задачи: 1) изучить теоретические сведения, необходимые для решения задач линейного программирования геометрическим методом. 2) разобрать алгоритм решения ЗЛП геометрическим методом. 3) решить поставленные задачи, используя рассмотренный метод решения задач линейного программирования. Структура курсовой работы. В соответствии с целью, задачами и логикой исследования работа состоит из введения, две главы, заключения, списка литературы. ГЛАВА 1. СУЩНОСТЬ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ1.1 Линейное программированиеЛинейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.1 Линейное программирование является частным случаем математического программирования. Одновременно оно - основа нескольких методов решения задач целочисленного и нелинейного программирования. Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их. Термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Математическая формулировка задачи линейного программирования 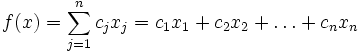 Нужно максимизировать  при условиях при i = 0, 1, 2, . . . , m . Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя ее во всех остальных равенствах и неравенствах (а также в функции f). Такую задачу называют «основной» или «стандартной» в линейном программировании.2 |
