контрольная. Сущность математического программирования 5 1 Линейное программирование 5

• Название: Сущность математического программирования 5 1 Линейное программирование 5
• Анкор: контрольная
• Дата: 17.01.2023
• Размер: 93.77 Kb.
• Имя файла: 337227f.docx
• Тип: Документы; #891148
• страница: 2 из 4

1.2 Формулировка задачи

Даны линейная функция Z=С₁х₁+С₂х₂+...+С_Nx_N (1.1) и система линейных ограничений:
a₁₁x₁ + a₂₂x₂ + ... + a_1NХ_N = b₁

a₂₁x₁ + a₂₂x₂ + ... + a_2NХ_N = b₂

. . . . . . . . . . . . . . .

a_i1x₁ + a_i2x₂ + ... + a_iNХ_N = b_i (1.2)

. . . . . . . . . . . . . . .

a_M1x₁ + a_M2x₂ + ... + a_MNХ_N = b_M

x_j 0 (j = 1, 2, ... ,n) (1.3)
где а_ij, b_j и С_j - заданные постоянные величины.

Найти такие неотрицательные значения х₁, х₂, ..., х_n, которые удовлетворяют системе ограничений (1.2) и доставляют линейной функции (1.1) минимальное значение.

Общая задача имеет несколько форм записи.

Векторная форма записи. Минимизировать линейную функцию Z = СХ при ограничениях А₁х₁ + А₂x₂ + ... + А_Nx_N = А_о, X₀ (1.4)

где С = (с₁, с₂, ..., с_N); Х = (х₁, х₂, ..., х_N); СХ - скалярное произведение; векторы A₁ = A₂ = ,..., A_N состоят соответственно из коэффициентов при неизвестных и свободных членах.

Матричная форма записи. Минимизировать линейную функцию, Z = СХ при ограничениях АХ = А₀Х₀, где С = (с₁, с₂, ..., с_N) - матрица-cтрока; А = (а_ij) - матрица системы; Х =(x_ij)- матрица-столбец, А₀ = (а_i) матрица-столбец

Запись с помощью знаков суммирования. Минимизировать линейную функцию Z = С_jх_j при ограничениях

0пределение 1. Планом или допустимым решением задачи линейного программирования называется Х = (х₁, х₂, ..., х_N), удовлетворяющий условиям (1.2) и (1.3).

0пределение 2. План Х = (х₁, х₂, ..., х_N) называется опорным, если векторы А (i = 1, 2, ..., N), входящие в разложение (1.4) с положительными коэффициентами х , являются линейно независимыми.

Так как векторы А являются N-мерными, то из определения опорного плана следует, что число его положительных компонент не может превышать М.

0пределение 3. Опорный план называется невырожденным, если он содержит М положительных компонент, в противном случае опорный план называется вырожденным.

0пределение 4. Оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наименьшее (наибольшее) значение линейной функции.

В дальнейшем рассмотрено решение задач линейного программирования, связанных с нахождением минимального значения линейной функции. Там, где необходимо найти максимальное значение линейной функции, достаточно заменить на противоположный знак линейной функции и найти минимальное значение последней функции. Заменяя на противоположный знак полученного минимального значения, определяем максимальное значение исходной линейной функции.

1.3 Основные понятия линейной алгебры и выпуклого анализа, применяемые в теории математического программирования

Кратко напомним некоторые фундаментальные определения и теоремы линейной алгебры и выпуклого анализа, которые широко применяются при решении проблем как линейного, так и нелинейного программирования.

Фундаментальным понятием линейной алгебры является линейное (вещественное) пространство. Под ним подразумевается множество некоторых элементов (именуемых векторами или точками), для которых заданы операции сложения и умножения на вещественное число (скаляр), причем элементы, являющиеся результатом выполнения операций, также в соответствии с определением должны принадлежать исходному пространству.

Частными случаями линейных пространств являются вещественная прямая, плоскость, геометрическое трехмерное пространство.

Вектор λ₁a¹ + λ₂a² + …+ λ_ma^m называется линейной комбинацией векторов а¹ а²,..., а^m с коэффициентами λ₁, λ_2, λ_m,

Система векторов линейного пространства а¹ а²,..., а^m называется линейно зависимой, если существуют такие числа λ₁, λ_2, λ_m не равные одновременно нулю, что их линейная комбинация λ₁a¹ + λ₂a² + …+ λ_ma^m равняется нулевому вектору (вектору, все компоненты которого равны нулю). В противном случае систему а¹, а²,..., а^m называют линейно независимой, т. е. линейная комбинация данных векторов может быть равна нулевому вектору только при нулевых коэффициентах λ₁, λ_2, …, λ_m

Максимально возможное количество векторов, которые могут образовывать линейно независимую систему в данном линейном пространстве, называют размерностью пространства, а любую систему линейно независимых векторов в количестве, равном размерности, — базисом пространства.

Линейное пространство обычно обозначают как Rⁿ, где n — его размерность.

Любое подмножество данного линейного пространства, которое само обладает свойствами линейного пространства, называется линейным подпространством. Множество Н, получаемое сдвигом некоторого линейного подпространства L € Rⁿ на вектор a € Rⁿ: H=L+a, называется аффинным множеством (пространством). Если фундаментальным свойством любого линейного пространства или подпространства является принадлежность ему нулевого вектора, то для аффинного множества это не всегда так. На плоскости примером подпространства является прямая, проходящая через начало координат, а аффинного множества — любая прямая на плоскости. Характеристическим свойством аффинного множества является принадлежность ему любой прямой, соединяющей две любые его точки. Размерность аффинного множества совпадает с размерностью того линейного подпространства, сдвигом которого оно получено.

Если рассматривается некоторое линейное пространство Rⁿ, то принадлежащие ему аффинные множества размерности 1 называются прямыми, а размерности (n-1)—гиперплоскостями. Так, обычная плоскость является гиперплоскостью для трехмерного геометрического пространства R³, а прямая — гиперплоскостью для плоскости R². Всякая гиперплоскость делит линейное пространство на два полупространства.

Множество V векторов (точек) линейного пространства Rⁿ называется выпуклым, если оно содержит отрезок прямой, соединяющей две его любые точки, или, другими словами, из того, что a €V и b€V , следует, что х = (1- λ) х а+ λ х b € V , где 0 ≤ λ ≤ 1.

Линейная комбинация векторов а¹, а²... а^m называется выпуклой, если λ_i ≥0, i €1:m и

Множество, содержащее все возможные выпуклые комбинации точек некоторого множества М, называют выпуклой оболочкой данного множества. Можно показать, что выпуклая оболочка множества М является наименьшим выпуклым множеством, содержащим М.

Выпуклая оболочка конечного множества точек называется выпуклым многогранником, а непустое пересечение конечного числа замкнутых полупространств — многогранным выпуклым множеством. В отличие от выпуклого многогранника последнее может быть неограниченным.³

Точка v выпуклого множества V называется его угловой (крайней) точкой, если она не является внутренней точкой ни для какого отрезка, концы которого принадлежат множеству V. Угловые точки выпуклого многогранника являются его вершинами, а сам он — выпуклой оболочкой своих вершин.

Множество К называется конусом с вершиной в точке x₀, если x₀ € К , и из того, что некоторая точка х принадлежит К ( х € К ), следует, что в К содержится и луч, начинающийся в х₀ и проходящий через х, т. е.:



или


Выпуклая оболочка конечного множества лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке.

Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = 3.

Наиболее наглядна эта интерпретация для случая n = 2, т.е. для случая двух переменных x₁ и x₂. Пусть нам задана задача линейного программирования в стандартной форме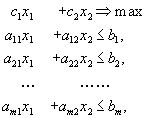

(1.5)


Возьмём на плоскости декартову систему координат и каждой паре чисел (x₁,x₂)поставим в соответствие точку на этой плоскости.

Обратим прежде всего внимание на ограничения x₁ ≥0 и x₂ ≥ 0. Они из всей плоскости вырезают лишь её первую четверть (см. рис. 1). Рассмотрим теперь, какие области соответствуют неравенствам вида a₁ x₁ + a₂ x₂ ≤ b. Сначала рассмотрим область, соответствующую равенству a₁ x₁ + a₂ x₂ = b. Как Вы, конечно, знаете, это прямая линия. Строить её проще всего по двум точкам.⁴

Пусть b ≠ 0. Если взять x₁ = 0, то получится x₂ = b/a₂. Если взять x₂ = 0, то получится x₁ = b/a₁. Таким образом, на прямой лежат две точки (0, b/a₂) и (b/a₁, 0). Дальше через эти две точки можно по линейке провести прямую линию (рисунок 2).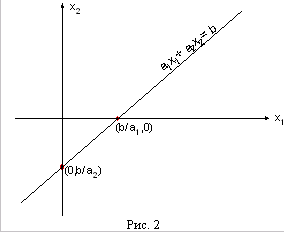

Если же b=0, то на прямой лежит точка (0,0). Чтобы найти другую точку, можно взять любое отличное от нуля значение x₁ и вычислить соответствующее ему значение x₂.

Эта построенная прямая разбивает всю плоскость на две полуплоскости. В одной её части a₁x₁ + a₂x₂ < b, а в другой наоборот a₁x₁ + a₂x₂ > b. Узнать, в какой полуплоскости, какой знак имеет место проще всего посмотрев, какому неравенству удовлетворяет какая-то точка плоскости, например, начало координат, т.е. точка (0,0).

Рассмотрим задачу ЛП в стандартной форме записи:
max f(X) = с₁х₁ + с₂х₂ + ... + с_пх_п (*)
при ограничениях
а
(**)
₁₁х₁ + а₁₂х₂ + … + а_1nх_n ≤ b₁

а₂₁х₁ + а₂₂х₂ + … + а_2nх_n ≤ b₂

……………………………..

а
(***)
_m1х₁ + а_m2х₂ + … + а_mnх_n ≤ b_m

х_j ≥ 0, j = 1, 2, …, n.
Рассмотрим эту задачу на плоскости, т.е. при п = 2. Пусть система неравенств (**), (***) совместна (имеет хотя бы одно решение):
а₁₁х₁ + а₁₂х₂ ≤ b₁

а₂₁х₁ + а₂₂х₂ ≤ b₂

…………..

а_m1х₁ + а_m2х₂ ≤ b_m

x₁ ≥ 0; х₂ ≥ 0.
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой а_i1х₁ + а_i2х₂ ≤ b_i i = 1, m. Условия неотрицательности определяют полуплоскости соответственно с граничными прямыми x₁ = 0; х₂ = 0.. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых составляют решение данной системы. Совокупность этих точек называют многоугольником решений. Это может быть точка, отрезок, луч, замкнутый многоугольник, неограниченная многоугольная область.⁵

Если в системе ограничений (**) - (***) n = 3, то каждое неравенство геометрически представляет полупространство трехмерного пространства, граничная плоскость которого а_i1х₁ + а_i2х₂ + а_i3х₁ ≤ b_i, а условия неотрицательности — полупространства с граничными плоскостями соответственно x_i = 0 (i = 1, 2, 3). Если система ограничений совместна, то эти полупространства, как выпуклые множества, пересекаясь, образуют в трехмерном пространстве общую часть, которая называется многогранником решений.

Пусть в системе (**) - (***) п > 3, тогда каждое неравенство определяет полупространство n-мерного пространства с граничной гиперплоскостью а_i1х₁ + а_i2х₂ + … + а_inх_n ≤ b_i i = 1, т , а условия неотрицательности — полупространства с граничными гиперплоскостями x_j = 0, j = 1, n.

Если система ограничений совместна, то по аналогии с трехмерным пространством она образует общую часть n-мерного пространства, называемую многогранником решений, так как координаты каждой его точки являются решением.

Таким образом, геометрически задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями служат все точки многогранника решений.

Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно.

Пусть задача линейного программирования задана в двумерном пространстве, т. е. ограничения содержат две переменные.

Если в ЗЛП ограничения заданы в виде неравенств с двумя переменными, она может быть решена графически. Графический метод решения ЗЛП состоит из следующих этапов.

Этап 1.

Сначала на координатной плоскости x₁Ox₂ строится допустимая многоугольная область (область допустимых решений, область определения), соответствующая ограничениям: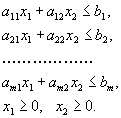
(1.6)
Не приводя строгих доказательств, укажем те случаи, которые тут могут получится.

1. 
   Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 1а).
   
2. 
   Неосновной случай  получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 1б. Подобная ситуация, например, получится, если в рассмотренном выше примере убрать ограничение х₁ + х ₂ ≤ 3. Оставшаяся часть будет неограниченным выпуклым многоугольником.
   

а)

б)

Рис. 1



Наконец, возможен случай, когда неравенства (1.6) противоречат друг другу, и допустимая область вообще пуста.

Этап 2.

В ней, кроме системы неравенств, есть еще целевая функция с₁х₁+с₂х₂ =>max.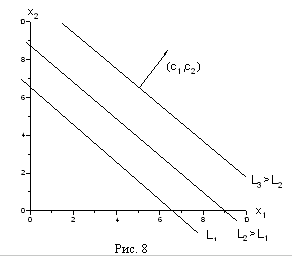

Рис. 6


Рассмотрим прямую с₁х₁+с₂х₂ = L. Будем увеличивать L. Что будет происходить с нашей прямой?

Легко догадаться, что прямая будет двигаться параллельно самой себе в том направлении, которое дается вектором (с₁,с₂), так как это  вектор нормали к нашей прямой и одновременно вектор градиента функции
f(х₁,х₂) = с₁х₁+с₂х₂ .

А теперь сведем всё вместе. Итак, надо решить задачу⁶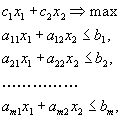



Ограничения задачи вырезают на плоскости некоторый многоугольник. Пусть при некотором L прямая с₁х₁+с₂х₂ = L пересекает допустимую область. Это пересечение дает какие-то значения переменных (х₁,х₂), которые являются планами.

Этап 3

Увеличивая L мы начнем двигать нашу прямую и её пересечение с допустимой областью будет изменяться (см. рис. 7). В конце концов эта прямая выйдет на границу допустимой области  как правило, это будет одна из вершин многоугольника. Дальнейшее увеличение L приведёт к тому, что пересечение прямой с₁х₁+с₂х₂ = L с допустимой областью будет пустым. Поэтому то положение прямой с₁х₁+с₂х₂ = L, при котором она вышла на граничную точку допустимой области, и даст решение задачи, а соответствующее значение L и будет оптимальным значением целевой функции.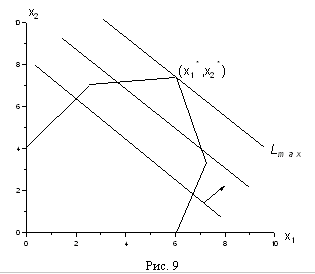


Рис. 7