Формулы для решения задач. Tкритерий Стьюдента Хi сумма всех полученных значений
 Скачать 448.86 Kb. Скачать 448.86 Kb.
|
|
t-критерий Стьюдента   Хi – сумма всех полученных значений (хi - ͞х) – сумма всех значений минус первое значение и так далее Число степеней свободы f = (n1 + n2) - 2 Сравниваем критическое и рассчитанное значения критерия: Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами. Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы. 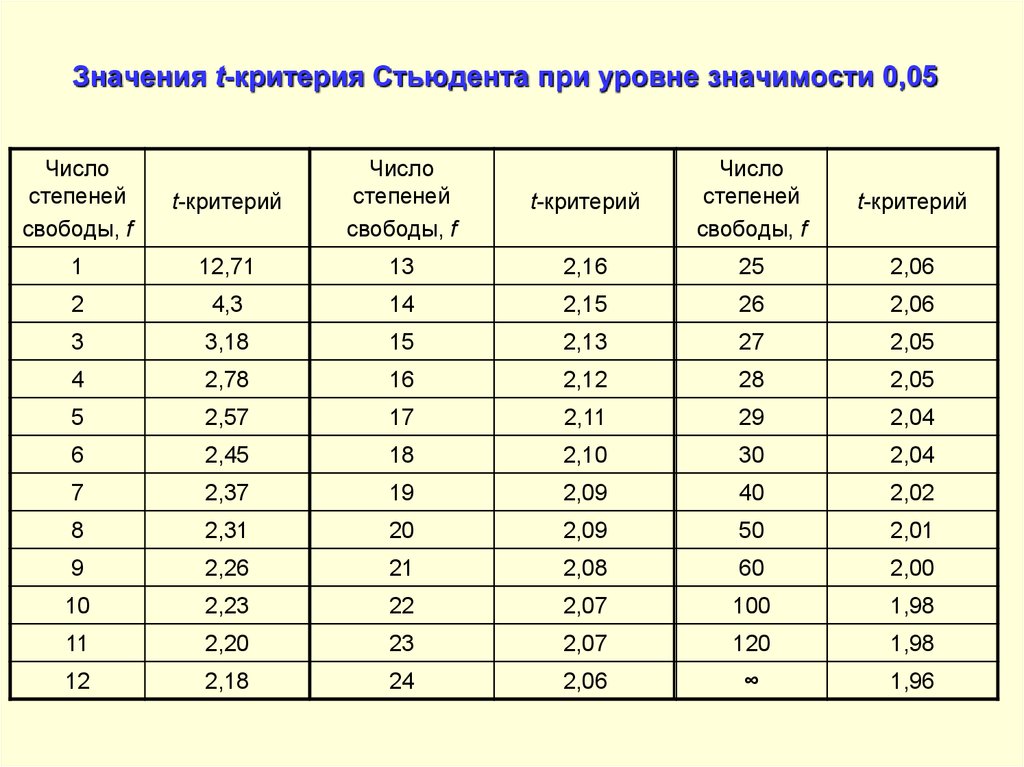 Критерий Уилкоксона T = ΣRr Как рассчитать Т-критерий Уилкоксона для связанных выборок? Вычислить разность между значениями парных измерений для каждого исследуемого. Нулевые сдвиги далее не учитываются. Определить, какие из разностей являются типичными, то есть соответствуют преобладающему по частоте направлению изменения показателя. Проранжировать разности пар по их абсолютным значениям (то есть, без учета знака), в порядке возрастания. Меньшему абсолютному значению разности приписывается меньший ранг. Рассчитать сумму рангов, соответствующих нетипичным сдвигам. Как интерпретировать значение критерия Уилкоксона? Полученное значение T-критерия Уилкоксона сравниваем с критическим по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) при заданной численности сопоставляемых выборок n: Если расчетное (эмпирическое) значение Тэмп. меньше табличного Ткр. или равно ему, то признается статистическая значимость изменений показателя в типичную сторону (принимается альтернативная гипотеза). Достоверность различий тем выше, чем меньше значение Т. Если Тэмп. больше Ткр., принимается нулевая гипотеза об отсутствии статистической значимости изменений показателя. 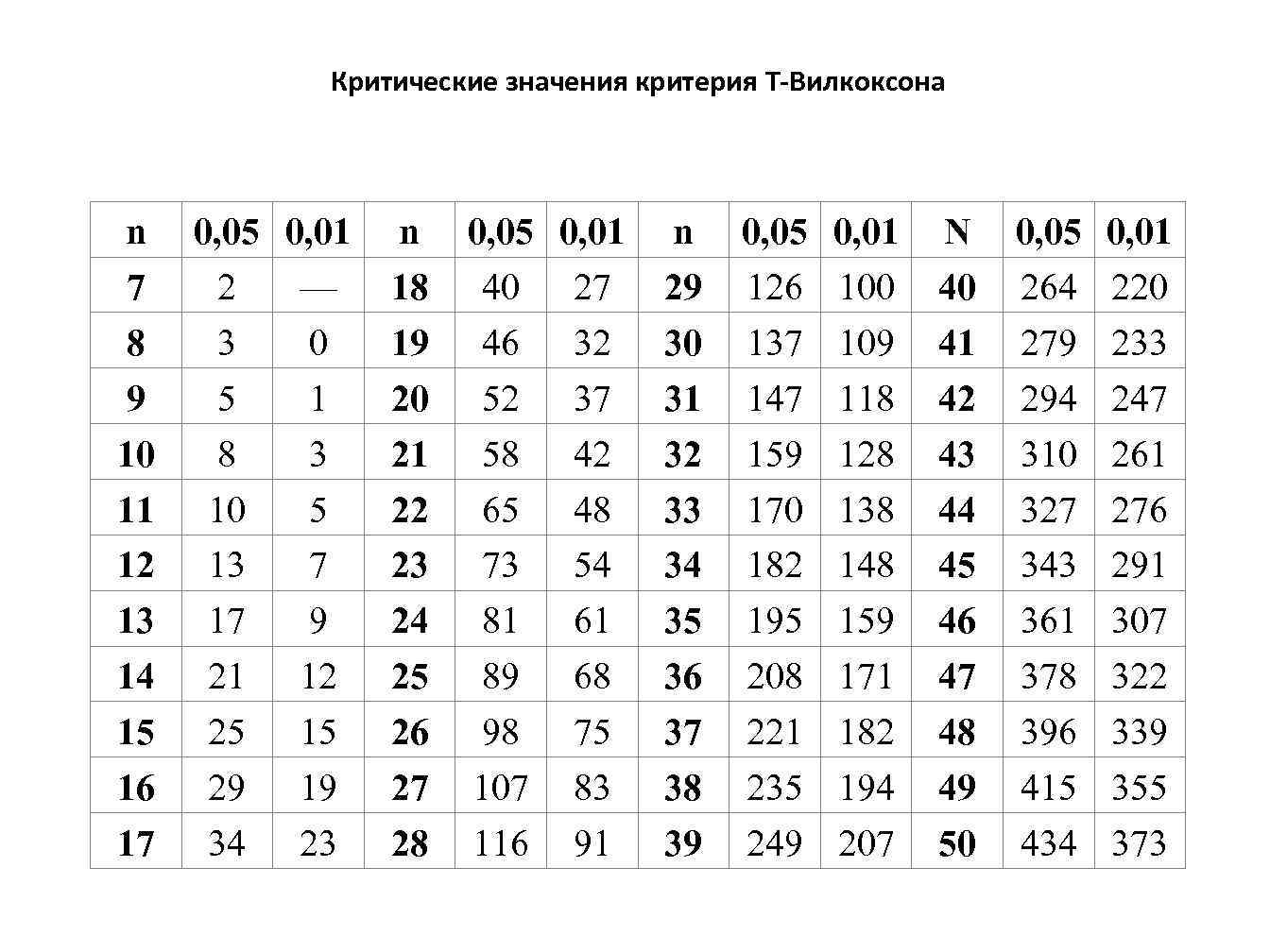 Коэффициент корреляции Пирсона Как рассчитать коэффициента корреляции Пирсона? Расчет коэффициента корреляции Пирсона производится по следующей формуле: 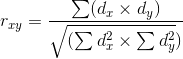 5. Как интерпретировать значение коэффициента корреляции Пирсона? Значения коэффициента корреляции Пирсона интерпретируются исходя из его абсолютных значений. Возможные значения коэффициента корреляции варьируют от 0 до ±1. Чем больше абсолютное значение rxy – тем выше теснота связи между двумя величинами. rxy = 0 говорит о полном отсутствии связи. rxy = 1 – свидетельствует о наличии абсолютной (функциональной) связи. Если значение критерия корреляции Пирсона оказалось больше 1 или меньше -1 – в расчетах допущена ошибка. Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения rxy < 0.3 свидетельствуют о слабой связи, значения rxy от 0.3 до 0.7 - о связи средней тесноты, значения rxy > 0.7 - о сильной связи. Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле: Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи. Коэффициент корреляции Спирмена Как рассчитать коэффициент Спирмена? Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию. Определить разности рангов каждой пары сопоставляемых значений (d). Возвести в квадрат каждую разность и суммировать полученные результаты. Вычислить коэффициент корреляции рангов по формуле: Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле: 5. Как интерпретировать значение коэффициента Спирмена? При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 - признаком слабой тесноты связи; значения более 0,3, но менее 0,7 - признаком умеренной тесноты связи, а значения 0,7 и более - признаком высокой тесноты связи. Также для оценки тесноты связи может использоваться шкала Чеддока:
Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи - отсутствует. Если больше, то корреляционная связь считается статистически значимой. |
