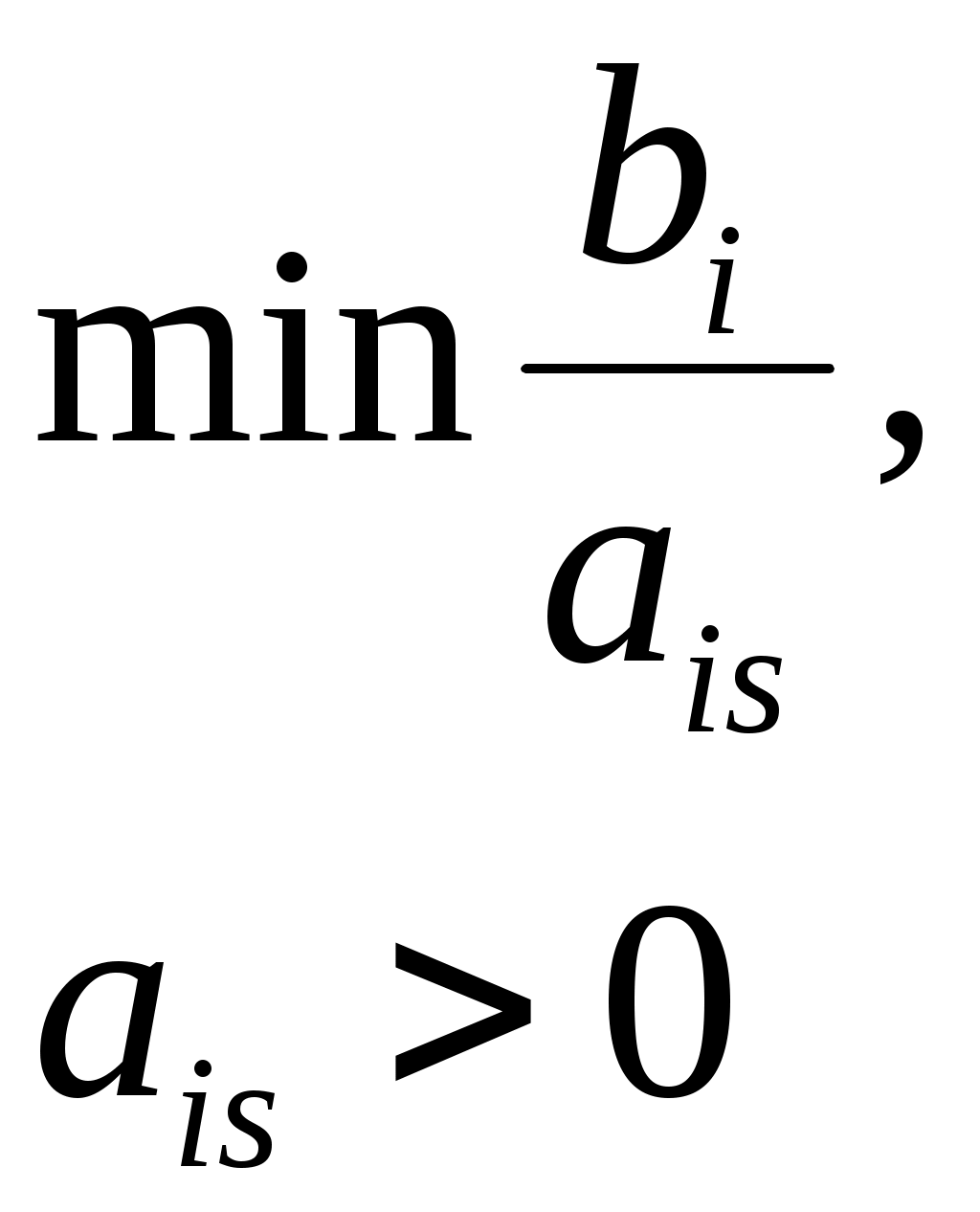Аналитический метод решения задач параметр. прогр.. Тема Аналитический метод решения задачи параметрического программирования
 Скачать 216.5 Kb.
|
Тема: Аналитический метод решениязадачи параметрического программирования.Дана линейная для каждого  целевая функция (1)и совместная система ограничений: 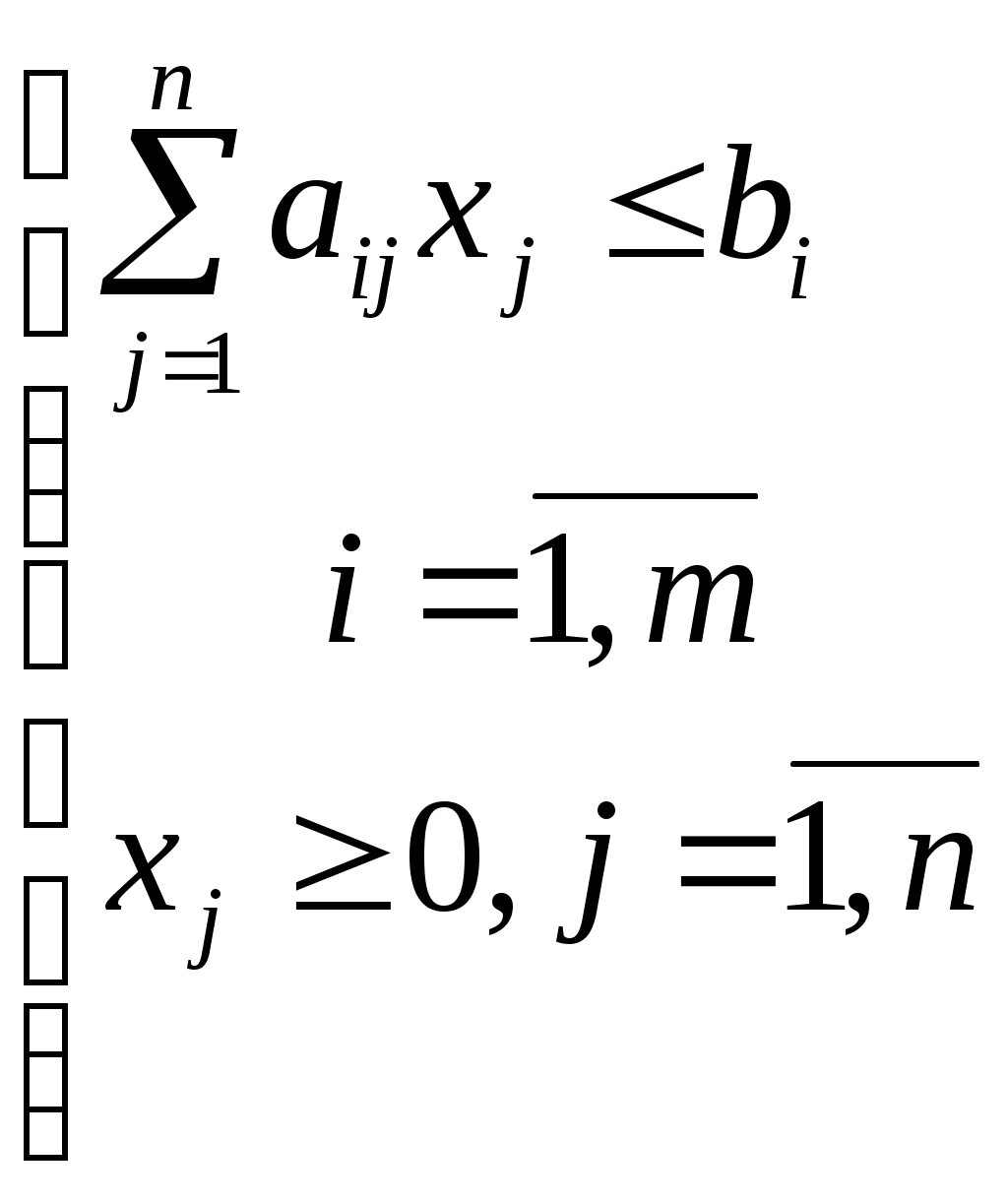 (2)Система (2) определяет непустой многогранник D. Требуется разбить отрезок  на конечное число отрезков так, чтобы для всех значений параметра максимальное значение целевой функции  достигалось в одной и той же вершине многогранника D. При этом будет линейной функцией от t на каждом из этих отрезков.Для простоты изложения будем считать, что  . Рассмотрим алгоритм решения по шагам. Первый шаг. Положим t = α и решим злп. нахождения максимума целевой функции:  при ограничениях (2). При этом к системе ограничений (2) добавим уравнение:  .Приведем задачу к стандартному виду, получим следующую модель: 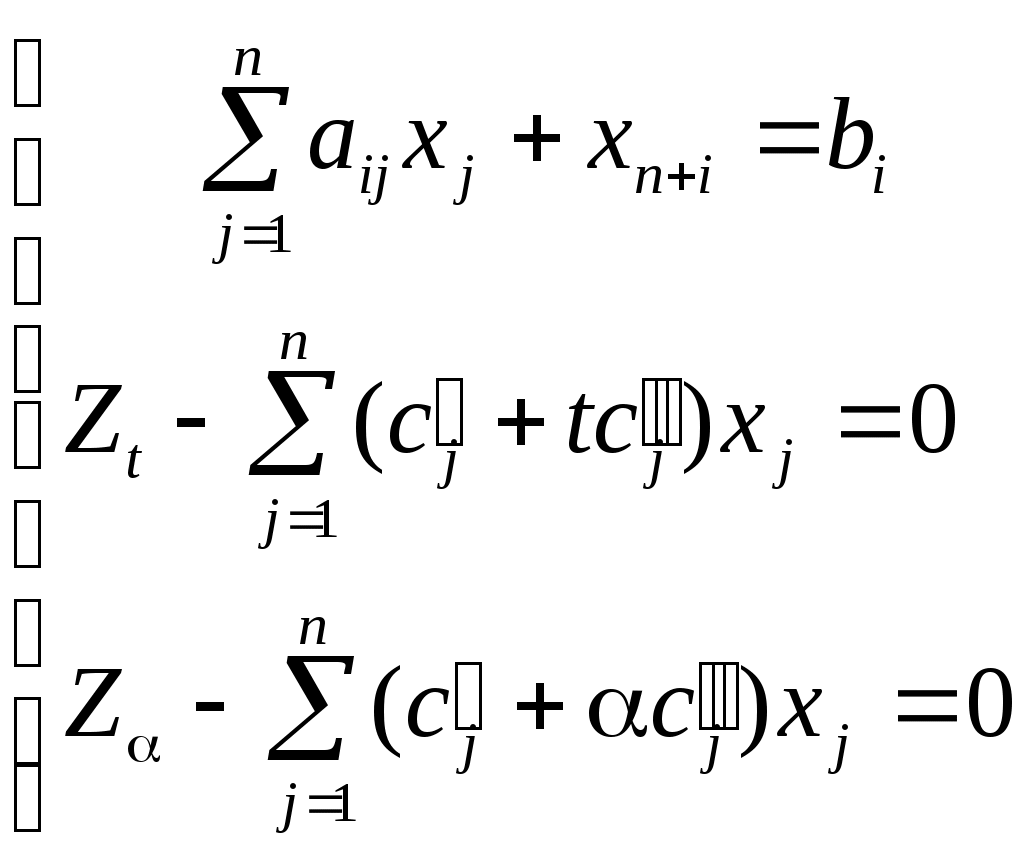 maxZα (3) (4)Исходная сокращенная симплекс таблица имеет вид:
Решив симплекс – методом задачу (3), (4) получим последующую оптимальную симплекс – таблицу.
В этой таблице все  и все оценки  ≥ 0,  ≥ 0, . . .,  ≥ 0, . . .,  ≥ 0; где:xi1, xi2 , . . ., xir, . . ., xim– базисные переменные; а xl1 ,xl2 . . ., xls , . . .,xln – свободные переменные; это переменные x1, x2, . . ., xn, xn+1, . . .,xn+m , записанные в другом порядке. Оптимальное решение задачи: 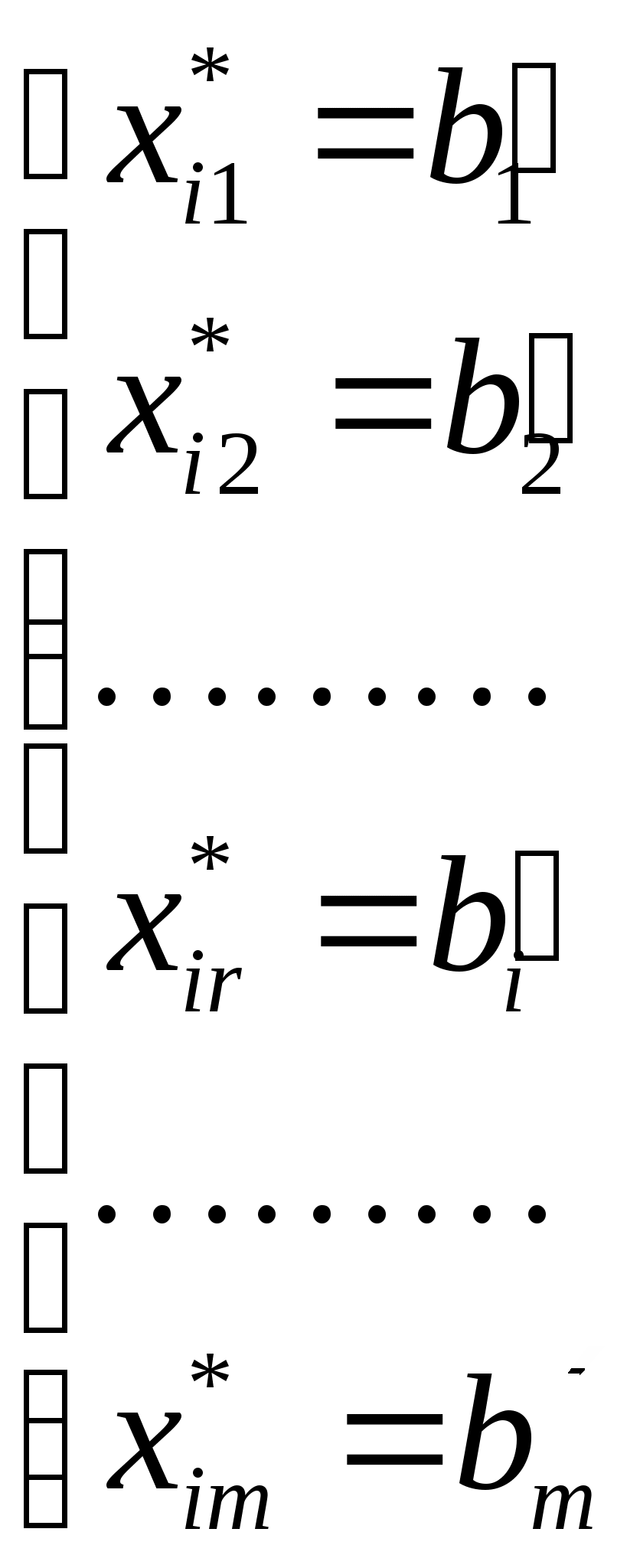 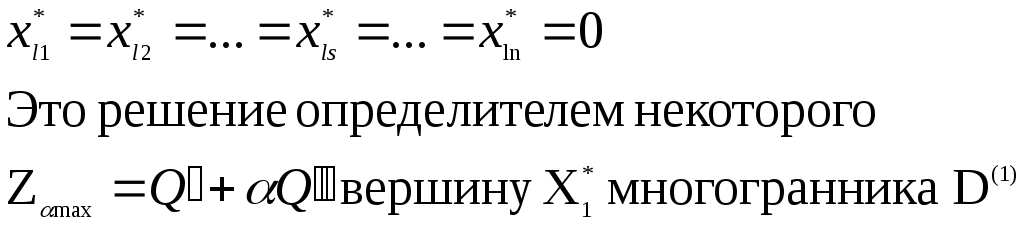 (5)Второй шаг. Надо определить все значения параметра t, при которых функция Zt достигает максимума в вершине  . Для этого найдем все те значения параметра t ,при которых оценки  ≥ 0,  , а решение (5) остается оптимальным.Решая систему линейных неравенств: 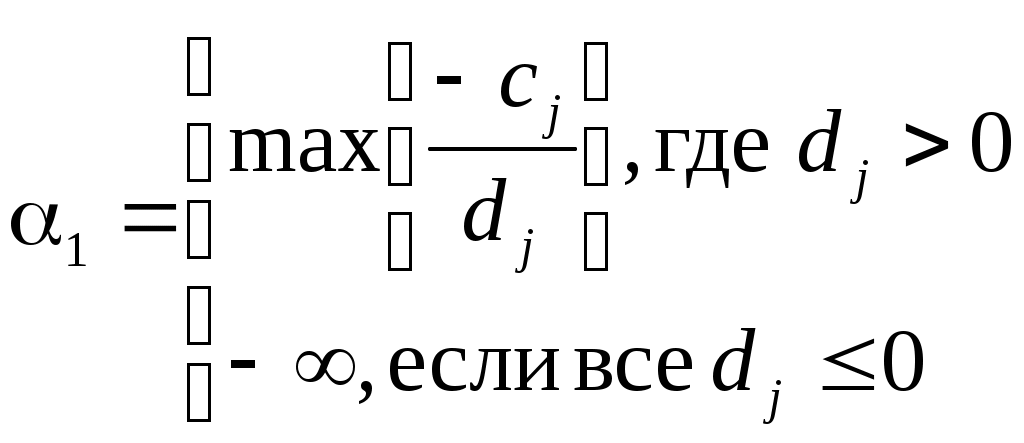≥0, . Найдем множество значений t , удовлетворяющих условиям:  , где  При этом α, может быть неотрицательной. Нас интересуют те значения t , которые принадлежат  .Если α2 ≥ β, то исходная задача решена: для всех значений t  целевая функция Zt достигает максимального значения в вершине  и  . Если α2< β переходим к третьему шагу. Третий шаг. Пусть  тогда при t > α2 коэффициент  станет отрицательным: < 0, т.к. ds > 0, т.е. в уравнении целевой функции Zt в таблице появится отрицательная оценка и вершина , т.е. решение (5) уже не будет оптимальным. Вычеркнем в таблице строку Zα. Выберем по правилам симплекс – метода в столбце s разрешающий элемент и выполним одну итерацию симплекс – метода, т.е. введем в базис переменную xs и получим новую симплекс – таблицу, из которой выписываем новое оптимальное решение при t ≥ α2 решение, соответствующее новой вершине  многогранника D. Действительно: при t = α2 оценка: =  = 0, т.е. в задаче имеется альтернативный оптимум, т.е. при t = α2 оптимальны будут две вершины и . Итак, при t ≥ α2 оптимальной будет вершина . В новой симплексной таблице для вершины проведем исследования аналогичные тем, которые провели для вершины ; т.е. переходим ко второму шагу алгоритма.Второй и третий шаги будем выполнять до тех пор, пока на втором шаге не получим значение αk ≥ β. Схематически разбиение отрезка 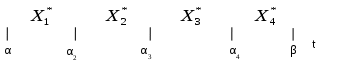можно изобразить так:  |
