Модуль 1. Тема Элементы дискретной математики Позиция 1

• Название: Тема Элементы дискретной математики Позиция 1
• Дата: 26.03.2023
• Размер: 174.48 Kb.
• Имя файла: Модуль 1.docx
• Тип: Документы; #1016335

Модуль 1. Основы теории вероятностей

Тема 1.1. Элементы дискретной математики

Позиция 1. Элементы математической логики

1. 
   Высказывание – это предложение, выражающее суждение. Высказывание должно быть повествовательным предложением. Может быть истинным или ложным.
   
2. 
   Укажите, какие конструкции русского языка и операции над множествами соответствуют логическим операциям.
   

   Операции с высказываниями	Конструкция русского языка	Операции над множествами
   Конъюнкция	и	Пересечение
   Дизъюнкция	или	Объединение
   Отрицание	не	Дополнение
   Импликация	если …, то …	Разность
   Двойная импликация	Тогда и только тогда	симметрическая разность

3. 
   Используя таблицу истинности, докажите закон де Моргана
   

1	1	0	0	1	0	0
1	0	0	1	1	0	0
0	1	1	0	1	0	0
0	0	1	1	0	1	1

4. 
   Используя таблицу истинности, докажите равенство
   

1	1	0	1	1
1	0	0	0	0
0	1	1	1	1
0	0	1	1	1

5. 
   Используя таблицу истинности, докажите равенство
   

1	1	1	1	0	0	0	1
1	0	0	0	0	1	0	0
0	1	0	0	1	0	0	0
0	0	1	0	1	1	1	1

6. 
   Как видно из заданий 3–5 настоящей позиции, все операции можно выразить при помощи отрицания и логического сложения. Зачем в логике введено такое многообразие подчиненных операций?
   

Для того, чтобы упростить запись логических высказываний.

7. 
   При помощи высказываний
   

A = {Студент получил зачет по физкультуре},

B = {Студент сдал экзамен по математике},

C = {Студент не сдал экзамен по истории}

и логических операций запишите следующие высказывания:

D₁ = {Студент сдал все дисциплины} =

D₂ = {Студент сдал ровно одну дисциплину} =

D₃ = {Студент не сдал хотя бы одну дисциплину} =

D₄ = {Если студент не сдал зачет, то он не сдаст экзамены} = .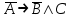

8. 
   Используя высказывания A = {Идет дождь}, B = {Стоит жара}, C = {Нужно надевать шубу}, D = {Берем зонт}, запишите литературные фразы русского языка, соответствующие следующим логическим выражениям: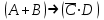
   

= «Если идет дождь или стоит жара, то нужно взять зонт и не надеть шубу».

= «Шубу нужно надевать тогда и только тогда, если нет дождя и не жарко»

= «Зонт берем тогда и только тогда, если идет дождь или если нет дождя и жарко»

9. 
   Какое значение (истина или ложь) имеет следующее высказывание: «Если слон – это насекомое, то все слоны умеют летать»?
   

Обоснуйте ответ.

Ответ: ИСТИНА. Так как высказывание: = «слон – это насекомое» является ложным, то импликация является истиной не зависимо от того, каким будет высказывание .
Позиция 2. Основные понятия комбинаторики

1. 
   A = {Выпало 5 очков при бросании игральной кости}
   

B = {Выпало 5 очков при бросании двух игральных костей}

Описывают ли приведенные высказывания исход действия, или они являются составными событиями?

Высказывание А описывает исход действия так как является неделимым результатом действия; высказывание В является составными событием так как его можно разделить на два исхода, например {Выпало 2 очка на первой игральной кости} и {Выпало 3 очка на второй игральной кости}.

2. 
   Из мешка, содержащего шары белого и красного цвета, достают один шар. Имеется высказывание A = {вынутый шар белого цвета}. В каком случае приведенное высказывание описывает исход действия? Обоснуйте ответ.
   

Приведенное высказывание описывает исход действия в случае, если в мешке находился единственный шар белого цвета. Если их больше, то приведенное высказывание является составными событием так как его можно разделить на несколько исходов.

3. 
   Дайте определения совместных и несовместных событий. Проиллюстрируйте определения на кругах Эйлера.
   

События А и В называются совместными, если существуют исходы, при которых истинными являются оба события А и В. То есть, если пересечение А и В – не пустое множество.

События называются несовместными, если не существует исходов, при которых истинными являются оба события А и В. То есть, если пересечение А и В – пустое множество.

Круги Эйлера – см. рисунок.
Позиция 3. Комбинаторный принцип сложения и его следствия

1. 
   В списке отличников 16 студентов, а в списке спортсменов 22 студента. Что мешает дать однозначный ответ на вопрос: «Сколько студентов будет в объединенном списке?»?
   

Мешает отсутствие информации о том, сколько имеется отличников-спортсменов, которые, очевидно, входят в оба списка – и отличников, и спортсменов.

2. 
   На первом курсе 45 студентов, из которых на хорошо и отлично сдали математику 22 студента, экономику – 32, историю – 36, математику и экономику – 13, математику и историю – 15, все три дисциплины – 5. Сколько студентов на хорошо и отлично сдали экономику и историю?
   

Ответ легко получить с помощью кругов Эйлера.

Получаем: все три дисциплины на хорошо и отлично сдали 5 студентов, а математику и экономику – 13. То есть, математику и экономику на хорошо и отлично, а историю – хуже, сдало 13-5=8 студентов. Аналогично, математику и историю на хорошо и отлично, а экономику – хуже, сдало 15-5=10 студентов.

Таким образом, имеем ОШИБКУ В УСЛОВИИ: математику на хорошо и отлично сдало не меньше 5+8+10=23 студентов.

Обозначим количество студентов, которые сдали экономику и историю на хорошо и отлично, а математику – хуже, через х. Тогда получим систему из 2 уравнений:

Экономика: 32–(5+8+х) = количеству студентов, которые сдали экономику на хорошо и отлично, а математику и историю – хуже.

История: 36–(5+10+х) = количеству студентов, которые сдали историю на хорошо и отлично, а математику и экономику – хуже.

Последние числа неизвестны. Поэтому, похоже, УСЛОВИЕ НЕ ПОЛНОЕ: не хватает информации. Например, сколько студентов из 45 сдали хотя бы один предмет на хорошо и отлично.

3. 
   Компьютерное тестирование прошли 72 студента. Треть студентов дали от 50% д 59 % правильных ответов, четверть студентов дали от 60 % до 75 % правильных ответов, а более 75% правильных ответов дали 10 студентов. Сколько студентов дали меньше 60% правильных ответов?
   

От 60 % до 75 % правильных ответов дало четверть студентов, т.е. 72/4=18 студентов, а более 75% правильных ответов дали 10 студентов.

Тогда 60 и больше % правильных ответов дало 18+10=28 студентов.

Значит меньше 60% правильных ответов дало 72-28=44 студента.
Позиция 4. Комбинаторный принцип умножения

1. 
   Студент Рома рассуждает: «В одном списке 10 отличников, а в другом – 15 спортсменов. Значит, согласно принципу умножения количество студентов, которые являются ОТЛИЧНИКАМИ И СПОРТСМЕНАМИ одновременно, 10*15 = 150 человек!». Найдите ошибку в рассуждениях студента.
   
2. 
   Студент Рома, отправляясь на экзамен, рассовывает пять различных шпаргалок по четырем карманам. Какое количество способов рассовывания возможно?
   

Каждую шпаргалку можно расположить 4 способами (в один из четырех карманов). То есть всего способов 4*4*4*4*4=4⁵=1024 способа.

3. 
   Как изменится решение предыдущей задачи, если в нагрудном кармане должна оказаться ровно одна шпаргалка?
   

Тогда сначала выберем одну из 5 шпаргалок в нагрудный карман – 5 способов, а потом получаем аналогично для 4 шпаргалок и 3 карманов количество способов 3⁴=81. Всего способов 5*3⁴=5*81=405 способов.
Позиция 5. Перестановки и размещения

1. 
   Приведите подробные рассуждения, дающие вывод формулы числа перестановок, на примере: Для премирования пяти работников директор взял по одной купюре достоинства 50, 100, 500, 1000 и 5000 рублей и разложил их в пять одинаковых конвертов. Какое количество вариантов премирования может получиться, если в каждом конверте ровно одна купюра?
   

Для премирования первого работника существует 5 вариантов премии – любая купюра из 50, 100, 500, 1000 или 5000 рублей. После премирования первого работника, независимо от премии первого работника, для премирования второго работника остается 4 варианта премии – любая купюра из 50, 100, 500, 1000 или 5000 рублей, кроме той, что пошла на премию первого работника; для премирования третьего работника остается 3 варианта премии и т.д. Таким образом, вариантов премирования может получиться 5*4*3*2*1=5!=120 вариантов.

2. 
   Во сколько раз изменится ответ в примере на стр. 15, если изменить вопрос задачи: «Сколько вариантов того, что из вынутых букв можно сложить имя студента?»?
   

Ответ увеличится в P₄ = 4! = 4*3*2*1 = 24 раз – количество перестановок из 4 букв.

3. 
   Одиннадцать друзей студента Ромы на его дне рождения стали водить хоровод вокруг именинника и пить водку: «Каравай, каравай…». Каким числом способов можно образовать такой хоровод?
   

Так как друзья Ромы ходили по кругу, то можно считать, что место одного из друзей (например, лучшего друга Ромы) фиксированным, поэтому число способов, которым можно образовать такой хоровод равно числу перестановок из 10 элементов, т.е. P₁₀ = 10! = 10*9*8*7*6*5*4*3*2*1 = 3628800 способов.
ДАЛЕЕ – ТОЛЬКО РЕШЕНИЕ, БЕЗ УСЛОВИЯ!

4. 
   Тогда следует воспользоваться формулой
   
5. 
   Потому что число шпаргалок в задаче 2 (стр.15) больше, чем число карманов, поэтому выборка не являлась бесповторной.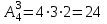
   
6. 
   вариантов.
   
7. 
   Тогда число способов инвестиций будет равно (3 депозита и 3 возможных бизнес-проекта) вариантов, т.е. уменьшится в 4 раза.
   

! Либо неполное условие -
Позиция 6. Число сочетаний и его свойства.

1. 
   Для выбора первого работника для премирования существует 8 способов; для выбора второго работника для премирования существует 8–1 = 7 способов; … для выбора пятого работника для премирования существует 8–4 = 4 способа. Но, поскольку все премии одинаковы, то в полученном число способов учтены как разные такие варианты распределения премий, при которых премии получат одни и те же рабочие, но в разном порядке (например ABCDE и ABCED и т.д.) Поэтому полученное число способов следует разделить на число перестановок из 5 рабочих – 5! Получаем _. Умножив теперь на 3! числитель и знаменатель, получим формулу
   
2. 
   См. рисунок.
   

Свойство симметричности числа сочетаний проявляется в виде симметрии строк треугольника Паскаля.

3. 
   Число вариантов равно количеству вариантов распределения в первую десятку 4 экономистов из 7 возможных и 6 юристов/психологов из 11 возможных:
   

4. 
   Из общего числа вариантов распределения 18 человек в первую десятку, т.е. следует отнять число вариантов, при каких в первую десятку войдет меньше 2 (то есть 0 или 1) экономистов:
   

Позиция 7. Классическое определение вероятности

1. 
   Полные группы событий:
   

• 
  бросают две монеты: А₁=(выпало 2 герба); А₂=(выпал 1 герба и 1 решка) А₃=(выпало 2 решки)
  
• 
  студент сдает за сессию три экзамена: А₁=(сдал 3 экзамена); А₂=(сдал 2 экзамена и 1 не сдал); А₃=(сдал 1 экзамен и 2 не сдал); А₄=(не сдал 3 экзамена).
  

2. 
   События не являются простейшим, т.к. их можно разложить на более простые. Например, событие А₂ можно разложить на такие: (на первой монете выпал герб, а на второй монете выпала решка) и (на первой монете выпала решка, а на второй монете выпал герб)
   
3. 
   Ω = (выбирают 4 вопроса из 25 возможных)
   

N = N(Ω) =

A= (Роме в билете попалось 2 вопроса из 15 выученных и 2 из 10 невыученных)

_M=N(A)=

4. 
   Р(случайно выбранный шарик надул Рома)
   

Р(из двух случайно выбранных шариков Маруся надула оба)

Р(из шести случайно выбранных шариков Маруся надула не менее трех) =

5. 
   Событие А = (слово не изменилось) произойдет, если на первом месте стоит одна из 2 имеющихся в слове КОЛОКОЛ букв «К», на втором – одна из 3 имеющихся в слове КОЛОКОЛ букв «О», на втором – одна из 3 имеющихся в слове КОЛОКОЛ букв «О», на третьем – одна из 2 имеющихся в слове КОЛОКОЛ букв «Л», на четвертом – одна из 2 оставшихся букв «О», на пятом – одна из 1 оставшихся букв «К», на шестом – одна из 1 оставшихся букв «О», на седьмом – одна из 1 оставшихся букв «Л». То есть N(A) = 2!*3!*2!
   

Всего из 7 букв можно составить 7! комбинаций. Поэтому

Р(слово не изменилось)

6. 
   Недостатки классического определения вероятности :
   

число элементарных исходов часто очень велико и даже бесконечно;

в прикладных задачах трудно указать основания, позволяющие считать элементарные события равновозможными;

только в редких случаях уже перед началом наблюдения можно вычислить все равновозможные несовместные события и в том числе благоприятные события.

Позиция 8. Вероятность суммы событий

1. 
   Обозначим А = (студент первого курса сдал математику); В = (студент первого курса сдал историю). Тогда Р(А)=5/9; Р(В)=3/4; Р(А+В)=6/7.
   

По формуле вероятности суммы событий



Откуда выражаем

2. 
   Ответ: эти события не могут быть несовместимыми, так как тогда бы
   

что невозможно, так как вероятность не больше 1.

3. 
   Воспользуемся формулой обратной вероятности
   

Тут событие



Отметим, что события А0 , А1 являются несовместимыми, поэтому








Позиция 9. Вероятность произведения событий

1. 
   Условная вероятность – вероятность одного события при условии, что другое событие уже произошло.
   
2. 
   Обозначим события А = (Маруся неправильно прочла вопрос); В = (Маруся допустила арифметическую ошибку). Тогда из условия задачи имеем такую информацию: Р(А) = 0,16; Р(В) = 0,11; Р(А+В) = 1–0,78 = 0,22.
   

Отсюда несложно вычислить



Теперь воспользуемся свойством условных вероятностей

3. 
   Обозначим события А₁ = (Маруся передала Роме шпаргалку по математике); А₂ = (Маруся передала Роме шпаргалку по философии). Тогда из условия задачи имеем такую информацию: Р(А₁) = 5/8; Р(А₂) = 3/8.
   

Тогда по формуле полной вероятности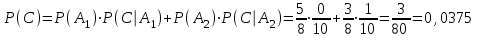

4. 
   Вероятные независимые события не могут быть несовместными, так как тогда бы вероятность их произведения, с одной стороны равнялась бы 0 (в силу несовместимости), а, с другой стороны, равнялась бы ненулевому (в силу того, что события вероятны) произведению вероятностей этих событий (в силу независимости).
   
5. 
   Обозначим события А₁ = (прибыль принесет первый вклад); А₂ = (прибыль принесет второй вклад); А₃ = (прибыль принесет третий вклад). Тогда из условия задачи имеем: А₁, А₂, А₃ –независимы; Р(А₁) = 0,4; Р(А₂) = 0,7; Р(А₃) = 0,8.
   

Поэтому





=0,4*0,7*(1–0,8)+ 0,4*(1–0,7)*0,8+(1–0,4)*0,7*0,8=0,488

6. 
   Обозначим события А₁ = (первая шпаргалка, которую достала Маруся, – по математике); А₂ = (вторая шпаргалка, которую достала Маруся, – по математике); А₃ = (третья шпаргалка, которую достала Маруся, – по математике). Тогда из условия задачи: события А₁, А₂, А₃ – зависимы; причем исходя из классического определения вероятности Р(А₁) = 5/8; Р(А₂| А₁) = 4/7; Р(А₃| А₁А₂) = 3/6.
   

Теперь используем формулу

7. 
   Тогда события А₁, А₂, А₃ – независимы; причем исходя из классического определения вероятности Р(А₁) = Р(А₂) = Р(А₃) = 5/8.
   

8. 
   Различие в решениях двух предыдущих задач связано с зависимостью либо независимостью событий А₁, А₂, А₃.
   

Позиция 10. Формула полной вероятности и формула Байеса.

1. 
   Формула полной вероятности :
   

Формула Байеса:

2. 
   Р(Н₁)=5/20 Р(Н₂)=7/20 Р(Н₃)=8/20
   

Р(А|Н₁) = 1 Р(А|Н₁) = 0,6 Р(А|Н₁) = 0,1

Р(А) = 5/20*1 + 7/20*0,6 + 8/20*0,1 = 0,25 + 0,21 + 0,04 = 0,5

3. 
   Будем использовать формулу Байеса.
   

на полностью выученный вопрос: 5/20*1 : 0,5 = 0,25/0,5 = 0,5;

на частично выученный вопрос: 7/20*0,6 : 0,5 = 0,21/0,5 = 0,42;

на плохо выученный вопрос: 8/20*0,1 : 0,5 = 0,04/0,5 = 0,08.

4. 
   Будем использовать формулу Байеса. Искомая вероятность равна
   

Позиция 11. Определение случайной величины.

1. 
   Х₁ – количество заданных Роме вопросов
   

Х₂ – количество вопросов, на которыеРома ответил правильно

Х₃ – количество вопросов, на которыеРома ответил неправильно

2. 
   А = (стрелок попал хотя бы раз);
   

Х(В) = {0; 2; 4}.

3. 
   Примером случайного процесса, которому соответствует случайная величина, принимающая все натуральные значения может быть, например, срок службы (в секундах) электролампочки.
   

Позиция 12. Дискретные случайные величины (ДСВ)

1. 
   а) p_k > 0 – смысл в том, что все события (X = x_k) являются возможными
   

б) p₁+…+p_n = 1 – смысл в том, что указаны все возможные события (X = x_k) и их вероятности.

2. 
   p₁ = Р(Х = 0) = Р(нет правильно заполненных отчетов) = 0,4*0,3 = 0,12
   

p₂ = Р(Х = 1) = Р(1 отчет правильно заполнен) = 0,4*(1–0,3)+(1–0,4)*0,3 = 0,46

p₃ = Р(Х = 2) = Р(2 отчета правильно заполнены) = (1–0,4)*(1–0,3) = 0,42

Проверка правильности вычислений:p₁+ p₂ + p₃ = 0,12+0,46+0,42 = 1. Верно.

Запишем закон распределения дискретной случайной величины Х:

xk	0	1	2
P(X = xk)	0,12	0,46	0,42

Позиция 13. Операции с дискретными случайными величинами

1. 
   Функциональная связь между ДСВ X и Y : Y = 150(2 – X)
   

Закон распределения дискретной случайной величины Y:

yk	0	150	300
P(Y = yk)	0,42	0,46	0,12

2. 
   Закон распределения дискретной случайной величины Z₁:
   

zk	0	200
P(Z = z1k)	0,4	0,6

Закон распределения дискретной случайной величины Z₂:

zk	0	100
P(Z = z2k)	0,3	0,7

Закон распределения дискретной случайной величины Z = Z₁ +Z₂:

Z1 \ Z2	0	100
0	0,12	0,28
200	0,18	0,42

Таким образом, закон распределения дискретной случайной величины Z :

zk	0	100	200	300
P(Z = zk)	0,12	0,28	0,18	0,42

Позиция 14. Геометрическое определение вероятностей

1. 
   ––––––––
   
2. 
   Является. Классическое определение вероятности можно трактовать как количество точек, попавших в некоторый интервал или геометрическую фигуру.
   
3. 
   Например, подобной мерой множества может быть несобственный интеграл.
   

Позиция 15. Функция распределения и ее свойства

1. 
   Для приведенного графика функции F(x)
   
2. 
   F(x) неубывающая функция – не выполнено
   

F(x) ≥ 0 – выполнено

F(x) ≤ 1 – не выполнено

– не выполнено

– выполнено

F(x) полунепрерывная слева функция – не выполнено (в точке a)

3. 
   Следствие 1: P(X ≥ b) = 1 – F(b)
   

Следствие 2: P(a ≤ X < b) = F(b) – F(a)

Следствие 3: P(X = a) = F(a+0) – F(a)

4. 
   P(X < 3) = F(3) = 5/6
   

P(X = 4) = 0

P(X = 1) = 3/4–4^–1 = 3/4 – 1/4 = 1/2

P(X ≥ 1) = 1 – 4^–1 = 1 – 1/4 = 3/4

P(–2 ≤ X < 1) = 4^–1 – 4^–4 = 1/4 – 1/64 = 15/64

P(1 < X < 5) = 7/8 – 3/4 = 1/8

Позиция 16. Непрерывные случайные величины

1. 
   
   

а) f(x) ≥ 0 – так как функция распределения – неубывающая функция, то ее производная (т.е. плотность) – неотрицательна.

б) – так как и

2. 
   См. рисунок.
   
3. 
   Для нахождения плотности f_Y(t) сначала найдем функцию распределения F_Y(t), а потом продифференцируем ее. Итак,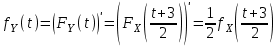
   

Позиция 17. Численные характеристики ДСВ

1. 
   Дисперсия это DX = M(X – MX)²
   

Свойства DX: DC = 0

D(αX) = α²DX

D(X ± Y) = DX ± DY

Mo(X) – Мода ДСВ это такое значение ДСВ x_k , которое имеет наибольшую вероятность p_k

2. 
   
   

   xk	–1	1	2	4	7	Σ
   pk	0,3	0,4	0,15	0,05	0,1	1→ X–ДСВ
   xkpk	–0,3	0,4	0,3	0,2	0,7	a = MX = 1,3
   x2kpk	0,3	0,4	0,6	0,8	4,9	MX2 = 7
   (xk–a)2	5,29	0,09	0,49	7,29	32,49	*******
   (xk–a)2pk	1,587	0,036	0,0735	0,3645	3,249	DX = 5,31

3. 
   Воспользуемся свойствами математического ожидания:
   

DX = M(X – MX)² = M(X² – 2XMX+ (MX)²) = M(X²) – M(2XMX)+ M(MX)² ==M(X²) – 2M(X)M(X)+ (MX)² =M(X²) – 2(MX)² + (MX)² = M(X²) – (MX)²

Тогда для примера 2 ранее : DX = 7 – (1,3)2 = 7 –1,69 = 5,31

4. 
   Одно из значений, как следует из определения моды, 7. Далее, вероятность, соответствующая этому значению, равна большему из чисел 0,4 и 1–0,4=0,6. Т.е. 0,6. Второе возможное значение ДСВ Х найдем из определения математического ожидания:
   

MX = 5 = x₁p₁ + x₂p₂ = x₁*0,4 + 7*0,6

0,4x₁ = 0,8 то есть x₁ = 2

Ответ: ДСВ Х принимает значения 2 и 7.

5. 
   Обозначим вероятности соответственно p₁ и p₂ . Тогда
   

MX = x₁p₁ + x₂p₂ = 2*p₁ + 5*p₂ ≤ 3.

С другой стороныp₁ + p₂ = 1, значит p₁= 1– p₂. Подставим в формулу для МХ:

2*(1– p₂)+ 5*p₂ ≤ 3

3p₂ + 2 ≤ 3

p₂ ≤ 1/3

Тогда p₁ ≥ 1– 1/3 = 2/3.

Соответственно, Mo(X) = 2.

6. 
   Для доказательства найдем MY и DY и покажем, что MY = 0 а DY = 1.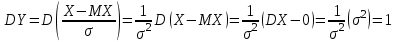
   

Позиция 18. Численные характеристики НСВ

1. 
   
   

Mo(X) – мода НСВ – это точка максимума плотности распределения НСВ Х

2. 
   -----------------
   
3. 
   Квантиль уровня α – это такое число, что данная случайная величина попадает левее его с вероятностью, равной α: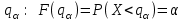
   

На графике функции распределения квантиль уровня α – это такое значение х, при котором функция распределения равна α; на графике плотности распределения квантиль уровня α – это такое значение qα, что площадь фигуры, ограниченной сверху графиком плотности, снизу осью Oy и справа прямой x = qα, равна α .

+ См. рисунок.

Критическое значение уровня γ – это такое число, что данная случайная величина попадает правее его с вероятностью, равной γ:



На графике функции распределения критическое значение уровня γ – это такое значение х, при котором функция распределения равна 1 – γ; на графике плотности распределения критическое значение уровня γ – это такое значение Rγ, что площадь фигуры, ограниченной сверху графиком плотности, снизу осью Oy и слева прямой x = Rγ, равна γ .

+ См. рисунок.

4. 
   Медиана НСВ – это квантиль уровня 0,5, т.е.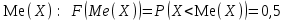
   

5. 
   См. рисунок.
   

Позиция 19. Закон больших чисел (ЗБЧ)

1. 
   Неравенство Маркова:
   

Неравенство Чебышева:

2. 
   Из условия получим, что X – «количество вопросов, на которые Рома ответил правильно» – неотрицательная случайная величина; MX = 0,35*20 = 7.
   

При помощи неравенства Маркова:



При помощи неравенства Чебышева:

3. 
   Правило «трех сигм»: вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
   

Объяснение при помощи неравенства Чебышева:

4. 
   ЗБЧ для случая одинаково распределенных СВ.
   

Пусть СВ X_i – независимы, одинаково распределены с MX_i = a . Тогда



_{Практическое применение данной теоремы – например, выборочный метод в математической статистике, когда по сравнительно небольшой выборке судят о всей совокупности.}

Словарь терминов по модулю 1

Случайное событие – это событие, которое может произойти или не произойти при осуществлении совокупности условий, связанных с возможностью появления данного события.

Сумма событий А и В – это событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Произведение событий А и В – это событие АВ, которое наступает тогда и только тогда, когда наступают оба события А и В одновременно.

Независимые события: события событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого.

Повторный/бесповторный выбор: при повторном выборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку, а при бесповторном выборе не возвращается.

Процесс с неполной информацией – это процесс, для которого отсутствует вся информация о его поведении в прошлом; известно лишь его значение в настоящий момент времени T.

Нормированная СВ – это случайная величина Y, связанная с исходной СВ X линейным преобразованием

Закон больших чисел (в широком смысле, по А.Н. Колмогорову) – совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Закон больших чисел (в узком смысле) – ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.