тепло. Тема Функции. Область определения и множество значений график функции, построение графиков функции, заданных различными способами. Свойства функции. Цель

• Название: Тема Функции. Область определения и множество значений график функции, построение графиков функции, заданных различными способами. Свойства функции. Цель
• Анкор: тепло
• Дата: 06.03.2022
• Размер: 136 Kb.
• Имя файла: 80_funktsii_oblast_opredeleniya_i_mnozhestvo_znacheniy (2).doc
• Тип: Документы; #384929

Тема: Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.

Цель:

• 
  дать определение понятий «функция», «область определения», «область значений», «график функции»;
  
• 
  рассмотреть способы задания функций;
  
• 
  рассмотреть свойства функций (нули функций, промежутки знакопостоянства, промежутки возрастания и убывания функции, четность и нечетность функции)
  
• 
  рассмотреть свойства некоторых элементарных функций
  

Теоретическая часть

Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.

Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.

Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y=f(x). (Читают: у равно f от х.) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х.

Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.

Способы задания функции:

1.      аналитический способ (функция задается с помощью математической формулы;

2.      табличный способ (функция задается с помощью таблицы)

3.      описательный способ (функция задается словесным описанием)

4.      графический способ (функция задается с помощью графика).

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

 

ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ

1.Нули функции

Нуль функции – такое значение аргумента, при котором значение функции равно нулю .

2.Промежутки знакопостоянства функции

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

            3. Возрастание (убывание) функции.

Возрастающая в некотором промежутке функция - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Функция у = f(x) называется возрастающей на интервале (а; b), если для любых x₁и x₂из этого интерва­ла таких, что x₁< x₂ , справедливо неравенство f(x₁)<f(x₂).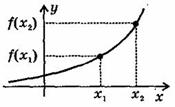



Убывающая в некотором промежутке функция - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Функция у =f(x) называется убывающей на интервале (а; b), если для любых  x₁и x₂из этого интервала таких, чтоx₁< x₂,справедливо неравенство f(x₁)>f(x₂).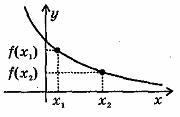



 

 

4. Четность (нечетность) функции

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Например, у = х² -  четная функция.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

Например: у = х³ - нечетная функция.

Функция общего вида не является четной или нечетной (у = х²+х).

 

Свойства некоторых функций и их графики

 

1.      Линейной функцией называется функция вида , где  kи b– числа.

Область определения линейной функции – множество R действительных чисел.

Графиком линейной функции у = kx + b (k ≠ 0) является прямая проходящая через точку (0; b) и параллельная прямой у = kx.

Прямая, не параллельная оси Оу, является графиком линейной функции.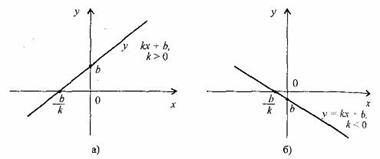



Свойства линейной функции.

1. При k > 0 функция у = kx + bвозрастающая в области определения.

2. При k < 0 функция у = kx + bубывающая в области определения.

3.  Множеством значений функции y = kx + b(k ≠ 0) является вся числовая прямая, т.е. множество Rдействительных чисел.

При k = 0 множество значений функции у = kx + bсостоит из од­ного числа b.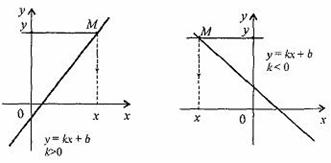

 



3.      При b = 0 и k= 0 функция не является ни четной, ни нечетной.

При k = 0 линейная функция имеет вид  у = bи при b ≠ 0она является четной.

При k= 0 и b = 0 линейная функция имеет вид у = 0 и являете одновременно четной и нечетной.

Графиком линейной функции  у = bявляется прямая, проходящая через точку (0;b)и параллельная оси Ох. Заметим, что при b= 0 график функции у = bсовпадаете осью Ох.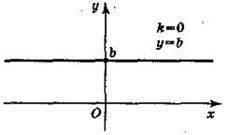



5. При k > 0 имеем, что у > 0, если и у < 0, если  . При k < 0 имеем, что у > 0, если  и у < 0, если .

2. Функция y = x²

Область определения этой функции - множество R действительных чисел.

Придавая переменной х несколько значений из области опреде­ления функции и вычисляя соответствующие значения у по формуле y = x², изображаем график функции.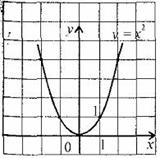

 



График функции y = x² называется параболой.

Свойства функции у = х².

1.  Если х = 0, то у = 0, т.е. парабола имеет с осями координат общую точку (0; 0) - начало координат.

2.  Если х ≠ 0, то у > 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.

3.   Множеством  значений  функции у = х²является промежуток [0; + ∞).

4.  Если значения аргумента отличают­ся только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = х² - четная).

5.  На промежутке [0; + ∞) функция у = х²возрастает.

6.  На промежутке (-∞; 0] функция у = х²убывает.

7.  Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.

 

3.Фунуция

Область определения этой функции - промежуток  [0;+∞), т. е. все неотрицательные числа.

Придавая переменной х несколько значений из области определения функции и вычисляя соответст­вующие значения у по формуле 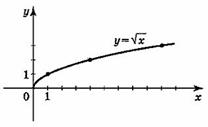, изображаем график функции.

 



Свойства функции.

1.  Если х = 0, то у = 0, т.е. график функции имеет с осями координат общую точку (0; 0) - начало координат.

2.  Если х > 0, то у > 0, т.е. все точки графика функции, кроме начала координат, лежат над осью абсцисс.

3.  Множеством значений функции является промежуток [0;+∞).

4. Функция не является ни четной, ни нечетной.

5. Функция возрастающая в области определения.

6.  Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.

 

4. Функция y = x³

Область определения этой функции - множество R действительных чисел,

Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле у = х³, изображаем график функции.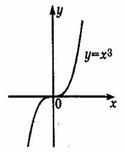



График функции у= х³называется кубической параболой.

Свойства функции y = x³.

1.  Если х = 0, то у = 0, т.е. кубическая парабола пересекает оси координат в точке (0; 0) - начале координат.

2.  Если х > 0, то у > 0, а если х < 0, то у < 0, т.е. кубическая парабола лежит в первом и третьем координатном углах.

3.  Множеством значений функции у =  х³является вся числовая прямая.

4.   Если значения аргумента отличаются только знаком, то и значения функции отличаются  только  знаком, т.е.   кубическая парабола симметрична относительно начала координат (функция у =  х³ - нечетная).

4.      Функция у = х³возрастающая в области определения.

 

5.Функция y = |x|

Область определения этой функции - множество R  действительных чисел.

Пользуясь определением модуля числа х при х > О получим у = х, а при х <0 получим у = - х. Таким образом, имеем: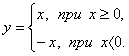



График функции состоит из двух частей: части прямой у = х при х ≥ 0 и из части прямой у =- х при х < 0.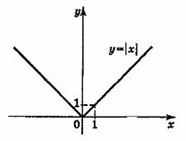



Свойства функции

1.  Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) - начале координат.

2.  Если х ≠ 0, то у > 0, т.е. все точки графика   функции  y = |x|,   кроме   начала координат, лежат над осью абсцисс.

3.   Множеством значений функции y = |x|  является промежуток [0;+∞).

4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| - четная).

5.  На промежутке [0;+∞) функция y = |x|  возрастает.

6. На промежутке (-∞;0] функция y = |x|  убывает.

7.  Наименьшее значение функция принимает в точке х, оноравно 0. Наибольшего значения не существует.

 

6.Функция

Область определения функции: .

Область значений функции: .

График — гипербола.

1. Нули функции.

                             у ≠ 0, нулей нет.

2. Промежутки знакопостоянства,

Если k > 0, то у > 0 при х > 0; у < 0 при х < О.

Если k < 0, то у < 0 при х > 0; у > 0 при х < 0.

3. Промежутки возрастания и убывания.

Если k > 0, то функция убывает при .

Если  k < 0, то функция возрастает при .

4. Четность (нечетность) функции.

Функция нечетная.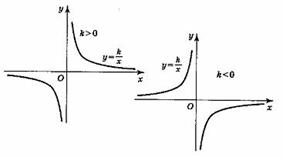



 Практическая часть:

1. 
   Найдите область определения функции
   

2. 
   При каких значениях функция принимает положительные значения?
   

Постройте график функции

3. 
   Постройте график функции и укажите координаты точек пересечения этих графиков.
   
4. 
   Постройте график функции
   

Проходит ли график через точку А(-35, -65)?
Домашнее задание

1. 
   Вычислите координаты точек пересечения параболы и прямой
   
2. 
   Какая из прямых у = 3х - 1, у = 2х + 4 или у = -2х проходит через начало координат? Постройте график этой функции.