Лекция 5. Тема Нелинейная регрессия

• Название: Тема Нелинейная регрессия
• Дата: 16.02.2021
• Размер: 200.5 Kb.
• Имя файла: Лекция 5.doc
• Тип: Документы; #176688

Тема 3. Нелинейная регрессия

1. Модели нелинейной регрессии

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: гиперболы у = a + b/x + , параболы у = а + b  x + c  x² +  и др.

Различают два класса нелинейных регрессий:

– регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

– регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включенным в нее объясняющим переменным могут служить следующие функции:

– полиномы разных степеней: у = а + b  x + c  x² + ; у = а + b  x + c  x² + d  x³ + ;

– равносторонняя гипербола у = a + b/x + .

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

– степенная у = a  x^b  ;

– показательная у = a  b^x  ;

– экспоненциальная у = e^{a + b  x} .

Нелинейная регрессия по включенным переменным не имеет никаких сложностей для оценки ее параметров. Они определяются, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе второй степени

у = а₀ + a₁  x + a₂  x² + ,

заменив переменные x = x₁, x² = x₂, получим двухфакторное уравнение линейной регрессии:

у = а₀ + a₁  x₁ + a₂  x₂ + ,

для оценки параметров которого используется МНК

Соответственно для полинома третьего порядка

у = а₀ + a₁  x + a₂  x² + a₃  x³ + 

при замене x = x₁, x² = x₂, x^З = x₃ получим трехфакторную модель линейной регрессии

у = а₀ + a₁  x + a₂  x₂ + a₃  x₃ + ,

а для полинома k-го порядка

у= а₀ + a₁ x + a₂ x² + … a_k x^k+ 

получим линейную модель множественной регрессии с k объясняющими переменными:

у = а₀ + a₁  x + a₂  x₂ + … a_k  x_k+ .

Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничения в применении полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно меньше однородность совокупности по результативному признаку.

Модели регрессии, нелинейные по оцениваемым параметрам, подразделяются на внутренне линейные и внутренне нелинейные. Если нелинейная модель внутренне линейна, то с помощью соответствующих преобразований она может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цены широко используется степенная функция

,

где y – спрос (количество); x – цена;  – случайная ошибка.

Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры a и b неаддитивно. Однако её можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию e приводит его к линейному виду:

ln y = ln a + b  ln x + ln 

Соответственно оценки параметров a и b могут быть найдены методом наименьших квадратов. В рассматриваемой степенной функции предполагается, что случайная ошибка  мультипликативно связана с объясняющей переменной x. Если же модель представить в виде , то она становится внутренне нелинейной, ибо её невозможно превратить в линейный вид.

Внутренне нелинейной будет и модель вида

,

или модель

,

потому что эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам.

В специальных исследованиях по регрессионному анализу к нелинейным часто относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразования параметров могут быть приведены к линейному виду, относят к классу линейных моделей. Например, экспоненциальную модель y = e^{a + b  x}; ибо, прологарифмировав её по натуральному основанию, получим линейную форму модели

ln y = a + b  x + ln .

Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей итеративной процедуры. Модели внутренне нелинейные по параметрам, могут иметь место в эконометрических исследованиях; однако большее распространение получили модели, приводимые к линейному виду. Решение такого типа моделей реализовано в стандартных пакетах прикладных программ.

По виду преобразования, которое используется для приведения модели к линейному виду, выделяют следующие группы моделей:

1. 
   Двойная логарифмическая модель (и зависимая, и объясняющая переменные заданы в логарифмическом виде). Получается при линеаризации уравнения . Сводится к линейной путем замены U=lnY Z=lnX A=lna: U= A +b · Z
   
2. 
   Полулогарифмические модели - это модели вида
   

- лог-линейная. Получается при линеаризации уравнения . Сводится к линейной путем замены U=lnY : U= a +b · X

- линейно-логарифмическая. Сводится к линейной путем замены Z=lnX : Y= a +b · Z

3. 
   Обратная модель . Сводится к линейной путем замены Z=1/X Y=a+b·Z+
   
4. 
   Степенная модель (полиномиальная) .
   

2. Выбор вида зависимости

При выборе вида зависимости между двумя признаками нагляден графический метод, особенно для монотонных (не имеющих максимумы и минимумы) зависимостей. Наиболее характерные из них представлены на рис.2.4.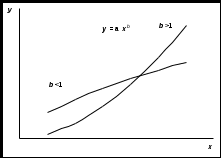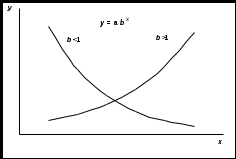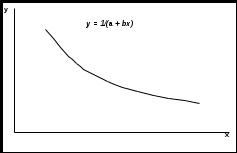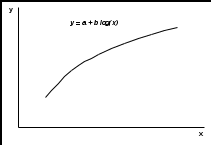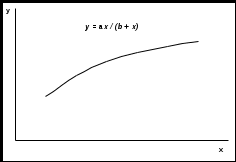





Рис.2.4. Графики монотонных зависимостей

При выборе зависимости во-первых, выбирается кривая, которая наиболее подходит для экспериментальных данных (исходя из аналитических предпосылок, либо визуально по графику), а во-вторых, если затруднительно выбрать одну из нескольких кривых, используют метод средних точек.

В таблице приведены основные типовые формулы, наиболее часто встречающиеся в эконометрических исследованиях. Для каждой зависимости рассчитываются координаты средних точек X_k и Y_k по формулам из таблицы. Средние точки наносят на график и выбирают ту формулу, средняя точка которой лежит ближе всего к экспериментальной кривой.

№		Формула	Xk	Yk	Приведение к линейному виду
1	степенная				U = A + bZ; U = lgY; A = lga; Z = lgX
2	показательная				U = A + BX; U = lgY; A = lga; B = lgb
3	дробно-рациональная				U = a + bX; U = 1/Y
4	логарифмическая				Y = a + bZ; Z = lgX
5	гиперболическая				Y = a + bZ; Z = 1/X
6	функция спроса (Торнквиста)				U = A + BZ; U = 1/Y; Z = 1/X; A = 1/a; B = b/a

3. Определение параметров уравнения регрессии

Рассмотрим нелинейные регрессии по оцениваемым параметрам. Пусть в результате наблюдения получен ряд изучаемого показателяX и Y. По этим значениям можно построить график.

X	x1	x2	…	xn
Y	y1	y2	…	yn

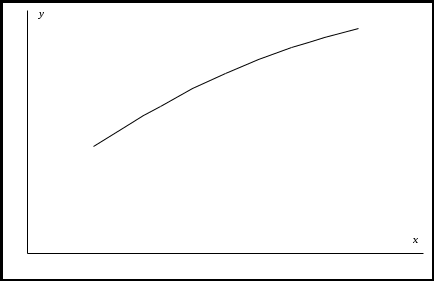Затем необходимо определить параметры выбранной зависимости a и b таким образом, чтобы расчетная кривая лежала как можно ближе к экспериментальной кривой.

Для этого сначала необходимо привести уравнение регрессии к линейному виду. Это преобразование называется линеаризацией. Для этого необходимо ввести замену переменных согласно выбранной модели (в соответствии с таблицей). После введения новых переменных U и Z, необходимо рассчитать параметры A и В этого уравнения.

В качестве критерия близости S выбираем минимум суммы квадратов отклонений между экспериментальными и расчетными значениями. Учитывая, что в каждом конкретном случае линейный вид уравнения различный, запишем этот критерий в универсальном виде:



Для каждой формулы из табл. в этом критерии будут присутствовать разные переменные в зависимости от приведения их к линейному виду. Например, для первой формулы U = lgY; Z = lgX. Тогда система нормальных уравнений для определения параметров линейной зависимости будет иметь вид: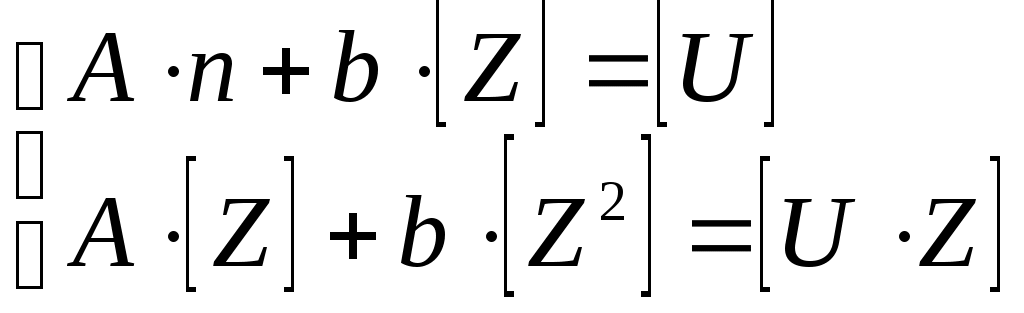

,

где [Z] = Z_i; [U] = U_i; [Z²] = Z_iZ_i; [UZ] = U_iZ_i; n – количество экспериментов; A = lga и b – искомые коэффициенты уравнения (для определения а необходимо выполнить обратное преобразование: a = 10^A).

Для нахождения соответствующих сумм в каждом случае необходимо получить различные вспомогательные таблицы с учетом приведения выражений к линейному виду. Например, для второй формулы из табл.2.3 Z_i = X_i, а U_i = lg(Y_i) и т.д.

Решив эту систему, получаем искомые значения параметров. Следует отметить, что при нахождении параметров других зависимостей необходимо сначала привести их к линейному виду согласно табл.2.3.

Для проверки правильности выполненных действий получаем расчетные значения подстановкой в найденную формулу экспериментальных значений X. Полученные расчетные значения наносим на график с экспериментальными данными и делаем вывод об адекватности.

X	x1	x2	…	xn
Y	y1р	y2р	…	ynр

Рассмотрим зависимость урожайности зерновых культур от количества внесенных удобрений:

Внесено удобрений, ц/га, x	1	2	3	4	5
Урожайность, ц/га, y	6	9	10	12	13

График экспериментальной кривой представлен на рисунке.

Принимаем X₁ = 1, X_n = 5, Y₁ = 6, Y_n = 13. Находим координаты средних точек:

1) ; ;

2) ; Y_k = 8,83;

3) X_k = 3; ;

4) X_k = 2,24; ;

5) ; Y_k = 9,5;

6) X_k = 1,67; Y_k = 8,21.

И наносим их на тот же график.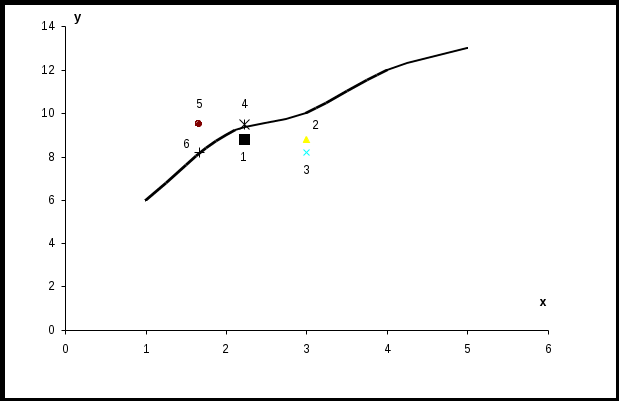



В связи с неровностью исходной кривой выбор зависимости неоднозначен – для учебных целей выбираем формулу 1: Y = a  Х^b. В линейном виде U = A + bZ; U = lg Y; A = lg a; Z = lg X.

Система нормальных уравнений имеет вид: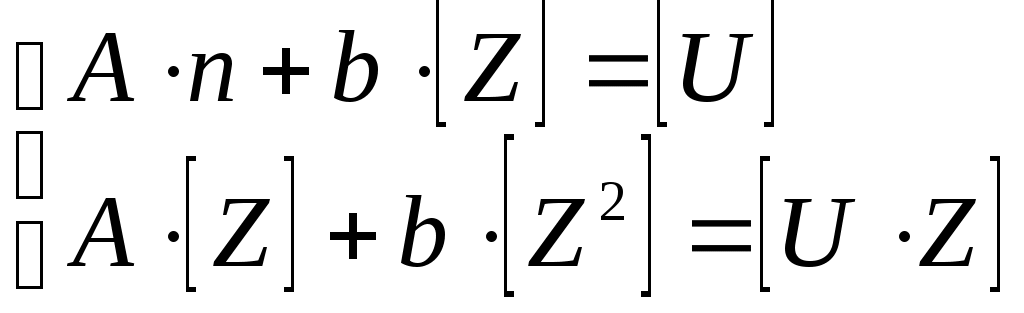



Находим коэффициенты этой системы. Для этого оформляем табл. 2.4

Таблица 2.4. Промежуточные результаты расчета

X	Y	Z = logX	U = logY	Z 2	Z  U	Y р
1	6	0,00	0,78	0,00	0,00	6,14
2	9	0,30	0,95	0,09	0,29	8,52
3	10	0,48	1,00	0,23	0,48	10,33
4	12	0,60	1,08	0,36	0,65	11,84
5	13	0,70	1,11	0,49	0,78	13,16
		2,08	4,93	1,17	2,19

Решаем систему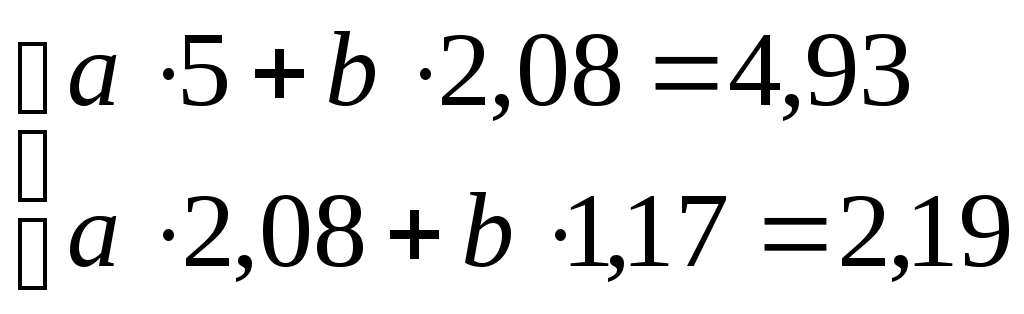



; .

Так как в линейном виде участвует переменная A, необходимо перейти к исходной переменной а, по формуле а = 10^А = 10^0,788 = 6,136. В итоге получаемY = 6,136  Х^0,474.

Расчетные значения по полученному уравнению регрессии приведены в последнем столбце табл.2.4. исходные и расчетные значения урожайности приведены на следующем графике: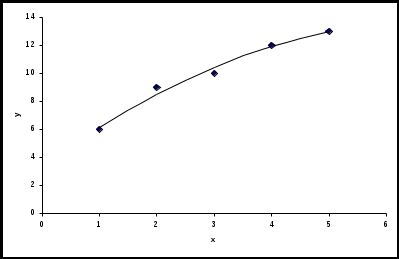



По взаимному расположению двух кривых можно сделать вывод о достаточно хорошей сходимости полученного уравнения (далее будут применены статистические критерии сходимости).

Содержимое табл.2.4 зависит от выбранной формулы, в ней могут быть столбцы с разными Х, Y, Z, и U, конкретные значения которых зависят от соответствующих преобразований в последнем столбце табл.2.3. Например, для 6-й формулы из табл.2.3 вместо X в табл.2.4 будет значение Z = 1/X, а вместо Y – U = 1/Y. Соответственно изменятся и столбцы Z² и U  Z вместо Y  Z. Преобразуется и система нормальных уравнений.