Метод Белого ящика. Белый ящик. Тестирование методом Белый ящик
 Скачать 96.31 Kb. Скачать 96.31 Kb.
|
|
Тестирование методом «Белый ящик» Тестирование белого ящика предполагает, что проверяющий располагает исходным кодом модуля. Будем предполагать, что текст программы состоит из последовательности выполняемых операторов (присваивания, печати, вызова функций и пр.), условных операторов, операторов выбора и циклов. На языке блок-схем эти элементы изображаются: 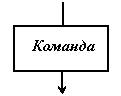 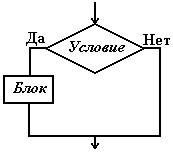 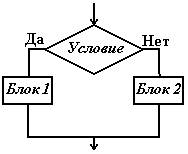 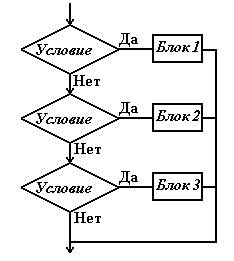 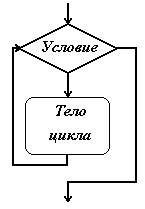 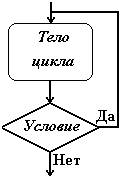 По собранной из таких элементов блок-схеме можно наметить различные стратегии и методы тестирования. 1. Метод покрытия операторов. Этот метод требует написания такого количества тестов, чтобы при выполнении их всех каждый оператор был выполнен хотя бы один раз. Рассмотрим для примера блок-схему: 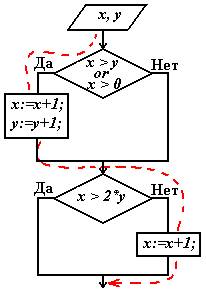 Очевидно, что тест x=1, y=1 покроет все операторы, т. к. вычисление поедет по траектории, помеченной красным пунктиром. 2. Метод покрытия решений (путей). Под решениями здесь подразумеваются высказывания в операторых условного перехода, выбора, цикла, взятые целиком. Эти всказывания часто составлены из более простых – элементарных высказываний, которые мы будем до концы параграфа называть условиями. Так, в примере “x>y or x>0” – решение, а его части “x>y” и “x>0” – условия. Метод покрытия решений требует такого количества тестов, чтобы при выполнении их всех по каждой траектории, соединяющей соседние элементы блок-схемы вычисление прошло хотя бы один раз. Это означает, что каждое решение должно принимать как истинные, так и ложные значения. Именно это обеспечивает использование всех путей, выходящих из точек ветвления. Что касается операторов выбора, к ним это также относится. Для того, чтобы сохранит общность рассуждений, надо только переделать их (мысленно) в эквивалентную цепочку условных операторов. Для нашего примера к тесту x=1, y=1 надо добавить еще один. Например, x = -3, y = -2. 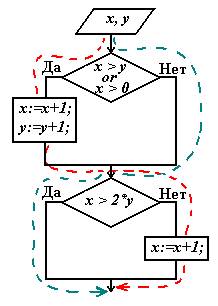 Для него вычисление пойдет по зеленой траектории и все пути будут покрыты. Очевидно, что метод покрытия решений гарантирует покрытие операторов. 3. Метод покрытия условий. В нашем примере имеется решение (x > y) or (x > 0), состоящее из двух условий “x > y” и “x > 0”. Для первого теста в п.2 это решение истинно, для второго теста – ложно. Для первого теста оно истинно потому, что истинна его вторая его часть. Для второго теста оно ложно, потому, что оба суждения ложны. Получается, что для обоих тестов условие x > y ложно. Такое тестирование явно ущербно. Метод покрытия условий состоит в таком подборе тестов, когда каждое условие (элементарное суждения в условных операторах) принимает как истинное так и ложное значение. В нашем примере имется три условия: “x > y”, “x > 0” и “x > 2*y”. Тесты: x = 1, y = 1 и x = 0, y = -1 покрывают все эти условия. 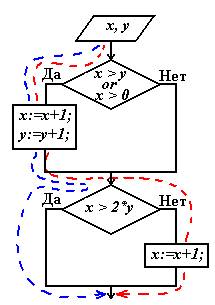 Но, как видим, этот метод не гарантирует покрытия решений. 4. Метод покрытия решений/условий. Это такой набор тестов, который покрывает и условия и решения одновременно. В нашем примере такими тестами будут: x=1, y=0 и x = -3, y = -2. Схема, как уже было  Очевидно, что метод покрытия решений/условий гарантирует покрытие и операторов, и решений и условий. Тем не менее и он имеет недостатки. 5. Метод комбинаторного покрытия условий. Недостатком метода решений/условий является то, что некоторые условия во всех тестированиях могут вообще не вычисляться. Например, для (x>y)||(x>0) компилятор языка C создаст такую программу, которая не станет вычислять (x>0), если обнаружит, что (x>y). Если программист хочет проверить все условия в решениях, он должен озаботиться подобными затруднениями. Для того, чтобы приготовить нудное множество тестов, нет нужды анализировать логическую структуру решений. Если она не простая, да к тому же написана другим программистом, это может занять слишком много времени. Надо просто выписать все условия всех решений и создать тесты, реализующие все возможные комбинации истинности условий в каждом решении. Посмотрим теперь, какие условия и как будут вычисляться с помощью тестов п.4. При x=1, y=0 будут вычислены только: “(x > y) ” = true , “(x>2*y)” = false. При x = -3, y = -2 будут вычислены: “(x > y) ” = false , “(x>0)” = false, “(x>2*y)” = true. Таким образом вычисления “(x>0)” с результатом true не будет ни разу. Эту неприятность можно устранить, если добавить еще один тест. Например, x = 1, y=2. В данном случае больше тестов не нужно, но мы это видим, “заглянув” в логическую структуру высказывания (x>y)||(x>0). Если же этого не делать, то надо просто позаботиться о всех комбинациях истинности для (x>y) и для (x>0). Иначе – заполнить таблицу
до конца, добавив, например, в пустую клетку тест x=0, y= -1. Все выше сказанное создает впечатление, что если в модуле имеется n условий, то данный метод требует придумывания 2n тестов, что уже при n=10 совершенно не подъемно. Однако это не так. Реально 10 условий распределяются по решениям. Например так: if(F1(A0,A1,A2)) … if(F2(A2,A3,A4)) … if(F3(A5,A6,A7,A8)) … if(F4(A8,A9)) … Видим, что условия разбиваются на два независимых класса: {A0,A1,A2,A3,A4} и {A5,A6,A7,A8,A9}. Теперь надо постараться так заполнить таблицы
значениями истинности, чтобы для каждого набора {A0,A1,A2},{A2,A3,A4},{A5,A6,A7,A8},{A8,A9} релизовались все возможности. Вот эти таблицы, где для краткости true=1, false=0.
Таким образом понадобится только 16 тестов. Безусловно, метод комбинаторного покрытия условий гарантирует покрытие и операторов, и решений и условий. |
