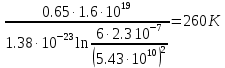|
|
Дефекты. Дефекты теория. Точечные дефекты
Дефекты
Многие свойства материалов в сильной степени чувствительны к отклонениям от идеальной кристаллической структуры. Во всех материалах имеются различные несовершенства или дефекты. Влияние дефектов не всегда оказывается неблагоприятным и некоторые особые свойства материалов можно сознательно изменять, вводя в них контролируемые количества определенных дефектов.
Под термином «кристаллический дефект» понимается нерегулярность в построении кристаллической решетки с размерами порядка атома. Классификация кристаллических дефектов основывается на геометрической форме или размерности дефекта. Точечные дефекты(несовершенства на атомном уровне) в твердом теле можно разделить на три основные категории: примеси (чужеродные атомы), собственные точечные дефекты (вакансии и межузельные атомы) и их комплексы.
Точечные дефекты в металлах
П
ростейшим случаем собственного дефекта является вакансия, т.е. отсутствие атома в узле кристаллической решетки и наличие дополнительного атома на поверхности кристалла, причем общее число атомов в кристалле не изменяется. Все кристаллические твердые тела содержат вакансии и создать материал, в котором бы вообще отсутствовали вакансии, невозможно. Неизбежность возникновения вакансий можно объснить, исходя из принципов термодинамики. В сущности появление вакансий приводит к увеличению энтропии (неупорядоченности) кристалла.
Рис.5.1 Двумерное представление вакансий и междоузлий
Равновесное число вакансий в заданном объеме материала зависит от температуры и выражается формулой:

В этой формуле N– это общее число мест, занимаемых атомами, Q- энергия, необходимая для образования вакансии, T- абсолютная температура, выраженная в Кельвинах, k- газовая постоянная или постоянная Больцмана. Ее значение составляет 1.38∙ 10-23 Дж/атом∙К или 5.62∙10-5 эв/атом∙К.
Таким образом, число вакансий растет экмспоненциально уведичивается с повышением температуры. Для многих металлов относительное содержание вакансий непосредственно вблизи температуры плавления составляет величину порядка 10-4, так что одно место из 10000 остается незаполненным.
ЗАДАЧА 5.1. Расчет количества вакансий при заданной температуре
Рассчитайте равновесное количество вакансий в одном кубическом метре меди при 1000 °С. Энергия образования вакансии равна 0,9 эВ/атом. Атомный вес меди 63,5 г/моль, ее плотность при 1000 °С составляет 8,40 г/см3.
Решение
Задача решается с помощью формулы . Прежде всего, однако, необходимо найти значение N— число мест, занимаемых атомами в 1 м3. Исходя из
величины атомного веса Аcu, ее плотности 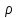 и числа Авогадро NA находим: и числа Авогадро NA находим:
N= 3 Отсюда находим, что число вакансий при 1000 °С (1273 К) составляет 3 Отсюда находим, что число вакансий при 1000 °С (1273 К) составляет
Nv = N  exp (-Q/kT)= 8.08 exp (-Q/kT)= 8.08 1028exp 1028exp вакансий/м3 вакансий/м3
Собственный междоузельныйатом - это атом (или ион), который с поверхности попадает внутрь кристалла и размещается в некотором промежуточном положении в решетке. При этом вблизи междоузельного атома возникают сжатия и растяжения кристаллической решетки. Дефекты такого типа показаны на рис.1. Такие междоузельные атомы создают довольно большие искажения в окружающей их кристаллической решетке, поскольку они обычно значительно больше, чем свободное пространство. Поэтому вероятность возникновения такого рода дефектов невысокая, и они существуют в концентрациях меньших, чем вакансии.
Точечные дефекты в керамике
Точечные дефекты могут существовать в керамике. Поскольку в керамике содержатся ионы двух видов, дефекты могу возникать в любом из них. Например, в NaCl и вакансии и междоузлия могут относиться и ионам как Na+ , так и Cl-. При этом маловероятно, что большое количество междоузлий возникнет в структуре анионов Cl-. Эти анионы обладают большими размерами, поэтому свободного пространства между ними мало и возникновение таких дефектов потребовало бы больших искажений решетки.
 Вакансии катионов и анионов и междоузлие катионов показано на рисунке 5.2 Вакансии катионов и анионов и междоузлие катионов показано на рисунке 5.2
Выражение «структурные дефекты» часто используют для обозначения различных типов и концентраций дефектов в расположении атомов в керамике. В этом случае должен соблюдаться принцип нейтральности. Под электронейтральностью понимают равенство числа положительных и отрицательных зарядов в материале. Вследствие этого дефекты в керамике никогда не бывают единичными. Один из дефектов состоит в образовании пары – вакансия катиона и междоузлие катиона. Это дефекты Френкеля (рис.5.3). Можно полагать такие пары появляются тогда, когда катион покидает свое нормальное положение и смещается в межузлие. При этом не происходит изменения заряда, поскольку катион сохраняет свой положительный заряд.
Другой тип дефектов, известный под названием «дефект Шоттки», встречается в материалах типа АХ, представляет собой парную вакансию аниона и катиона. Он также схематически показан на рис. 5.37 Можно полагать, что такой дефект возникает при удалении одного катиона и одного аниона из внутренней части кристалла. Оба эти иона имеют один и тот же заряд, и поскольку число вакансий катионов и анионов одинаково, кристалл 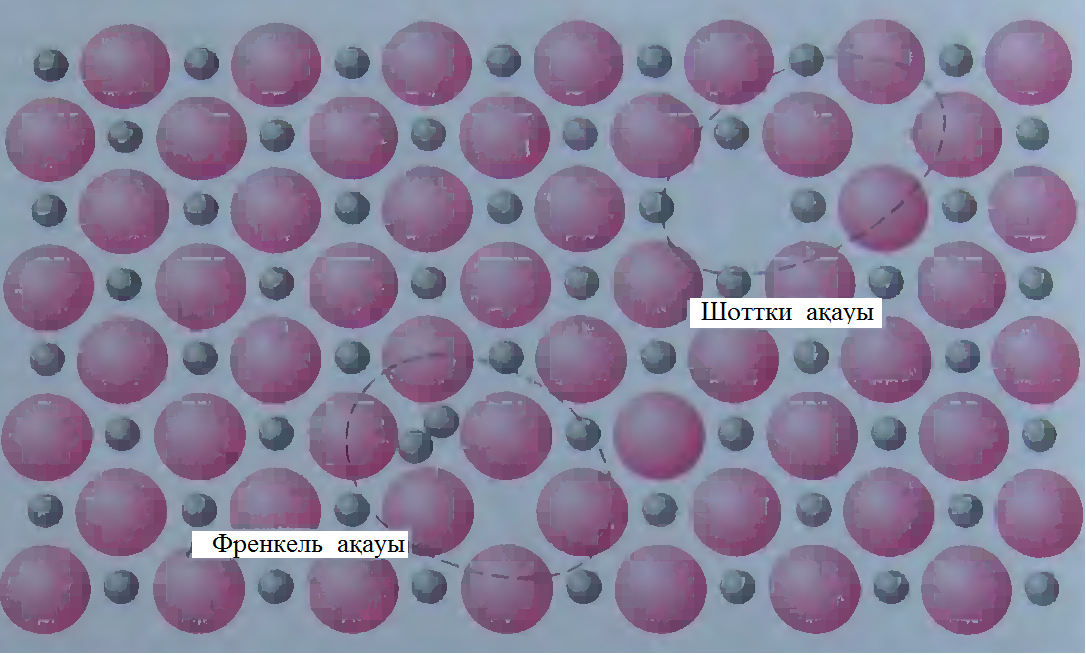 остается электронейтральным. остается электронейтральным.
 Отношение катионов и анионов не изменяется при образовании дефектов Френкеля и Шоттки. Если никаких других дефектов не образуется, то в таком случае говорят о стехиометрии вещества. Нестехиометрические составы могут существовать в керамике, в которой имеют место два электронных состояния для ионов одного типа. Например, FeO, поскольку железо может существовать в виде Fe2+ и Fe3+ . Количество ионов разного типа зависит от температуры и давления кислорода в окружающей среде. Образование ионов Fe3+ нарушает электронейтральность кристалла, так как вносит избыточный положительный заряд +1, который должен быть скомпенсирован образованием дефекта того или иного типа. Это может происходить путем появления вакансии Fe2+ иона , т.е. удалением двух положительных зарядов, уравновешивающих образование двух ионов Fe3+. Отношение катионов и анионов не изменяется при образовании дефектов Френкеля и Шоттки. Если никаких других дефектов не образуется, то в таком случае говорят о стехиометрии вещества. Нестехиометрические составы могут существовать в керамике, в которой имеют место два электронных состояния для ионов одного типа. Например, FeO, поскольку железо может существовать в виде Fe2+ и Fe3+ . Количество ионов разного типа зависит от температуры и давления кислорода в окружающей среде. Образование ионов Fe3+ нарушает электронейтральность кристалла, так как вносит избыточный положительный заряд +1, который должен быть скомпенсирован образованием дефекта того или иного типа. Это может происходить путем появления вакансии Fe2+ иона , т.е. удалением двух положительных зарядов, уравновешивающих образование двух ионов Fe3+.
Рисунок . Схематическое изображение поведения вакансии Fe2+ в кристалле FeO , являющееся следствием образования двух ионов Fe3+
В этом случае кристалл перестает отвечать условию стехиометричности, поскольку в нем содержится на один ион кислорода больше, чем Fe (рис.).
Однако кристалл остается электронейтральным. Явления такого рода довольно обычны среди химических соединений.
Контрольный вопрос.
Могут ли дефекты Шоттки возникать в кристалле К2О? Если могут, то кратко объясните , каковы дефекты этого типа. Если нет, то объясните почему.
Равновесное число дефектов Френкеля или Шоттки увеличивается с ростом температуры аналогично вакансиям. Температурная зависимость числа дефектов Френкеля описывается формулой: описывается формулой:
 , (5.3) , (5.3)
где  – энергия, необходимая для образования каждого дефекта Френкеля, N- число мест в решетке, – энергия, необходимая для образования каждого дефекта Френкеля, N- число мест в решетке, 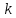 - постоянная Больцмана, Т- абсолютная температура. Коэффициент 2 в знаменателе появляется потому, что для образования дефекта Френкеля необходимо наличие двух дефектов (отсутствующего катиона и междоузельного катиона). - постоянная Больцмана, Т- абсолютная температура. Коэффициент 2 в знаменателе появляется потому, что для образования дефекта Френкеля необходимо наличие двух дефектов (отсутствующего катиона и междоузельного катиона).
Аналогично записанному выше выражению, температурная зависимость числа дефектов Шоттки в кристаллах типа АХ выражается следующим образом:
 , (5.4) , (5.4)
где  - энергия, затрачиваемая на образование дефекта Шоттки. - энергия, затрачиваемая на образование дефекта Шоттки.
Задача 2. Подсчитайте число дефектов Шоттки в кристалле КCl. Рассчитайте число дефектов Шотки в одном кубическом метре хлорида калия при 5000С. Энергия образования Шоттки равна 2.6 эВ, плотность КCl при 5000 С 1.955 г/см3.
Решение.
Решение поставленной задачи основано на использовании общей формулы:
Ns=Nexp( ), (1) ), (1)
где Qs - энергия, затраченная на образование дефекта Шоттки.
Однако, прежде всего необходимо определить n – число мест в решетке, содержащееся в 1 м3. Найти эту величину можно, используя модифицированную форму уравнения, а именно: N= , ,
где Na -число Авагадро (6.02∙1023 атом/моль), ρ-плотность, АК и АCl – атомные веса калия и хлора (т.е. 39.1 и 35,45 г/моль соответственно). Тогда:
N=
Теперь, используя полученные величины, с помощью формулы (1)
Ns=(1.58∙1028)exp
Примеси в твердых телах.
Примеси в металлах.
Чистые металлы, полностью состоящие из атомов одного типа, не могут существовать. В них всегда присутствуют примеси или атомы другого типа, и некоторые из них образуют дефекты кристаллической решетки. На самом деле даже с помощью техники трудно очистить металл до содержания однотипных атомов выше 99.9999%. А при такой чистоте в одном кубическом метре вещества содержатся 1022-1023 посторонних атомов. Большинство обычных металлов не обладают такой чистотой и представляют собой сплавы, в которых атомы другого типа вводятся в заметных количествах с целью улучшить либо механические свойства материала,либо повысить его стойкость к коррозии. Например, обычно под техническим серебром имеется в виду сплав, содержащий 93.5% серебра и 7.5% меди. В нормальных условиях чистое серебро обладает высокой коррозионной стойкостью, но это очень мягкий материал. Добавление меди значительно повышает механическую прочность без заметного ухудшения сопротивления коррозии. Введение посторонних атомов в металл приводит к образованию твердых растворов и/или формированию новой фазы, что определяется видом примеси, ее концентрацией и температурой.
Твердые растворы.
Положения, в которых располагаются посторонние атомы, могут быть двух типов: они могут замещать атомы основного кристалла (матрицы) или внедряться между ними. При этом первоначальная структура кристалла сохраняется. Степень растворения постороннего вещества в основном материале определяют следующие факторы:
Размер атомов. Заметные количества растворяемого вещзества могут поглощаться основныым материалом только в том случае, если разница в размерах атомных радиусов обоих компонентов не превышает 15%. В противном случае атомы растворяемого вещества сильно искажали бы кристаллическую решетку и образовывали бы новую фазу.
Структура кристалла. Для того, чтобы произошло растворение, структура кристаллической решетки обоих компонентов должна быть одинаковой.
Электроотрицательность. Чем больше электроположительность одного компонента и электроотрицательность другого, тем больше вероятность того, что они образуют интерметаллическое соединение, а не раствор.
Валентность. При прочих равных условиях тенденция одного металла растворить другой тем выше, чем больше валентность растворяемого вещества.
В качестве примера твердого раствора замещения можно привести сплав меди и никеля. Эти два элемента полностью растворимы друг в друге при любом соотношении компонентов. Атомные радиусы меди и никеля равны 0.128 и 0.125 нм соответственно, оба элемента образуют гранецентрированную решетку и их электроотрицательности равны 1.9 и 1.8. Валентность мели -1, никеля-2.
Что касается растворов внедрения, то в этом случае посторонние атомы заполняют пустоту между атомами. Для металлов с довольно плотной упаковкой атомов эти междоузельные пространства сравнительно невелики. Соответственно атомные размеры постороннего вещества должны быть существенно меньшими, чем атомы матрицы. Как правило, концентрация вещества, образующего атомы внедрения, мала (не более 10%).
Углерод, вводимый в железо, образует твердый раствор внедрения. При этом максимальная концентрация углерода не превышает 2%. Атомный радиус углерода много меньше, чем железа – 0.071нм по сравнению с 0.124 нм.
Примеси в керамике
Посторонние примесные атомы могут образовывать твердые растворы в керамике. При этом возможно образование растворов обоих типов – замещения и внедрения (рис.). Если происходит внедрение посторонних атомов, то их размер должен быть небольшим по сравнению с атомами основного вещества. Поскольку в керамике имеются положительно и отрицательно заряженные ионы, замещение посторонним атомом происходит таким образом, что он занимает место иона, наиболее близкого ему по заряду.
Для того, чтобы примесный ион мог образовать раствор замещения или внедрения, его размер и заряд должны быть максимально близки к соответствующим характеристикам иона основной решетки. Если посторонний ион имеет заряд отличный от заряда иона матрицы, то эта разница должна быть скомпенсирована, чтобы сохранить электронейтральность материала в целом.

Задача. Оцените, какие типы точечных дефектов возможны в хлориде натрия из-за присутствия ионов Са2+.
При требовании сохранения электронейтральности, образование каких точечных дефектов возможно в кристаллах NaCl при замещении ионов Na+ на Са2+? Какое количество дефектов образуется в расчете на один ион Са2+?
Решение. Замещение ионов Na+на Са2+ приводит к появлению одного избыточного положительного заряда. Достижение условия электронейтральности требует, чтобы был устранен один положительный заряд или добавлен один отрицательный заряд. Удаление одного положительного заряда достигается образованием вакансии на месте иона Na+ . Вместо этого может быть внедрен один отрицательный ион Cl-. Любой из этих вариантов позволяет нейтрализовать ион Са2+. Однако образование дефекта такого типа крайне маловероятно.
Задача. Какие точечные дефекты возможны в MgO, который выступает в качестве примеси к Al2O3? Сколько ионов Mg2+ необходимо добавить для того, чтобы образовались эти дефекты?
Дислокации. Точечные дефекты, например вакансии, вызывают нарушения решетки лишь в окрестности одного узла решетки (или
в крайнем случае нескольких соседних узлов). Дислокации же приводят к линейным нарушениям структуры. В общем случае дислокации в кри- сталле могут иметь любую форму, однако понять их строение можно на примере двух простейших типов дислокации: краевой и винтовой.
В случае чисто краевой дислокации одна из атомных плоскостей внутри кристалла обрывается, напоминая лезвие ножа при нарезании сыра.
Этот тип дислокаций иллюстрирует рис. 8.1, а. Сдвиг в решетке (опре- деляемый вектором Бюргерса b ) перпендикулярен линии дислокации (направлению последнего ряда атомов в полуплоскости). Длина вектора
Бюргерса равна целому числу единичных векторов решетки. В случае
винтовой дислокации (рис. 8.1, б) одна часть решетки смещена относи- тельно другой в направлении, параллельном линии дислокации. Чтобы мысленно получить винтовую дислокацию, надо сначала сделать в со- вершенном кристалле надрез, а затем одну сторону надреза поднять от- носительно другой на величину одного или нескольких единичных век- торов решетки и в таком положении состыковать обе стороны разреза.
Для описания такого сдвига также пользуются вектором Бюргерса, который всегда равен целому числу единичных векторов решетки, а для чисто винтовой дислокации к тому же параллелен ее оси.В общем случае дислокация в реальном кристалле может быть представлена как результат наложения краевой и винтовой компонент, п
ричем соотношение между ними меняется вдоль линии дислокации. Заметим, однако, что вектор Бюргерса на всем протяжении дислокации не меняется. Дислокация не может обрываться внутри кристалла; она либо имеет вид замкнутой петли, либо оканчивается на свободных по- верхностях кристалла или межкристаллитных границах. Во многих слу- чаях следы выхода дислокации на поверхность кристалла можно обна- ружить с помощью химического травления, которое сильнее всего действует на напряженные области, при этом появляются ямки травле-ния, ограниченные кристаллографическими плоскостями.
Рис.8.1.Двавидапростыхдислокаций:
а - краеваядислокация;б -винтоваядислокация
В
ажной характеристикой наличия в кристалле дислокаций является плотность дислокаций N D(размерность N Dравна обратному квадрату длины). Она определяется как число дислокаций в единице объема и ха- рактеризует степень совершенства кристалла.
Рис.5.8. Положение атомов вокруг краевой дислокации.
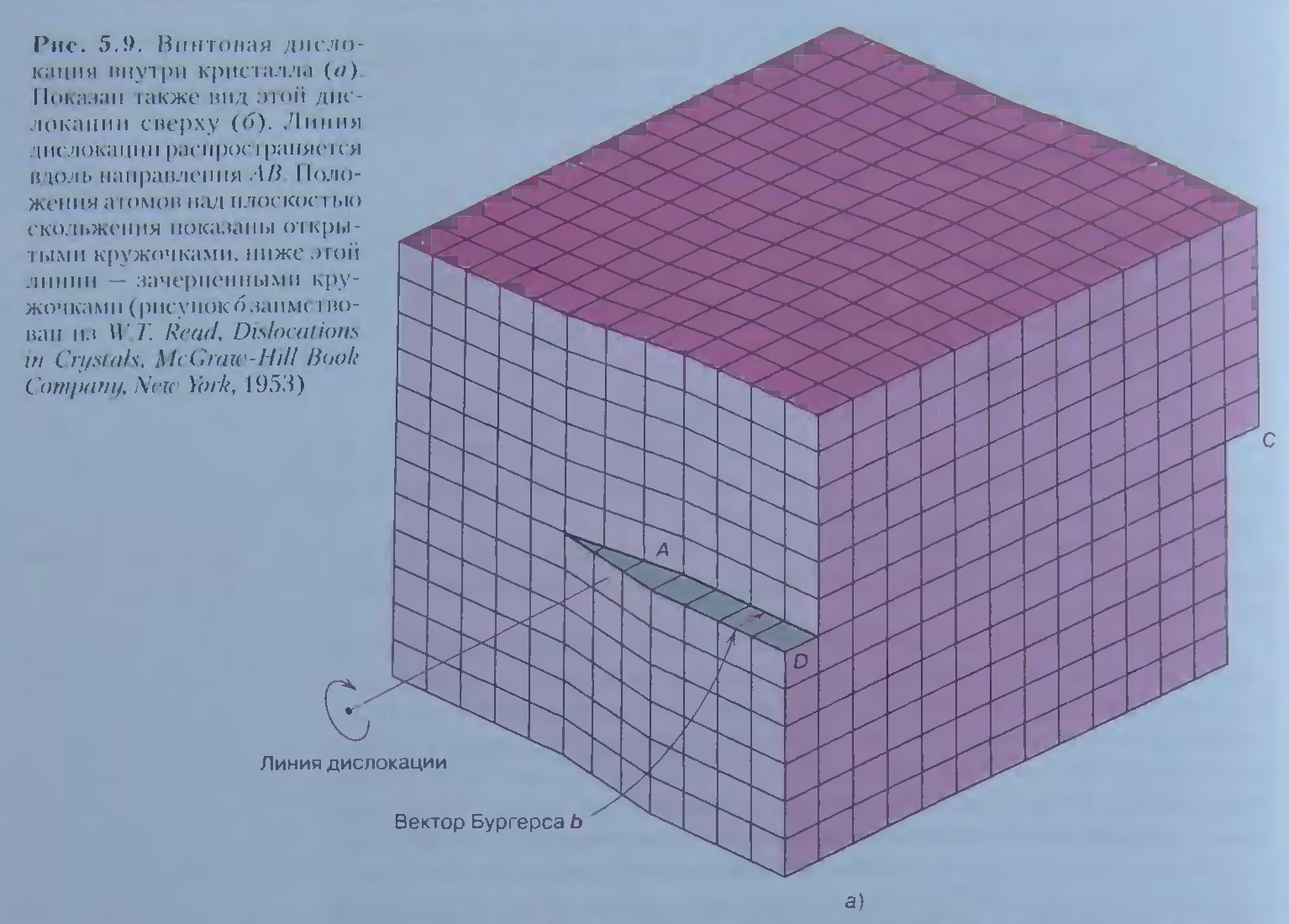 
Рисунок 5.9. Винтовая дислокация внутри кристалла (а). Вид дислокации сверху (б). Линия дислокации распространяется вдоль направления АВ. Положения атомов над плоскостью скольжения показаны открытыми кружочками, ниже этой линии- закрашенные кружочки
Явление диффузии.Тепловые колебания атомов в твердых телах сводятся в основном к колебаниям с малой амплитудой, которые они совершают около средних положений равновесия. Однако кинетическая энергия атомов вследствие их взаимодействия с соседними атомами не остается постоянной. Даже в том случае, когда средняя кинетическая энергия атомов мала, согласно максвелловскому закону распределения скоростей, в кристалле всегда найдется некоторое число атомов, кинетическая энергия которых достаточно велика. Такой атом может сорваться со своего равновесного положения и, преодолев потенциальный барьер, созданный окружающими его атомами, перейти в некоторое но вое свободное положение равновесия. При этом атом теряет избыточную энергию, отдавая ее атомам кристаллической решетки. Через неко торое время атом снова может набрать достаточную энергию, чтобы вырваться из нового окружения и перейти в соседнее. Такие перемещения атомов, обусловленные тепловым движением, и составляют основу диффузионных процессов в твердых телах. Диффузию, ограничиваю-
щуюся перемещением атомов одного элемента в решетке другого, называют атомной. Простым случаем атомной диффузии является самодиффузия - перемещение атомов элементов в своей же собственной кристаллической решетке. В идеальной кристаллической решетке, в которой атомы совершают лишь колебательные движения около своих положений равновесия, процессы диффузии маловероятны. Диффузионное перемещение примесных атомов или собственных атомов решетки всегда связано с наличием в ней простых дефектов - вакансий, междоузельных атомов, дивакансий - и других более сложных дефектов - дислокаций, границ раздела, вакансионных и примесных кластеров (скоплений). Из-за теплового движения при любой температуре происходит непрерывное «перемешивание» атомов, составляющих твердое тело. Скорость «перемешивания» при наличии в решетке вакантных узлов, выражаемая вероятностью перехода атома из одного равновесного положения в другое, вследствие статисти ческого характера процесса изменяется с температурой по экспоненциальному закону:
 , () , ()
где Em - высота потенциального барьера (энергия миграции вакансии), который должен преодолеть атом, чтобы перейти из одного положения равновесия в другое;  1013 с-1 - собственная частота колебаний атома. При данной температуре вероятность Рm определяется значением Еm, зависящим от прочности связи атомов в решетке. Вероятность перехода атома из узла в вакансию должна быть обратно пропорциональна времени «оседлой» жизни атома (вакансии) в узле:
 , () , ()
где  - период собственных колебаний атома, соответствующий максимальной частоте в акустическом спектре, и по порядку величины, равной 10-13 с. Чем выше температура тела, тем меньше время нахожде ния атома в узле. Средняя скорость, с которой вакансия движется по кристаллу - период собственных колебаний атома, соответствующий максимальной частоте в акустическом спектре, и по порядку величины, равной 10-13 с. Чем выше температура тела, тем меньше время нахожде ния атома в узле. Средняя скорость, с которой вакансия движется по кристаллу
 () ()
Концентрация вакансий зависит от температуры:
 , () , ()
где ЕV - энергия образования вакансии. Коэффициент диффузии вакансий
DV в кристаллах:
 () ()
где  - средняя длина свободного пробега частицы; - средняя длина свободного пробега частицы;  - время между двумя столкновениями. Элементарные перемещения в твердом теле имеют одно и то же значение - время между двумя столкновениями. Элементарные перемещения в твердом теле имеют одно и то же значение  . Тогда: . Тогда:
 () ()
Аналогичные рассуждения относятся и к перемещениям атомов по междоузлиям. Перемещение атома из одного междоузлия в соседнее происходит с большей скоростью, поскольку барьеры между междоузлиями понижены по сравнению с барьерами между атомами, сидящими в узлах, и всегда рядом с диффундирующим атомом имеется готовое незанятое междоузлие. Полная вероятность Р того, что одновременно рядом с атомом окажется вакансия и атом совершит перескок в эту вакансию, равна произведению вероятностей:
 , () , ()
где Q=Em+ EV - энергия активации процесса самодиффузии.
Коэффициент диффузии атома по вакансиям:
 () ()
где предэкспоненциальный множитель . .
В реальной ситуации процессы диффузии протекают много сложнее и одновременно могут действовать не один, а сразу несколько механизмов. Для качественного метода расчета диффузии А. Фик использовал уравнение теплопроводности, выведенное Фурье. Он исходил из гипотезы, что в изотропной среде количество диффундирующего вещества, проходящее за единичное время через единичную площадь поперечного сечения, пропорционально градиенту концентрации С, измеряемому по нормали к этому сечению:
 () ()
Это первый закон Фика для стационарного потока. Здесь J - плотность тока диффундирующих атомов; С - их концентрация; 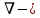 оператор градиента. В общем случае диффузия анизотропна и коэффициент диффузии D - тензор второго ранга – равен: оператор градиента. В общем случае диффузия анизотропна и коэффициент диффузии D - тензор второго ранга – равен:
 () ()
Для одномерной диффузии и изотропной среды уравнение Фика имеет вид:

Так как С характеризует градиент вещества в единичном объеме, то коэффициент диффузии имеет размерность см2 /с или м2/с. Для нестационарного потока второй закон Фика получаем исходя из следующих соображений. Скорость накопления диффундирующего вещества в данном элементе объема является разностью между приходящими и выходящими потоками за единичное время. Рассмотрим две параллельные плоскости, площадь каждой из которых равна единице; а расстояние между ними составляет dx. Поток через первую плоскость равен 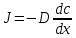 , а поток через вторую плоскость , а поток через вторую плоскость 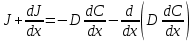 . Тогда разность потоков . Тогда разность потоков
 Но Но  равно взятой с обратным знаком скорости изменения концентрации т.е. равно взятой с обратным знаком скорости изменения концентрации т.е.  . Таким образом, . Таким образом,
 () ()
При условии, что коэффициент диффузии не зависит от концентрации, т. е. является величиной постоянной, получен второй закон Фика для одномерной диффузии в дифференциальной форме:
 () ()
где С = С(х,t) - зависит от времени t и глубины диффузии х. Для диффузии в трех измерениях в изотропной среде:
 () ()
Основным источником информации о параметрах диффузии
в твердых телах является эксперимент. В практике экспериментального
исследования процессов диффузии примесей в твердых телах используют решения уравнения второго закона Фика для одномерного случая при определенных для конкретной физической задачи начальных и граничных условиях.
Пример4. Диффузионные константы лития в кремнии равны
D0= 2,310–7 м 2/с и Q= 0,65 эВ. Рассчитать температуру, при которой атом лития, растворенный в кремнии, будет совершать один прыжок за одну секунду.
Решение: Частота перемещения атома fсвязана с коэффициентом диффузии следующим соотношением  . С другой стороны . С другой стороны 
Тогда

После решения полученного уравнения относительно Т:
T= 
T=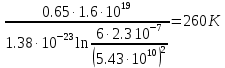
Для образования вакансии в алюминии требуется энергия пример-
но 0,75 эВ. Сколько существует вакансий на один атом кристалла в состоянии термодинамического равновесия при комнатной темпе- ратуре? При 600 °С?
Рассчитать отношение числа дефектов по Шоттки к числу дефектов по Френкелю при комнатной температуре, если энергия для образо- вания вакансии 0,75 эВ, а для образования дефекта внедрения 3 эВ.
Оценить величину коэффициента диффузии радиоактивного натрия в обычном натрии при комнатной температуре, если высота потен-
циального барьера, который надо преодолеть атому, чтобы перейти в новое положение равновесия, равна 0,5 эВ. Частота колебаний атома 1012 Гц.
ПЕРЕВЕСТИ |
|
|
 Скачать 2.94 Mb.
Скачать 2.94 Mb.


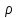 и числа Авогадро NA находим:
и числа Авогадро NA находим:  3 Отсюда находим, что число вакансий при 1000 °С (1273 К) составляет
3 Отсюда находим, что число вакансий при 1000 °С (1273 К) составляет
 exp (-Q/kT)= 8.08
exp (-Q/kT)= 8.08 вакансий/м3
вакансий/м3 


 описывается формулой:
описывается формулой: , (5.3)
, (5.3) – энергия, необходимая для образования каждого дефекта Френкеля, N- число мест в решетке,
– энергия, необходимая для образования каждого дефекта Френкеля, N- число мест в решетке, 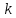 - постоянная Больцмана, Т- абсолютная температура. Коэффициент 2 в знаменателе появляется потому, что для образования дефекта Френкеля необходимо наличие двух дефектов (отсутствующего катиона и междоузельного катиона).
- постоянная Больцмана, Т- абсолютная температура. Коэффициент 2 в знаменателе появляется потому, что для образования дефекта Френкеля необходимо наличие двух дефектов (отсутствующего катиона и междоузельного катиона).  , (5.4)
, (5.4) - энергия, затрачиваемая на образование дефекта Шоттки.
- энергия, затрачиваемая на образование дефекта Шоттки. ), (1)
), (1) ,
,






 , ()
, ()
 , ()
, () - период собственных колебаний атома, соответствующий максимальной частоте в акустическом спектре, и по порядку величины, равной 10-13 с. Чем выше температура тела, тем меньше время нахожде ния атома в узле. Средняя скорость, с которой вакансия движется по кристаллу
- период собственных колебаний атома, соответствующий максимальной частоте в акустическом спектре, и по порядку величины, равной 10-13 с. Чем выше температура тела, тем меньше время нахожде ния атома в узле. Средняя скорость, с которой вакансия движется по кристаллу ()
() , ()
, () ()
() - средняя длина свободного пробега частицы;
- средняя длина свободного пробега частицы;  - время между двумя столкновениями. Элементарные перемещения в твердом теле имеют одно и то же значение
- время между двумя столкновениями. Элементарные перемещения в твердом теле имеют одно и то же значение  . Тогда:
. Тогда: ()
() , ()
, () ()
() .
. ()
() 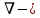 оператор градиента. В общем случае диффузия анизотропна и коэффициент диффузии D - тензор второго ранга – равен:
оператор градиента. В общем случае диффузия анизотропна и коэффициент диффузии D - тензор второго ранга – равен: ()
()
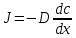 , а поток через вторую плоскость
, а поток через вторую плоскость 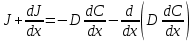 . Тогда разность потоков
. Тогда разность потоков  Но
Но  равно взятой с обратным знаком скорости изменения концентрации т.е.
равно взятой с обратным знаком скорости изменения концентрации т.е.  . Таким образом,
. Таким образом, ()
() ()
()  ()
() . С другой стороны
. С другой стороны