поурочные. Урок 6. Треугольника и трапеции

• Название: Треугольника и трапеции
• Анкор: поурочные
• Дата: 24.11.2022
• Размер: 75.83 Kb.
• Имя файла: Урок 6.docx
• Тип: Урок; #810917

Урок 6
ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА,
ТРЕУГОЛЬНИКА И ТРАПЕЦИИ

Цели: доказать теорему о площади трапеции; познакомить учащихся с методами решения задач по этой теме.

Ход урока

I. Проверка домашнего задания.

№ 469.

SАВС = AB ∙ CD, SАВС = 16 ∙ 11 = 88 (см2), SАВС = BC ∙ h, 88 = ∙ 22 ∙ h, h = 8 (cм).

№ 472.

SАВС = , так как . АС = , 168 = , ВС2 = , ВС2 = 24 · 24, ВС = 24см, АС = 14см.

№ 479 (а).

, , SАDE = = 2 (см2).

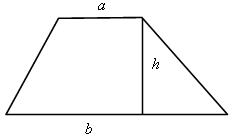
II. Объяснение нового материала.

Доказательство теоремы о площади трапеции можно предложить учащимся разобрать самостоятельно.

III. Закрепление изученного материала.

Решить задачу.

Дано: S = 18 см², а = 2 см, b = 7 см.

Найти: h.

Ответ: h = 4 cм.

№ 480 (в).

Решение

SАВСD = ∙ BC, SАВСD = ∙ 8, SАВСD = 72 (см2).

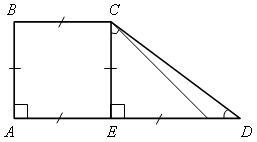
№ 481.

Решение

ВСD = 135°, ВСЕ = 90°, ЕСD = 45°, СDЕ = 45°. Имеем СDЕ – равнобедренный, то есть СЕ = ЕD. Четырехугольник АВСЕ – квадрат, поэтому АВ = СЕ = ВС = АЕ.

S_АВСD = ∙ AB = ∙ 6 = 36 (см²).

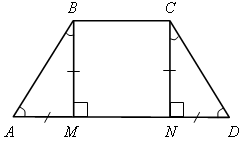
№ 482.

Решение

ВСD = 135°, NСL = 45°, NСD = СDN = 45° NС = ND = 1,4 см; МN = AN – MN = 3,4 – 1,4 =2 (см); МN = ВС.

S_АВСD = ∙ NC = ∙ 1,4 = 4,76 (см²).

IV. Итоги урока.

Sтрапеции =

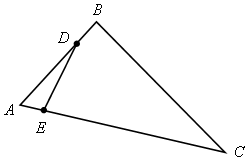
Домашнее задание: § 2, вопрос 7, с. 134; №№ 480 (8), 518 (а).

Для желающих.

В трапеции АВСD, АD – большее основание, D = 60°. Биссектрисы углов С и D пересекаются в точке 0, ОD = а, ВС = b, АD = с. Найдите площадь трапеции.

Решение

СDЕ – равносторонний, так как МСD = СDМ = = СМD = 60°. СМ = ОD, то есть ОD – высота МСD. В равностороннем треугольнике высоты равны.

S_АВСD = ∙ OD = ∙ a.