Лабораторная работа 0-1: обработка результатов физического эксперимента. В физическом практикуме
 Скачать 0.56 Mb.
|
1 2 Министерство Российской Федерации по связи и информатизации САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М. А. БОНЧ-БРУЕВИЧА А.Д. Андреев, Л.М. Черных  ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙВ ФИЗИЧЕСКОМ ПРАКТИКУМЕ Конспект лекции Санкт-Петербург 2009 УДК 530.1 Андреев А.Д., Черных Л.М. Физика.Обработка результатов измерений в физическом практикуме: Конспект лекции / СПб ГУТ.-СПб, 2009. Рекомендован к печати редакционно-издательским советом университета Содержит изложение методики обработки результатов измерений, получаемых во время практических занятий в учебной лаборатории. Предназначен для оказания помощи студентам технических специальностей всех форм обучения при подготовке к лаборатор-ным работам и при оформлении отчетов по ним. Ответственный редактор Рецензент © Андреев А.Д., Черных Л.М., 2009. © Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А.Бонч-Бруевича, 2009. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙВ ФИЗИЧЕСКОМ ПРАКТИКУМЕ Введение. Теоретические основы обработки результатов измерений в физическом эксперименте - предмет отдельного курса лекций. Ниже изложены основные понятия по обработке результатов прямых равноточных и косвенных измерений, как некоторый алгоритм действий, основанный на выводах теории погрешностей [1]. При любом измерении неизбежно возникают ошибки (погрешности измерений), приводящие к отклонению измеренного значения x от истинного значения  измеряемой величины X. Поэтому при записи результата измерений или вычислений принципиально важна оценка точности полученного числа. В физическом эксперименте результат представляется в виде:X = (54, 3  0, 2)  м  0,7.Такое представление означает, что истинное значение величиныX с вероятностью 70% находится в диапазоне от 54,1 м до 54,5 м на числовой оси.Цель настоящего пособия: научиться определять погрешность измерения. Иными словами, как, зная  (доверительная вероятность), рассчитывать абсолютную погрешность или ошибку измерений Δx ( 0,2 м), определяющую диапазон значений на числовой оси (доверительный интервал), в котором лежит ожидаемое истинное значение измеряемой величины.Вначале введём некоторые важные понятия и термины. Абсолютная погрешность сама по себе ничего не говорит о точности измерения. Например, если абсолютная погрешность измерения напряжения ΔU = 20 мВ, то нельзя сказать, точным ли было измерение. Если напряжение равнялось 40 мВ, то очевидно измерение грубое. Если же напряжение было равно 220 В, то измерение можно считать точным. Чтобы охарактеризовать точность измерения, вводят относительную погрешность:  .Если,  то измерение точное. Если это условие не выполняется, то измерение надо считать неточным.Для введения основных понятий и в качестве иллюстрации рассмот-рим простейшую лабораторную работу: «Определение ускорения сво-бодного падения при помощи математического маятника». Из известной формулы периода колебаний математического маятника получаем выражение для вычисления ускорения свободного падения:  . (1)Цель работы: измеряя длину нити маятника L и время одного полного колебания T, по формуле (1) определить ускорение свободного падения g. Измерения L и Т, сделанные при помощи приборов, называются прямыми измерениями. Ускорение свободного падения g рассчитывается по формуле (1). Такое измерение называется косвенным измерением. Формула, по которой после подстановки результатов прямых измерений получают результат косвенного измерения, называется рабочей формулой. В нашем примере это формула (1). Она даёт связь между результатом косвенного измерения g и результатами прямых измерений L и T. Рабочая формула является исходной при выводе формулы для расчета погрешности косвенного измерения (см. ниже). В нашей модельной работе, если делать измерения времени не для одного, а для Nполных колебаний маятника, рабочая формула имела бы другой вид:  , (2)где  - время N полных колебаний маятника.Ещё одно понятие - равноточные измерения. Равноточными называются измерения, выполненные в одинаковых условиях: неизменными должны оставаться объекты исследования, используемые приборы, условия и время проведения эксперимента. Обработка результатов прямых равноточных измерений. Погрешности прямых измерений, в зависимости от причин их вызывающих, делятся на случайные, систематические и промахи (грубые ошибки). Промах. Промахом называется грубая погрешность, возникшая из-за невнимательности, непреднамеренного отклонения от стандартных условий эксперимента. Обычно в серии равноточных измерений промахи отчетливо видны. Их следует исключить и не учитывать при обработке результатов измерений. Случайные ошибки. Под случайными ошибками понимают ошибки, связанные с неконтролируемыми изменениями условий равноточных опытов, приводящими к разбросу численных значений измеряемой величины. Если измеряемая величина может принимать непрерывные значения, то ее нельзя измерить абсолютно точно. В этом случае говорят, что результаты измерений носят случайный характер. Пусть  - результаты n прямых равноточных измерений величины X. В серии равноточных экспериментов без учета систематической погрешности (см. ниже) полученные значения X находятся в окрестности истинного значения на числовой оси. Отметим, что истинное значение может вообще не существовать. Во всяком случае, оно практически никогда не известно. Так, измеряя длину цилиндра, мы предполагаем, что это прямой цилиндр, с идеально параллельными друг другу торцами. Так как это может не соответствовать действительности, то об истинной длине цилиндра говорить не имеет смысла. Это же замечание относится к определению «истинной» длины нити, легко подвергающейся деформации растяжения. В дальнейшем будем предполагать, что истинное значение измеряемой величины существует. Как следует из теории погрешностей [1], за наиболее вероятное значение измеряемой величины X обычно принимают ее среднее арифметическое значение, вычисленное по результатам n равноточных измерений: 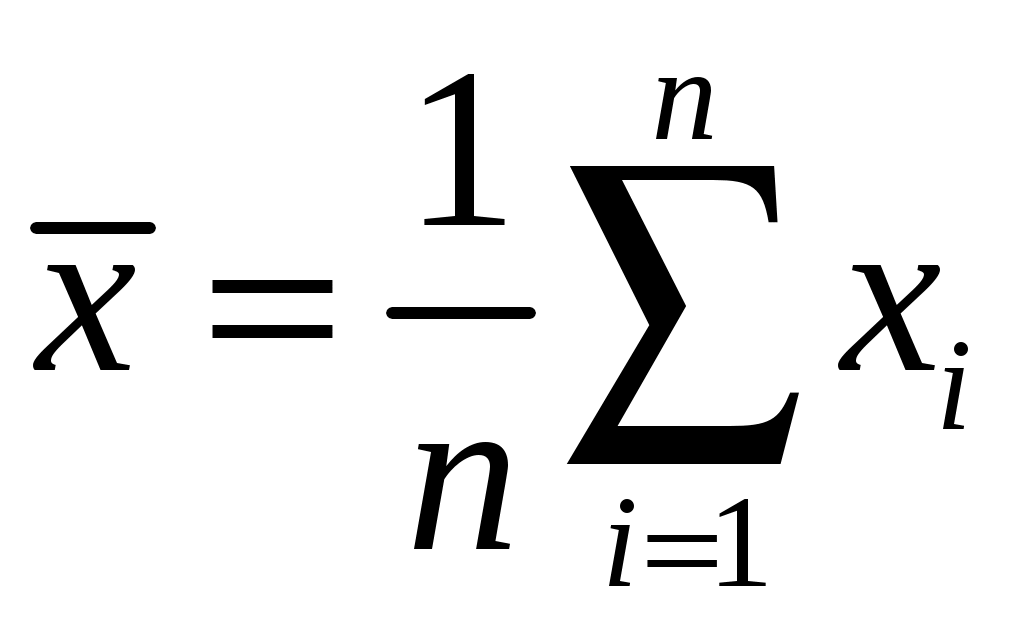 , (3) при этом n должно быть достаточно большим. Отклонения измеренных значений от среднего  носят случайный характер и подчиняются статистическим закономерностям. Как известно из опыта, для большого числа n равноточных измерений распределение случайных ошибок измерений  подчиняется нормальному или «гауссовскому» закону. Т.е. ошибки измерений могут принимать непре-рывный ряд значений; при большом числе равноточных измерений ошибки одинаковой величины, но противоположного знака встречаются одинаково часто; малые ошибки более вероятны, чем большие.Известно, что мерой осуществления случайного события А является его вероятность Р(А). Если в n однородных испытаниях событие А произошло k раз, то величина 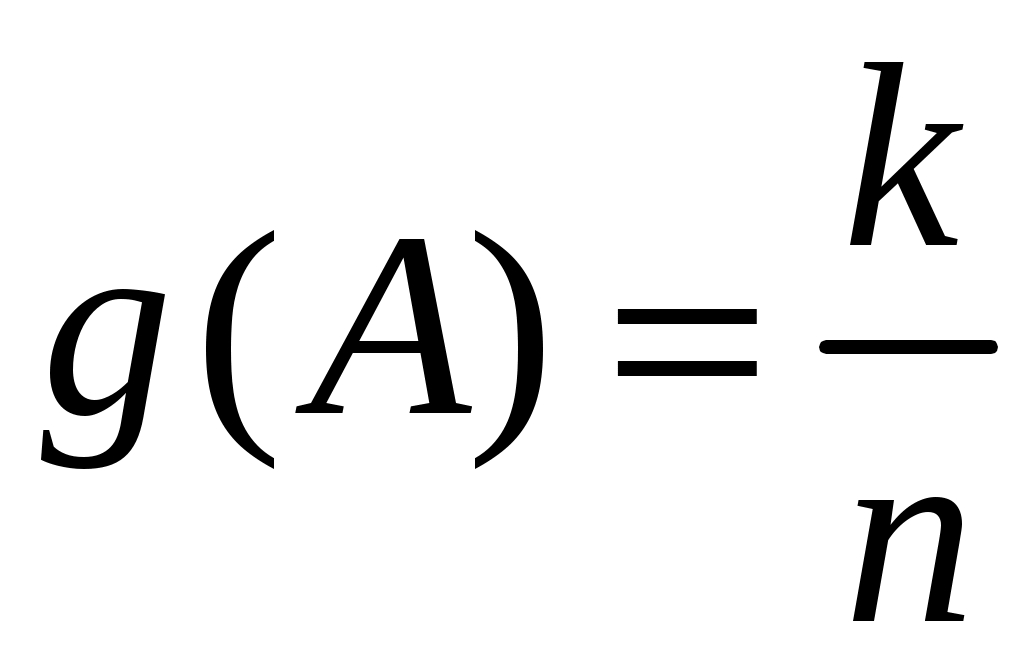 определяет относительную частоту появления этого события. 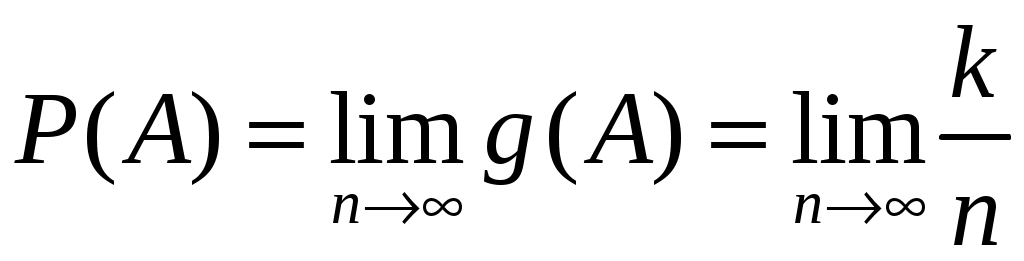Предел  при  равен вероятности события А: .Из определения вероятности следует, что  . Вероятность невозможного события равна нулю. Вероятность достоверного события равна единице.Обозначим за  - вероятность того, что истинное значение Х не выйдет за границы так называемого доверительного интервала  . Соответствующую этому доверительному интервалу вероятность называют доверительной вероятностью или надежностью. Ширина довери-тельного интервала, равная 2  , связана с доверительной вероятностью . Очевидно, что с увеличением ширины доверительного интервала растет ве-роятность, что истинное значение Х попадет в этот интервал.Задавая значение доверительной вероятности , рассчитываютслучайную погрешность  и определяют, таким образом, доверительный интервал  .Случайная погрешность определяется по формуле:  (4) называется средней квадратической погрешностью и вычисляется по формуле: 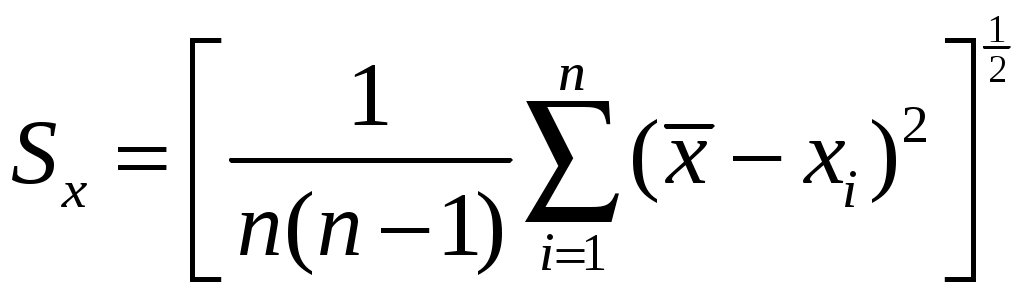; (5)величина  называется коэффициентом Стьюдента и определяется по таблице для заданных значений и n [1] . Табл. 1. Коэффициенты Стьюдента.
Из табл.1 видно, что для определенного значения n увеличение довери-тельной вероятности сопровождается увеличением , а, следовательно, согласно (4), увеличением , т.е. доверительный интервал становится шире. Из табл.1 также видно, что при  коэффициент Стьюдента слабо зависит от n. Обычно, число измерений  ,  0,7 и =1,2 . 1 2 | ||||||||||||||||||||||||||||||||