задачи по физике. Вариант 9 24
 Скачать 112.86 Kb. Скачать 112.86 Kb.
|
|
Вариант № 9 1.24 С покоящимся шаром массой m = 4 кг сталкивается такой же шар, движущийся со скоростью υ = 1 м/с. Вычислить работу, совершенную вследствие деформации при прямом центральном неупругом ударе.  Дано: Решение: Дано: Решение:    (m1+m2)*V m2V2 m1V1 m1=m2=4 кг        V1=1 м/с V1=1 м/с V2=0 м/с  Неупругий удар По закону сохранения импульса: Неупругий удар По закону сохранения импульса:А-? m1V1+m2V2=(m1+m2)*V mV1+m*0=(m+m)*V  mV1=2mV V= mV1=2mV V= = = =0,5 м/с =0,5 м/сA= ΔEk=Ek1-Ek2= 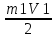 - - 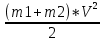 =0,5 Дж =0,5 ДжОтвет: А=0,5 Дж 1.34 Стержень вращается вокруг оси, проходящей через его середину согласно уравнению 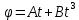 , где А =2 рад/с; В =0,2 рад/с. Определить вращающий момент М, действующий на стержень в момент времени t = 2 с, если момент инерции стержня I = 0,048 кг⋅м. , где А =2 рад/с; В =0,2 рад/с. Определить вращающий момент М, действующий на стержень в момент времени t = 2 с, если момент инерции стержня I = 0,048 кг⋅м. Дано: Решение: Дано: Решение:φ=At+B 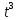 Из 2-го закона Ньютона, применяемого к Из 2-го закона Ньютона, применяемого к A=2 рад/с вращающимся телам находим: В=0,2 рад/с М= ε*J, где М – вращающий момент, ε - угловое t= 2 с ускорение, J- момент инерции стержня.   J=0,048 кг/ J=0,048 кг/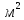 ω= ω= ω(t)= ω(t)=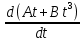 =A+3B =A+3B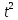  М-? ε= М-? ε=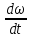 ε(t)= ε(t)= =6Bt=6*0,2*2=2,4 рад/ =6Bt=6*0,2*2=2,4 рад/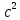 М= ε*J=2,4*0,048=0,1152 Нм Ответ: М=0,1152 Нм 2.29 Определить, какое количество теплоты необходимо сообщить аргону  массой т = 400 г, чтобы нагреть его на ΔТ = 100 К: а) при постоянном объеме; б) при постоянном давлении. массой т = 400 г, чтобы нагреть его на ΔТ = 100 К: а) при постоянном объеме; б) при постоянном давлении. Дано: m=400 г =0,4 кг ΔT=100 K M(Ar)=0,04 кг/моль А) V=const  B) P=const B) P=constA) Q1-? B) Q2-? Решение: А) Количество теплоты, необходимое для нагревания газа на ΔT при постоянном объеме: Q1=V*Cv* ΔT= 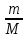 * * 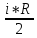 * ΔT, где Cv= * ΔT, где Cv=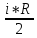 – молярная теплоемкость газа при постоянном объеме. – молярная теплоемкость газа при постоянном объеме.R=8,31 Дж/(моль*К) – универсальная газовая постоянная   Аргон – одноатомный газ i=3 степени свободы Аргон – одноатомный газ i=3 степени свободы Q1=  * * 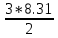 * 100=12465=1.2465 * * 100=12465=1.2465 *  ≈1.25 кДж ≈1.25 кДжВ) Количество теплоты, необходимое для нагревания на ΔT при постоянном давлении: Q2=V*Cp *ΔT= 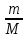 * * 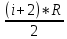 * ΔT, где Cp- молярная теплоемкость при постоянном давлении * ΔT, где Cp- молярная теплоемкость при постоянном давленииQ2=  * *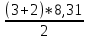 * 100=20775=2,0775 * * 100=20775=2,0775 *  ≈2,08 * ≈2,08 *  ≈20,8кДж ≈20,8кДжОтвет: Q1=1,25 кДж; Q2=20,8 кДж 2.59 Совершая цикл Карно, газ получил от нагревателя теплоту Q1 = 500 Дж и совершил работу А = 100 Дж. Температура нагревателя T1 = 400 К. Определить температуру Т2 охладителя.  Дано: Решение: Дано: Решение:Q1=500Дж КПД тепловой машины равен отношению производимой А=100 Дж работы к количеству тепла, полученному от нагревателя:  Т1=400 К η= Т1=400 К η=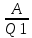 Т2-? Также η= 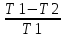 =1- =1- , где Т1 – температура нагревателя, , где Т1 – температура нагревателя,  Т2 – температура охладителя Т2 – температура охладителя Т2=Т1*(1- η)=Т1*(1- 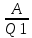 )=400*(1- )=400*(1-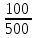 )=320 К )=320 КОтвет: Т2=320 К 3.15 Поверхностная плотность заряда σ бесконечно протяженной плоскости равна 400 мкКл/м. К плоскости на нити подвешен заряженный шарик массой m = 10 г. Определить заряд Q шарика, если нить образует с плоскостью угол α = 30°.  Дано: Дано: σ=400 мкКл/ 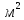 =4* =4*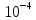 Кл/ Кл/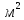   m=10 г = m=10 г =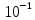 кг кгq-?        Y σ>0    T T                   X α E F   mg mgНапряженность поля бесконечной равномерно заряженной плоскости: Е= 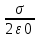 , где σ – поверхностная плотность заряда плоскости; ε0=8,85 * , где σ – поверхностная плотность заряда плоскости; ε0=8,85 * 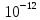 ф/м – электрическая постоянная. ф/м – электрическая постоянная. На шарик действуют 3 силы: На шарик действуют 3 силы:- сила со стороны электрического поля плоскости F: F=qE= 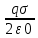 -сила тяжести mg, где m – масса шарика, g=9,81 м/ 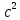 – ускорение свободного падения – ускорение свободного падения- сила натяжения нити Т.    По 2-му закону Ньютона для шарика, находящегося в равновесии: По 2-му закону Ньютона для шарика, находящегося в равновесии:F + mg + T=0 В проекции на оси X и Y: 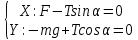 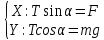   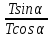 = =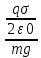 tg α= tg α=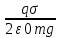 = =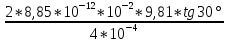 ≈2,5* ≈2,5* Кл=2,5 нКл Кл=2,5 нКлОтвет: q=2,5 нКл 3.56 Внешняя цепь источника тока потребляет мощность Р = 0,75 Вт. Определить силу тока в цепи, если ЭДС источника тока ε = 2 В и внутреннее сопротивление r = 1 Ом.  Дано: Решение: Дано: Решение:Р=0,75 Вт P=U*I= 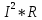 Ε=2 В I= 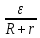 , тогда P=( , тогда P=(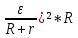  r=1 Ом R= r=1 Ом R=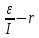 , тогда P= , тогда P= –r)= ε*I - –r)= ε*I - 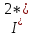 r rI - ? 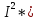 r - I* ε + P=0 r - I* ε + P=01* 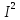 – 2*I + 0,75=0 – 2*I + 0,75=0По теореме Виета находим корни I1=0,5; I2=1,5 Ответ: I1=0,5 А; I2=1,5А |
