Высшая Математика. Задания. Вычисление определителей, ранга матриц.
 Скачать 148.51 Kb. Скачать 148.51 Kb.
|
|
Практическая работа № 1 Тема: «Вычисление определителей, ранга матриц.» Цель работы: научиться выполнять действия над матрицами, вычислять определители. Методические указания по выполнению работы: 1. Ознакомиться с теоретическим материалом по практической работе. 2. Рассмотрите образцы решения задач по теме. 3.Выполнить предложенное задание согласно варианту по списку группы. Краткие теоретические и учебно-методические материалы по теме практической работы Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде  или сокращенно: 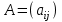 , где , где 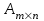 . Числа . Числа  , составляющие матрицу, называются ее элементами. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается , составляющие матрицу, называются ее элементами. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается Действия над матрицами Сложение Операция сложения матриц вводится только для матриц одинаковых размеров. Суммой двух матриц Умножение вектора на число Произведением матрицы Произведение матриц Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы 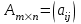 на матрицу на матрицу 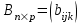 называется матрица называется матрица  такая, что такая, что 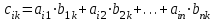 , где , где  т. е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В. Тогда произведение 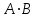 не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение 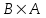 , которое считают следующим образом: , которое считают следующим образом: 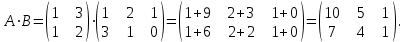 Умножение матриц обладает следующими свойствами: 1. 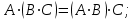 3. 3. 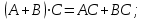 2.  4. 4. 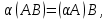 Определитель матрицы Квадратной матрице А порядка n можно сопоставить число det А (или  , или , или 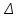 ), называемое ее определителем, следующим образом: ), называемое ее определителем, следующим образом:1. 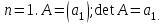 2. 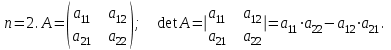 3.   Свойства определителей Если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю. Свойство1. («Элементарные преобразования определителей»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число. Минором некоторого элемента  определителя n-го порядка называется определитель n - 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается определителя n-го порядка называется определитель n - 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается  . Так если: . Так если: то то 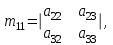 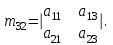 Алгебраическим дополнением элемента  определителя называется его минор, взятый со знаком «плюс», если сумма определителя называется его минор, взятый со знаком «плюс», если сумма 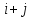 четное число, и со знаком «минус», если эта сумма нечетная. Обозначается четное число, и со знаком «минус», если эта сумма нечетная. Обозначается  . .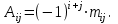 Свойство 2. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения. В случае определителей 3-го порядка свойство 7 означает, что 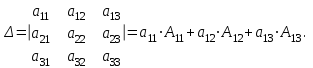 Квадратная матрица А называется невырожденной, если определитель ∆ = det A≠0. В противном случае (∆ = 0) матрица А называется вырожденной. Союзная и обратная матрицы Матрицей союзной к матрице А называется матрица: A*=  , ,где А где Е – единичная матрица того же порядка, что и матрица А. Пусть А – невырожденная матрица A=  , и det A≠0. , и det A≠0.Составим союзную матрицу A*=  Тогда A  , т.е. A , т.е. A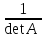 · · . .Отметим свойства обратной матрицы: det(A 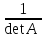 ; ;(A·B) (A Пример по выполнению практической работы Пример 1. 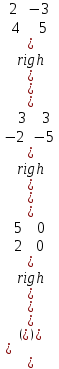 Пример 2. Пример 3. 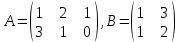 . . Пример 4. Найти определитель матрицы  . .Решение: 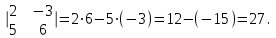 Пример 5. Вычислить определитель  Ответ: =4. Пример 7. Найти А 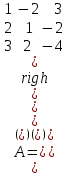 Решение:  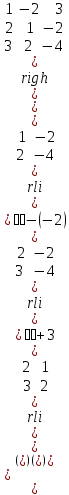 Составим союзную матрицу. Для этого вычислим алгебраические дополнения: 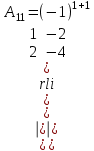 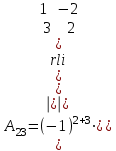  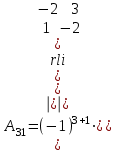 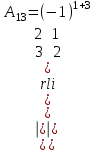 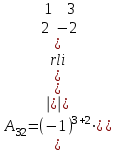 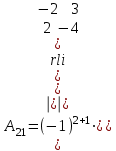 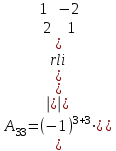  Союзная матрица будет следующей: 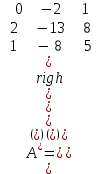 . Вычислим обратную матрицу: . Вычислим обратную матрицу: 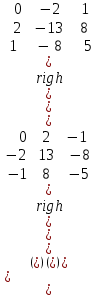 Проверкой  убеждаемся, что обратная матрица найдена верно. убеждаемся, что обратная матрица найдена верно.Задания для практического занятия: Даны матрицы А и В. Найти: A+ B, A-B C=2A-3B AB; BA det A; det B A‾ ¹, B‾ ¹. Проверить правильность их нахождения умножением Вариант 1 Вариант 2 A=  ; B = ; B = ; A = ; A =Вариант 3 Вариант 4 A =  ; B = ; B = ; A = ; A = ; B = ; B =Практическая работа № 2 «Решение систем линейных уравнений методом обратных матриц» Цель работы: научиться решать системы линейных уравнений методом обратной матрицы. Методические указания по выполнению работы: 1. Ознакомиться с теоретическим материалом по практической работе. 2. Рассмотрите образцы решения задач по теме. 3.Выполнить предложенное задание согласно варианту по списку группы. Краткие теоретические и учебно-методические материалы по теме практической работы Система линейных уравнений. Основные понятия Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида  (1) (1)где числа здесь А – матрица коэффициентов системы, называемая основной матрицей:   вектор - столбец из неизвестных вектор - столбец из неизвестных  вектор - столбец из свободных членов вектор - столбец из свободных членов Расширенной матрицей системы называется матрица  (4) (4)Решением системы называется Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеетни одного решения. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему – это значит выяснить, совместна она или не совместна и если система совместна, значит найти ее общее значение. Две системы называются эквивалентными (равносильными), если они имеют одно и то же решение. Эквивалентные системы чаще всего получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы. Решение систем методом обратных матриц Пусть дана система п линейных уравнений с п неизвестными:  (5) (5)или в матричной форме  называется главным определителем системы.Если определитель системы отличен от нуля, то система называется невырожденной. Найдем решение данной системы уравнений в случае Поскольку Отыскание решения системы по формуле (1) называют методом обратных матриц решения системы. Пример по выполнению практической работы Пример 1. Решить систему уравнений методом обратных матриц:  Решение:  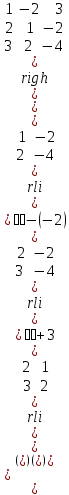 Составим союзную матрицу. Для этого вычислим алгебраические дополнения: 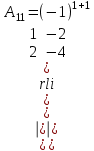 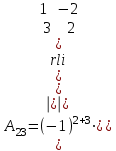  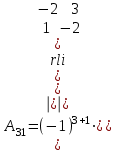 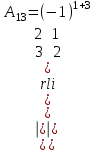 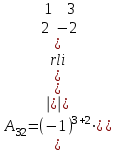 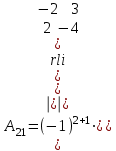 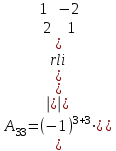  Союзная матрица будет следующей: 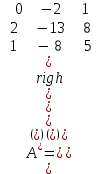 . . Вычислим обратную матрицу:  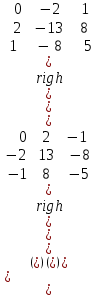 Найдем решение системы по формуле (6):  . .Итак, решением системы будет тройка чисел (1; 2; -1) Задания для практического занятия: Вариант 1 Методом обратных матриц найти решение системы: а)  б) б) 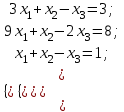 в) в)  Вариант 2 Методом обратных матриц найти решение системы: а)  в) в) 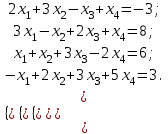 Вариант 3 1. Методом обратных матриц найти решение системы: а) 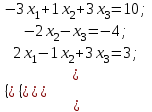 в) в) 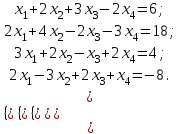 Вариант 4 1. Методом обратных матриц найти решение системы: а) 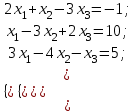 б) б)  в) в) 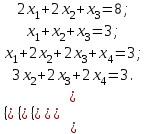 |
