отчет по практике. Лабораторная 1_Алгараева-исправленная работа. Выявление аномалий в корпоративных данных с помощью закона бенфорда
 Скачать 169 Kb. Скачать 169 Kb.
|
КАФЕДРА ФИНАНСОВОГО МОНИТОРИНГА ЛАБОРАТОРНАЯ РАБОТА ПО ДИСЦИПЛИНЕ «ЭКОНОМИЧЕСКАЯ БЕЗОПАСНОСТЬ» НА ТЕМУ «ВЫЯВЛЕНИЕ АНОМАЛИЙ В КОРПОРАТИВНЫХ ДАННЫХ С ПОМОЩЬЮ ЗАКОНА БЕНФОРДА»
Москва, 2022 г. ОглавлениеВведение 3 Первичная обработка данных 4 Проведение базовых тестов 4 Тест первой цифры 4 Тест второй цифры 6 Тест первого порядка 7 Проведение продвинутых тестов 8 Тест суммирования для первой пары цифр 9 Тест второго порядка 9 Тест мантисс 10 Проведение связанных тестов 11 Тест дублирования сумм 11 Тест последних двух цифр 12 Оценка коэффициента искажения 13 Анализ полученных результатов 13 Заключение 16 Список использованной литературы 17 ВведениеСегодня развитие бизнес-процессов происходит благодаря современным устройствам. В результате это приводит ко многим проблемам. Одним из них является фальсификация финансовых данных, которая распространена в сфере экономики и финансов. Для специалистов, работающих в этой сфере, необходимо иметь определенный инструмент для выявления фальсифицированных данных. Такой инструмент был изобретен в 1938 году. Автором этого закона является Фрэнк Бенфорд. Этот инструмент широко используется с 1990-х годов. В рамках данной лабораторной работы необходимо изучить и подтвердить на практике методику выявления в выборочных наборах финансовой информации нестандартных элементов, свидетельствующих о ее возможном искажении, с использованием основных методов, основанных на законе Бенфорда, а также усовершенствованных и соответствующие тесты. Анализ банковских выписок, отображаемых в Excel, позволяет определить и оценить вероятность ручного вмешательства в выписки и, как следствие, вероятность манипулирования данными. Задачами лабораторной работы №1 являются: Первичная обработка данных Проведение базовых тестов Проведение продвинутых тестов Проведение связанных тестов Анализ полученных результатов Первичная обработка данных Для данного анализа был использован большой объем данных. Количество строк «Сумма» составляет 127 886. Из них 947 записей не содержат информации в поле «Сумма». Оставшиеся 126 912 записи содержат суммы в пределах от -30 082 228 до 500 000 000 рублей. Довольно большой набор данных, также все данные представлены в виде чисел, единицы измерения (рубли). В наборе данных больше мелких наблюдений чем крупных. Величина выборки состоят из несколько порядков. Имеются числа малых порядков, но они не будут фальсифицировать наш конечный результат. Таким образом, можем говорить, что для анализа данных, ряд условий выполнен, следовательно можем приступить к выполнению базовых, продвинутых и связанных тестов. Проведение базовых тестов Широко распространенными являются базовые тесты, а именно тест первой цифры, тест второй цифры и тест первых двух цифр. Для первой цифры и второй цифры набор данных анализируется на частоту появления различных цифр. Для первой цифры в числе от 1 до 9. Для второй цифры в числе от 0 до 9. Для первой и второй цифры в числе от 10 до 99. Проведение базовых тестов на основе положительных сумм позволяет выявить вероятности завышения показателей. Тест первой цифры Первым из базовых тестов является анализ первой цифры всех сумм. Для выполнения данного теста из строки «Сумма» были отобраны цифры больше 1. Значения, которые меньше 0 не может в данном тесте, следовательно их убираем. Таким образом, останется 123 598 операции (N). Полученное распределение частоты использования каждой цифры в качестве первой цифры представлено на рисунке 1. 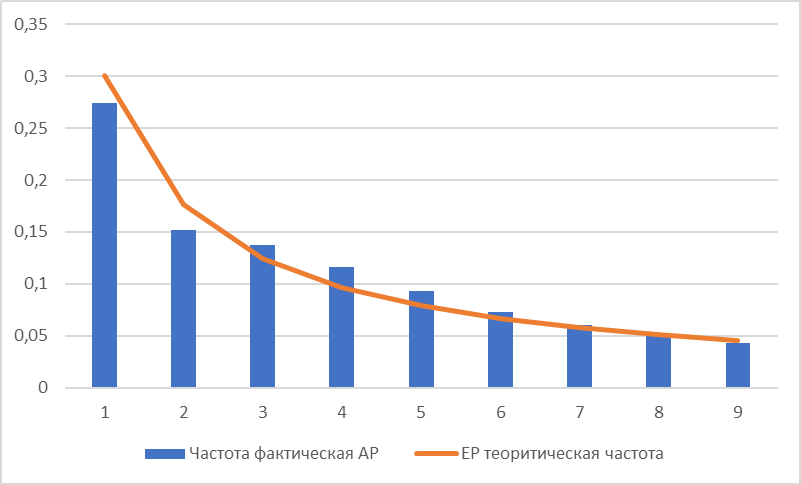 Рисунок 1 – Распределение теоретической и фактической частоты для первой цифры Далее были рассчитаны такие показатели, как Z-статистика для каждой цифры, Xи-квадрат статистика по выборке и MAD. Полученные результаты представлены в таблице 1. Таблица 1 – Результаты теста первой цифры
Продолжение таблицы 1
Тест второй цифры Для данного теста были отобраны из строки «Сумма» операции, суммы по которым больше или равны 10. Сумма операций больше и равно 10 составляет 127 198. Отличие данного теста от предыдущего в частоте (от 0 до 9). Соотношение фактического и ожидаемого распределения приведено на рисунке 2. Рисунок 2 – Распределение теоретической и фактической частоты для первой цифры 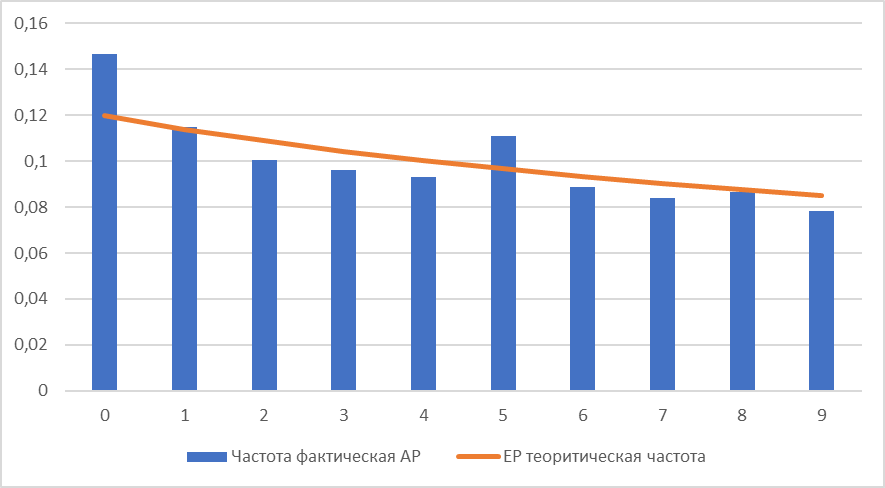 Далее были рассчитаны такие показатели, как Z-статистика для каждой цифры, Xи-квадрат статистика по выборке и MAD по выборке. Полученные результаты представлены в таблице 2. Таблица 2 – Результаты теста второй цифры
Тест первого порядка Для данного теста также используются операции строго больше или равно 10. Гистограмма приведена на рисунке 3. 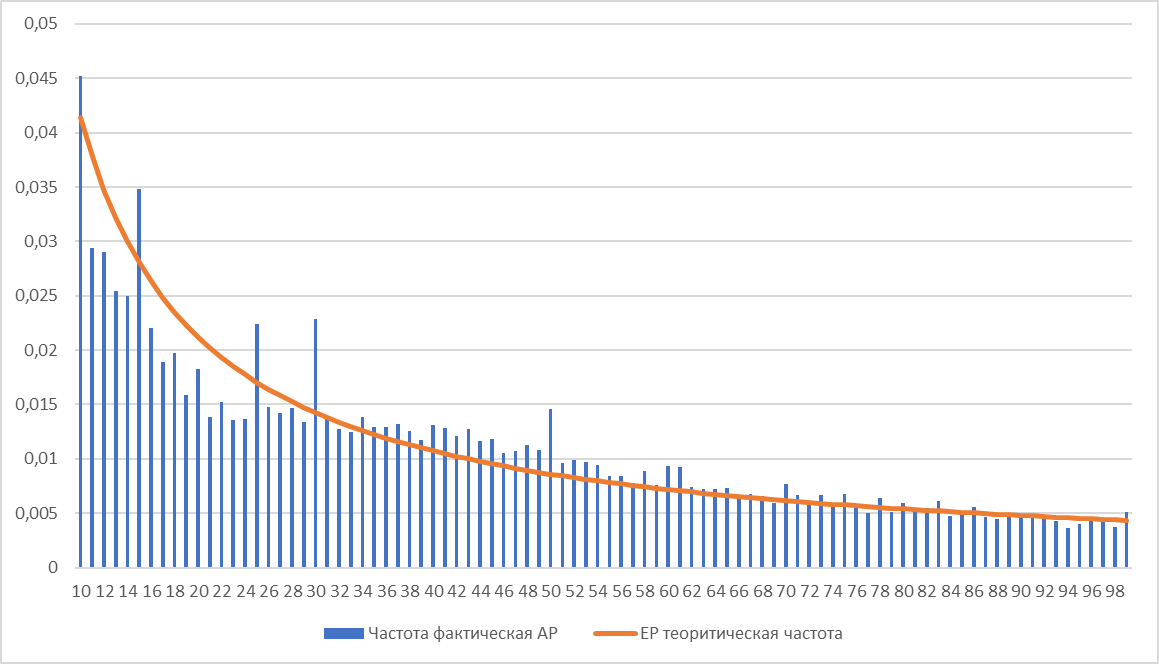 Рисунок 3 – Распределение теоретической и фактической частоты для первой пары цифр Для оценки данного теста были рассчитаны Z-статистика с уровнем значимости 5%,хи квадрат, MAD. Из 90 пар согласно по Z статистике, частоты 27 пар соответствуют распределению Бенфорда. Из 67/4 пар, которые обладают наибольшими Z-статистики будут приведены в таблице 3. Таблица 3 - Результаты теста первой пары цифр
Проведение продвинутых тестов Исходя из базовых тестов можно утверждать, что распределение данных не соответствует распределению Бенфорда. Поэтому для продолжения анализа будут применены продвинутые тесты, которые применимы к почти любому набору данных. Все базовые тесты проводились на основании данных по положительным суммам, продвинутые же тесты будут проведены на всех суммах, взятых по модулю. Тест суммирования для первой пары цифр По результатам теста более чем на 1% от ожидаемой частоты отклоняются частоты сумм:11-13,15–17,20,23,28,30,34,40,80. Общая сумма по записям с предположительно повторяющимися суммами составляет более 15млрд рублей. График распределения частот представлен на рисунке. 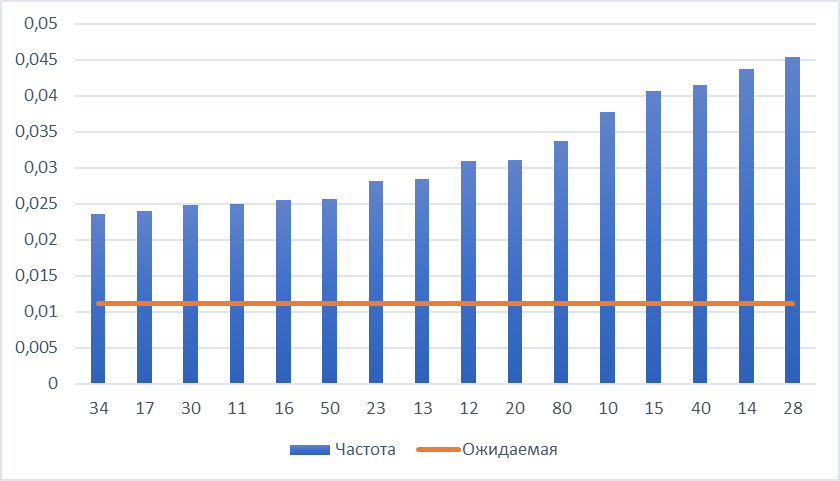 Рисунок 4 – Распределение частот сумм с наибольшим отклонением Рисунок 4 – Распределение частот сумм с наибольшим отклонениемТест второго порядка Для проведения теста второго порядка необходимо упорядочить данные по полю «Сумма» по возрастанию и посчитать разности между соседними суммами, умножить получившиеся значения на 10 и отобрать первые 2 цифры. Была построена гистограмма частот (от 10 до 99). Полученный результат представлен на рисунке 5. 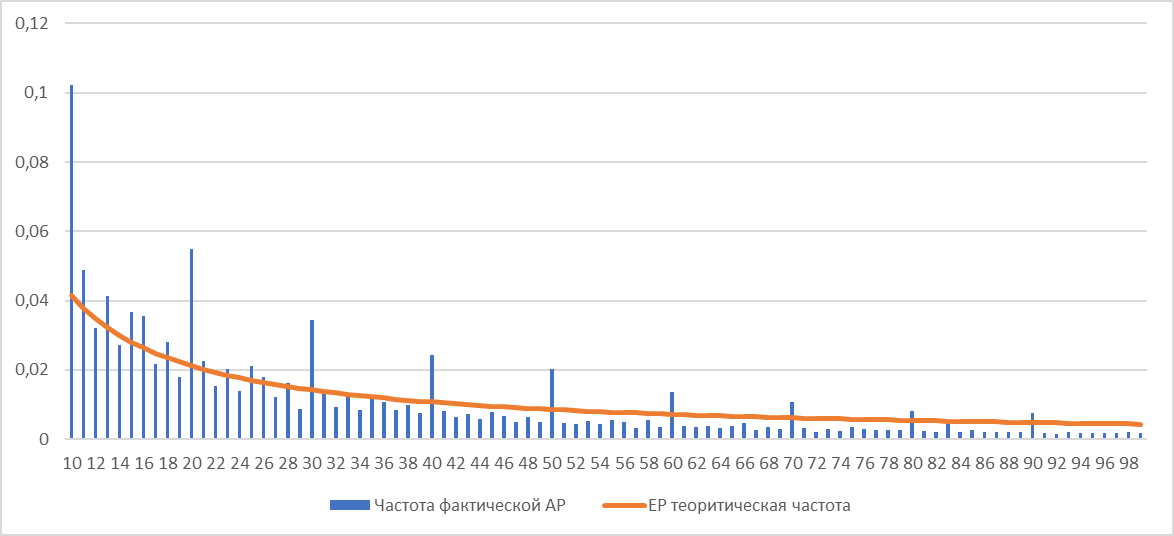 Рисунок 5 – Распределение теоретической и фактической частоты для первой пары цифр Рисунок 5 – Распределение теоретической и фактической частоты для первой пары цифрПосле проведения теста второго порядка были рассчитаны статистические показатели исходя из которых видно, что большая часть пар цифр не соответствует распределению Бенфорда согласно z-статистике. В таблице 4 будут приведены значения статистики, которые наиболее отклоняются от критического значения. Таблица 4 - Результаты теста второго порядка
Тест мантисс Рассчитанные в ходе теста логарифмы мантисса при нанесении на координатную плоскость образовали график, приведенный на рисунке 6 – окружность с координатами центра (-0,01162; -0,008709). С использованием координат центра окружности рассчитывается p-value. Он равен 1, что значительно превышает критическое значение равное 0,05, следовательно гипотеза о соответствии распределения распределению Бенфорда отвергается. 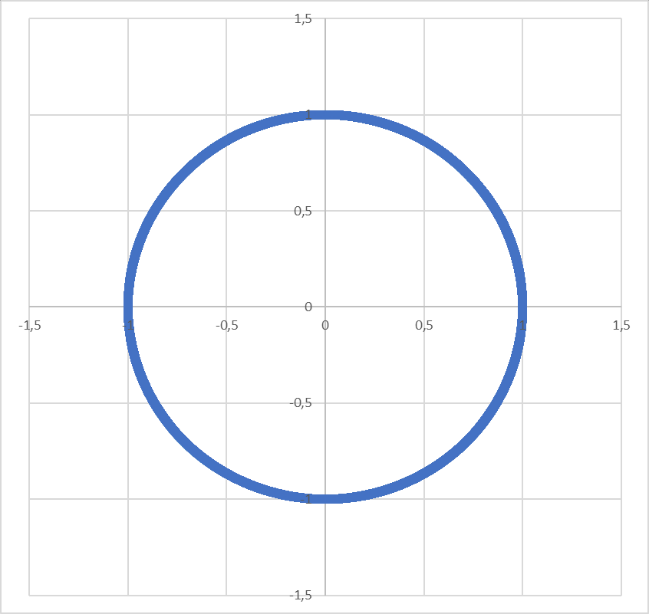 Рисунок 6 – распределение мантисс логарифмов Рисунок 6 – распределение мантисс логарифмовПроведение связанных тестов Связанные тесты основаны не на законе Бенфорда, а на иных особенностях распределения цифр и чисел. Связанные тесты могут указывать на ошибки, выдуманные числа или чрезмерное округление. Тест дублирования сумм После проведения расчета получим, что уникальных сумм в выгрузке из 1С 50981, но некоторые из них повторяются более 200 раз. Гистограмма с самыми часто повторяющимися уникальными значениями, а именно больше 200 повторений приведен на рисунке 7. 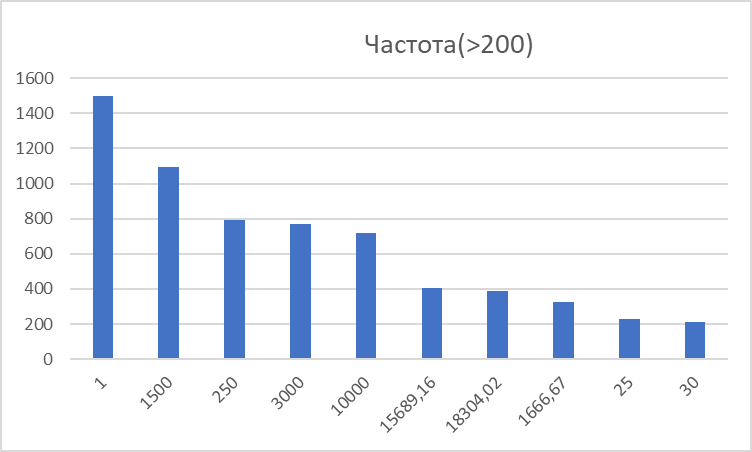 Рисунок 7 – Топ сумм по частоте повторения Тест последних двух цифр В рамках теста можно выявить аномальные значения в правой части числе. Например: частота чисел оканчивающихся на 00 довольно сильно расходится с ожидаемой частотой. Соотношение фактической АР и ожидаемой ЕР представлено на рисунке 11. 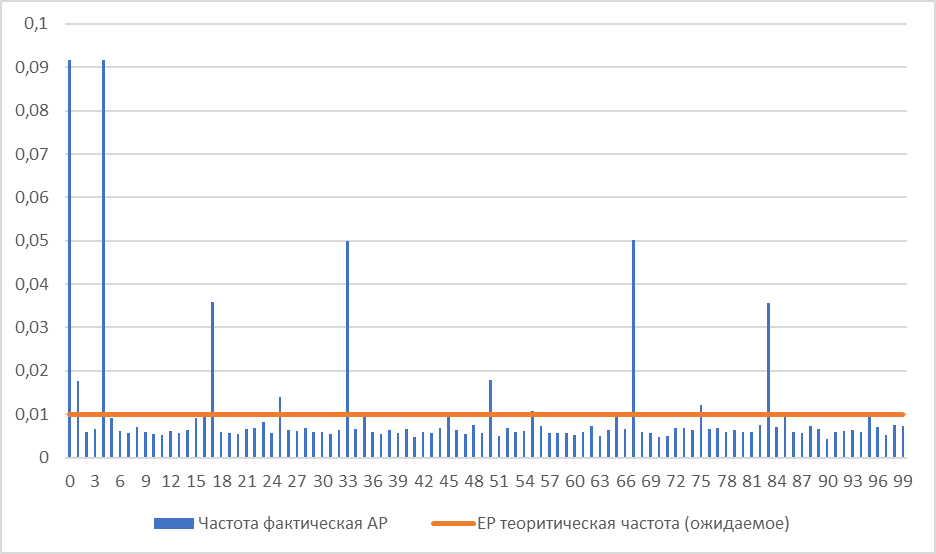 Рисунок 8 – Соотношение фактической и теоретической частоты распределения двух последних цифр Для интерпретации полученных результатов были рассчитаны значения статистических характеристик, приведенные в таблице 5. В таблицу вынесены только те последние цифры, z-статистики по которым являются максимальными. Таблица 5 – Значения z-статистики, статистики хи-квадрат и MAD для теста
Оценка коэффициента искажения Для определения данных завышенными или заниженными, а также степень искажения, используется данный тест. В рамках данного теста были получены следующие результаты, приведенные в таблице 6. Таблица 6 – Результаты теста
Анализ полученных результатов Все перечисленные тесты, а именно: базовые тесты(тест первой цифры, тест второй цифры, тест первого порядка), продвинутые тесты(тест второго порядка, тест суммирования, тест мантисс), связанные тесты(тест последних двух цифр, тест дублирования сумм, оценка коэффициента искажения) использовались для определения искажения в операциях и для выявления подозрительных операций а также для оценки манипулирования отчетностью. По результатам теста первой цифры можно говорить о том, что распределение Бенфорда выполняется только для цифры 8, так как его Z-статистика составляет 0,81>1.96. Для остальных цифр распределение Бенфорда не выполняется. Наибольшими, Z-статистиками обладают цифры 1,2,3,4,5,6.Это значит количество операций, суммы которых начинаются на данные цифры, сильно превышают ожидаемое количество. По результатам теста второй цифры также можно говорить о том, что распределение Бенфорда выполняется только для цифры 1, 8. Для остальных цифр распределение Бенфорда не выполняется. В данном тесте с наибольшими значениями z-статистики являются цифры 0, 2,5. Конечный базовый тест – тест по первой паре цифр, показал, что распределение не выполняется для цифр: 28, 31-33, 57, 59, 62, 63, 66-69, 74, 76, 79 ,81, 82, 84, 85, 87, 89, 90-92, 96, 97. Также можно заметить, что подозрительными операциями является цифры, которые были выявлены в предыдущих тестах. Эти операции, начинающиеся на 32(первая цифра на 2), на 62 (первая цифра 6, вторая цифра 2). Если проанализировать суммы, которые начинаются на 62. Можно прийти к выводу, что зачет аванса поставщику, НДС по предоплате, реализация услуг на одинаковую сумму, на сумму 6223 выглядит подозрительным. Посмотрим еще одну сумму, начинающиеся на 10. Реализация услуг на 10213 рублей в один день и без дополнительных документов к реализации. Таких операции более 50. Переходя к суммам, начинающимся на 32, заметим, что содержание подозрительных операций повторяется это большой объем списание с расчетного счета, и регламентная операция РОО. Из необычных операции, можем выделить комиссионные на сумму 10р, каждый день в течение месяца. В тесте суммирования подозрительными были выделены операции, начинающиеся на 40, 80. Для сумм начинающихся на 40 следует отметить операцию на счет-фактуру выданный. А также оплату страхования в одну и ту же компанию на одинаковую сумму 40636,8 рублей. Исходя из теста второго порядка наибольшие Z-статистики были получены у 10,20,30. Наиболее частыми суммами являются: 3000,30. Если сказать про сумму 3000, то это Лизинговые платежи по договору, а сумма 30 рубли комиссия за внутрегеиональный/межрегиональный перевод. Странным является то, что комиссия оплачивалось несколько раз на дату 12.04.2022. Возможно организация осуществляет денежные переводы по субъектам РФ, а от основной суммы удерживается комиссия в виде %. Наибольшей частотой, согласно тесту, обладают операции оканчивающиеся на 00, что говорит о чрезмерном округлении в отчетности. По тесту последних двух цифр, наиболее отличающимися Z-статистикой является: 17, 33, 64, 83. Суммы начинающиеся: от 17 равно 2353, от 33 равно 1554, от 64 равно 904, от 83 равно 762 операции. В конце хотелось бы отметить, что все организации, которые осуществляют свою деятельность с денежными средствами или иным имуществом, обязаны применять Федеральный Закон №115. Согласно статье 4 Федерального закона от 07.08.2001 N 115-ФЗ (ред. от 14.07.2022) "О противодействии легализации (отмыванию) доходов, полученных преступным путем, и финансированию терроризма" все организации должны применять меры на противодействие легализации (отмыванию) доходов, полученных преступным путем, финансированию терроризма и финансированию распространения оружия массового уничтожения. К таким мерам относятся: внутренний контроль и обязательный контроль. Внутренний контроль необходим для недопущения отклонений в отчетности, для принятия мер по предупреждению и устранению нарушений. Исходя из 9 тестов были выявлены множество подозрительных операций, которые могут показаться подозрительными внутреннему контролеру. Возможно, в организации недостаточная автоматизация ведения учета, что приводит к частым корректировкам сумм. Возможно, отсутствуют внимательность специалистов, что приводит к нескольким проведениям операций по одному и тому же счету, и на одну и ту же сумму. Также по тесту искажения коэффициента выявлена, что значения выборки завышена на 3,98%. Это завышение является несущественной, так как Z-статистика показал 0,16. Таким образом, Z-статистика меньше критического значения 1,96, что свидетельствует о том искажение не существенное. Следовательно, данное искажение не влияет на мнение пользователей этой выборки, о ее достоверности. Заключение В процессе применения закона в Бенфорда мы вновь убедились в их эффективности и удобстве. Однако, в ходе этих 9 тестов мы не можем точно сказать, что в компании отсутствует внутренний контроль и фальсификация данных, можно лишь сказать, что вероятность есть. В ходе проведенных тестов было установлено, что базовые тесты недостаточно для анализа выявления мошеннических схем. Для более подробного анализа необходимо использовать все 9 тестов. Подводя итог, мы можем сказать, в компании недостаточно развита система внутреннего контроля. Возможно такие значительные операции недостаточно контролируется ответственными лицами, отвечающими за корпоративные управления. Также нехватка процедур оценки риска организации, такие как неспособность руководства выявить риск существенного искажения, также исправления ранее выпущенной финансовой отчетности, отражающее существенного искажения по причине ошибки или же недобросовестных действий. А также неспособность главного бухгалтера за составлением отчетности. Все это в конечном счете приводится к мошенническим схемам, к отмыванию денег или же к другим видам преступления. Для предотвращения подобных досадных ситуаций необходимо усилить систему внутреннего контроля и проводить более масштабные проверки. Список использованной литературы Нормативные правовые акты Федеральный закон от 07.08.2001 N 115-ФЗ (ред. от 16.04.2022) «О противодействии легализации (отмыванию) доходов, полученных преступным путем, и финансированию терроризма» // КонсультантПлюс – компьютерная нормативно-справочная система. Научная литература Nigrini, M. J. Benford’s law: applications for forensic accounting, auditing and fraud detection. — Hoboken, New Jersey: John Wiley & Sons. — 2012. — С. 320. Интернет-источники Закон Бенфорда: как выявить обман и мошенничество с помощью математики | Научпоп. Наука для всех | Дзен (dzen.ru) |
