Тесты. Тест_1_2. Вопрос дискретен или непрерывен по частоте спектр произвольного дискретного сигнала Варианты ответов

• Название: Вопрос дискретен или непрерывен по частоте спектр произвольного дискретного сигнала Варианты ответов
• Анкор: Тесты
• Дата: 08.04.2022
• Размер: 95.5 Kb.
• Имя файла: Тест_1_2.doc
• Тип: Документы; #452781

ТЕСТ № 1 Студент группы З-БА-ИТСС-18 Решетников Игорь Владимирович

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

ВОПРОС 1. Дискретен или непрерывен по частоте спектр произвольного дискретного сигнала?

Варианты ответов: 1: Дискретен. 2: Непрерывен. 3: Может быть любым.

Ответ – 1.

ВОПРОС 2 Укажите формулу вычисления фазовой задержки фильтра.

Варианты ответов: 1: ω/. 2: dω/d(). 3: /ω. 4: d()/dω.

Ответ – 3.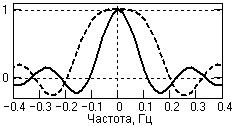



ВОПРОС 3. На рисунке приведены передаточные функции сглаживающих цифровых фильтров МНК первого и второго порядка с одинаковой шириной окна (операторы равного размера). Фильтр какого порядка будет вносить искажения в низкочастотные сигналы в минимальной степени?

Варианты ответов: 1- первого, 2- второго.

Ответ – 2.

ВОПРОС 4. Как при дифференцировании сигнала изменяется его спектр в области низких (НЧ) и высоких (ВЧ) частот?

Варианты ответов:

1: соотношение частот не изменяется, 2: увеличиваются ВЧ,

3: амплитуды ВЧ возрастают, а НЧ уменьшаются, 4: увеличиваются НЧ.

5: амплитуды НЧ возрастают, ВЧ уменьшаются,

Ответ – 3.

ВОПРОС 5. При усечении операторов идеальных частотных полосовых фильтров на скачках передаточных функций операторов возникает явление Гиббса. Может ли значение амплитуды выбросов явления Гиббса превышать 10% от величины скачка передаточной функции?

Варианты ответов: 1- да, 2- нет.

Ответ – 1.

ВОПРОС 6. При усечении операторов идеальных частотных фильтров на скачках передаточных функций операторов возникает явление Гиббса. Как можно нейтрализовать явление Гиббса?

Варианты ответов: 1- Увеличением окна оператора. 2- Уменьшением окна оператора. 3- Умножением оператора на весовую функцию. 4- Сглаживанием оператора весовой функцией.

Ответ – 4.

ВОПРОС 7. Какой подстановкой значения z выполняется преобразование z-образа фильтра в его частотную характеристику?

Варианты ответов: 1: exp(-jt). 2: exp(-t). 3: exp(-jt)).

Ответ – 1.

ВОПРОС 8. Укажите уравнение системы при реализации рекурсивного цифрового фильтра в каскадной форме.

Варианты ответов: 1: . 2: H_o(z) B_n(z) / [1+A_n(z)].

Ответ – 1.

ВОПРОС 9. Z-преобразование связано с деформацией частотной шкалы непрерывных функций в частотную шкалу главного частотного диапазона цифровых функций. В какой шкале задаются значения граничных частот фильтрации при проектировании рекурсивных фильтров?

Варианты ответов: 1- цифровых функций. 2- непрерывных функций.

Ответ – 2.

ВОПРОС 10. Система задана конечным оператором h(n). С использованием какой формулы вычисляется оператор деконволюции данной системы?

Варианты ответов: 1: 1/h(n). 2: 1). 3: _o/h(n).

4: H*()/А(). 5: 1/ h_k z^k. 6: H*()/[|H()|²+g²].

Ответ – 5.

ВОПРОС 11. Укажите уравнение, которым задается модель белого шума q(t) на входе фильтра?

Варианты ответов: 1: _i a_i(t-t_i). 2: a_i h(t-t_i). 3: c² R_h().

Ответ – 2.

ВОПРОС 12. Вашим заданием при проектировании нерекурсивного частотного цифрового фильтра ограничено количество членов фильтра окном (2N+1). Какую минимальную ширину переходной зоны можно достигнуть таким оператором без применения весовых функций?

Варианты ответов: 1- 2/(2N+1). 2- /(2N+1).

3- 2/(N+1). 4- /(N+1).

Ответ – 3.

В 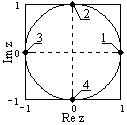ОПРОС 13. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота =/2?

Варианты ответов: 1, 2, 3, 4.

Ответ – 3.

ВОПРОС 14. Под каким углом в z-плоскости находится радиус-вектор нуля и полюса передаточной функции рекурсивного цифрового фильтра режекции постоянной составляющей данных?

Варианты ответов: 1- 0^о. 2- 90^о. 3- 180^о. 4- определяется расчетом.

Ответ – 4.

ВОПРОС 15. Z-преобразование связано с деформацией частотной шкалы непрерывных функций в частотную шкалу главного частотного диапазона цифровых функций. Какие значения граничных частот фильтрации задается при аппроксимации передаточной функции рекурсивных фильтров?

Варианты ответов: 1- требуемые частоты фильтрации.

2- деформированные частоты фильтрации.

Ответ – 1.

ВОПРОС 16. Система задана конечным оператором h(n). С использованием какой формулы вычисляется оптимальный оператор деконволюции данной системы?

Варианты ответов: 1: 1/h(n). 2: 1). 3: _o/h(n).

4: H*()/А(). 5: 1/ h_k z^k. 6: H*()/[|H()|²+g²].

Ответ – 6.

ВОПРОС 17. Какой критерий используется для проектирования фильтра при постановке задачи обнаружения (установления факта наличия) в экспериментальных данных сигнала известной формы?

Варианты ответов:

1: Максимум амплитудного отношения сигнал/шум на выходе фильтра.

2: Максимум энергетического отношения сигнал/шум.

3: Минимум среднего квадратического отклонения профильтрованного сигнала от его действительного или заданного значения.

Ответ – 3.

Дата: 04.04.2022
ТЕСТ № 2 Студент группы З-БА-ИТСС-18 Решетников Игорь Владимирович

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

ВОПРОС 1. Что представляет собой импульсный отклик дискретной линейной системы?

Варианты ответов: Это выходной сигнал системы при подаче на ее вход:

1: гармонического сигнала, 2: дельта-функции.

3: импульса Кронекера. 4: произвольного сигнала с единичной площадью.

Ответ – 2.

ВОПРОС 2. Что изменится в непрерывном (аналоговом) спектре массива произвольных данных, если осуществить продление массива нулевыми значениями?

Варианты ответов: 1: изменится модуль спектра. 2: изменится аргумент спектра.

3: изменятся модуль и аргумент. 4: ничего не изменится.

Ответ – 4.

ВОПРОС 3. Какими типами фильтров выполняется интегрирование данных?

Варианты ответов: 1- нерекурсивными, 2- рекурсивными.

Ответ – 1.

ВОПРОС 4. Как при интегрировании сигнала изменяется его спектр в области низких (НЧ) и высоких (ВЧ) частот?

Варианты ответов:

1: соотношение частот не изменяется, 2: увеличиваются ВЧ,

3: амплитуды ВЧ возрастают, а НЧ уменьшаются, 4: увеличиваются НЧ.

5: амплитуды НЧ возрастают, ВЧ уменьшаются,

Ответ – 2.

ВОПРОС 5. При усечении операторов идеальных частотных полосовых фильтров на скачках передаточных функций операторов возникает явление Гиббса. Зависит ли амплитуда пульсаций явления Гиббса от положения скачка в главном частотном диапазоне?

Варианты ответов: 1- да, 2- нет.

Ответ – 2.

ВОПРОС 6. Чему равна сумма коэффициентов операторов дифференцирующих фильтров?

Варианты ответов: 1- нулю. 2- единице. 3- зависит от порядка оператора.

4- может быть произвольной.

Ответ – 1.

В ОПРОС 7. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота =0?

Варианты ответов: 1, 2, 3, 4.

Ответ – 1.

ВОПРОС 8. Укажите уравнение системы при реализации рекурсивного цифрового фильтра в параллельной форме.

Варианты ответов: 1: . 2: H_o(z) B_n(z) / [1+A_n(z)].

Ответ – 2.

ВОПРОС 9. Z-преобразование связано с деформацией частотной шкалы непрерывных функций в частотную шкалу главного частотного диапазона цифровых функций. В какой шкале задается аппроксимация передаточной функции при проектировании рекурсивных фильтров?

Варианты ответов: 1- цифровых функций. 2- непрерывных функций.

Ответ – 2.

ВОПРОС 10. Система задана конечным оператором h(n). С использованием какой формулы вычисляется оптимальный оператор деконволюции данной системы?

Варианты ответов: 1: 1/h(n). 2: 1). 3: _o/h(n).

4: H*()/А(). 5: 1/ h_k z^k. 6: H*()/[|H()|²+g²].

Ответ – 5.

ВОПРОС 11. Укажите уравнение, которым задается модель белого шума g(t) на выходе фильтра h(t)?

Варианты ответов: 1: _i a_i(t-t_i). 2: a_i h(t-t_i). 3: c² R_h().

Ответ – 3.

ВОПРОС 12. Вашим заданием при проектировании нерекурсивного частотного цифрового фильтра ограничено количество членов фильтра окном (2N+1). Какую минимальную ширину переходной зоны можно достигнуть таким оператором c применением весовых функций?

Варианты ответов: 1  2/(2N+1). 2  /(2N+1).

3  2/(N+1). 4  /(N+1).

Ответ – 2.

В ОПРОС 13. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота =?

Варианты ответов: 1, 2, 3, 4.

Ответ – 3.

ВОПРОС 14. Сколько пар нулей и полюсов имеет передаточная функция рекурсивного цифрового фильтра режекции постоянной составляющей данных?

Варианты ответов: 1, 2, 3, 4- определяется расчетом.

Ответ – 1.

ВОПРОС 15. По какому аргументу задается аппроксимация передаточной функции при проектировании рекурсивных цифровых фильтров?

Варианты ответов: 1- по времени. 2- по частоте фильтрации.

3- по относительной частоте фильтрации.

Ответ – 1.

ВОПРОС 16. Система задана конечным оператором h(n). С использованием какой формулы вычисляется оператор неполной деконволюции данной системы (оператор сжатия сигналов)?

Варианты ответов: 1: 1/h(n). 2: 1). 3: _o/h(n).

4: H*()/А(). 5: 1/ h_k z^k. 6: H*()/[|H()|²+g²].

Ответ – 5.

ВОПРОС 17. Какой критерий используется для проектирования фильтра при постановке задачи обнаружения (установления факта присутствия) сигнала в экспериментальных данных?

Варианты ответов:

1: Максимум амплитудного отношения сигнал/шум на выходе фильтра.

2: Максимум энергетического отношения сигнал/шум.

3: Минимум среднего квадратического отклонения профильтрованного сигнала от его действительного или заданного значения.

Ответ – 3.

Дата: 05.04.2022