Урок геометрии в 10 классе. Угол между прямой и плоскостью_. Вводим понятие проекции точки на плоскость, проекции фигуры на плоскость. Определение
 Скачать 113 Kb.
|
 Вводим понятие проекции точки на плоскость, проекции фигуры на плоскость. Определение: Проекцией точки на плоскость называется основание перпендикуляра, проведённого из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости. Отметим вне α ещё три точки А, В, С, не лежащие на одной прямой. Соединим их попарно. 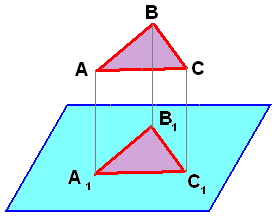 Вывод: Если построить проекции всех точек какой-нибудь фигуры на данную плоскость, то получим фигуру, которая называется проекцией. Докажем, что проекцией прямой а на плоскость α, не перпендикулярную к этой прямой, является прямая. Дано: а  α =О, а α.Д  оказать: проекцией а на α является а1Доказательство: 1) М  а, МН α. Проведём  через а и МН,  а1.2) Возьмём М1  , М1Н1 МН, М1Н1 а1=Н1. 3) Так как М1Н1 МН, и МН а1  М1Н1 α, то есть Н1 проекция М1 на плоскость .Что мы доказали? Ч 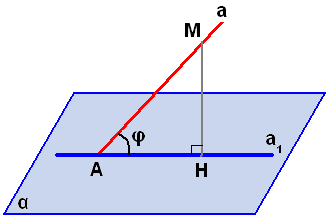 то проекция любой точки прямой а лежит на прямой а1. а1проекция прямой а на плоскость .Определение: Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней, называется угол между прямой и её проекцией на плоскость.   (а, )=900 (а, )=00 Задача 1: В параллелепипеде ABCDA1B1C1D1 - ABCD – квадрат со стороной, равной 2 см. Все боковые грани – прямоугольники, B1D=5 см. Найдите углы между B1D и плоскостью ABC и между B1D и плоскостью DD1C1. Р  ешение: 1. ABCD – квадрат. По теореме Пифагора BD2=22+22=8; BD=2  ; 2. cos BDB1=0,4 ; BDB1=550333. sin B1DC1=0,4; 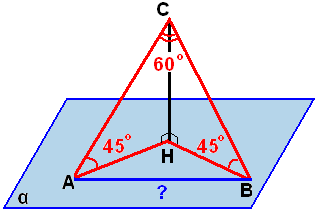B1DC1=23035 Задача 2: Из точки, отстоящей от плоскости на расстояние а, проведены две наклонные, образующие с плоскостью углы в 450, а между собой угол в 600. Определить расстояние между концами наклонных. Решение: 1. Треугольники ACH и СHB прямоугольные и САН= СВН=45о СН=АН=НВ=а2. По теореме Пифагора СА=СВ=а ;3. В треугольнике АВС АСВ=60о и АС=СВ треугольник АВС равносторонний - 5 - АВ= а ;ДОМАШНЕЕ ЗАДАНИЕ п.21 №164, 165 |