задачи по статистике. Задачи 1 2 3 варианта 5. Задача 1 Имеются следующие данные по 20 магазинам за квартал
 Скачать 41.22 Kb.
|
|
Задача 1 Имеются следующие данные по 20 магазинам за квартал: Таблица 1.1 Исходные данные
Проведите аналитическую группировку. По каждой группе подсчитайте: 1) число магазинов; 2) товарооборот на один магазин; 3) товарные запасы в среднем на один магазин. Сделайте выводы. Решение Для группировки магазинов по величине товарооборота с равным интервалом, используя формулу: 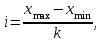 где xmax, xmin – максимальное и минимальное значения признака. Для 20 наблюдений сгруппируем данные по 4 группам. Равный интервал: 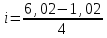 = 1,25 млн. руб.Результаты группировки. представлены в таблице 1.2. Таблица 1.2 Группировка магазинов по величине товарооборота
Данная группировка является аналитической, поскольку в ее основе – факторный признак (величина товарооборота) и каждая группа характеризуется средними значениями результативного признака (среднегодовой величиной запасов). Группировка является простой, поскольку группы образованы только по одному признаку. По результатам группировки можно заключить, что наименьшее число магазинов (по 4 шт) было в группах меньшим товарооборотом (1,02-2,27 и 2,27-3,52 млн. руб.), а наибольшее число магазинов (по 6 шт) – в группах с большим объемом товарооборота (3,52-4,77 и 4,77-6,02 млн. руб.). Можно отметить, что большей средней величине товарных запасов соответствует больший объем товарооборота. Задача 2 Имеются данные о ценах и продаже моркови на колхозном рынке: Таблица 2 Исходные данные
Вычислить среднюю цену на морковь за три месяца, применяя в качестве весов: а) реализацию в натуральных показателях; б) товарооборот в рублях. Решение а) При расчете средней цены на морковь, применяя в качестве весов объем реализации в натуральных показателях, используем формулу средней арифметической взвешенной: 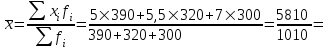 5,75 руб.б) При расчете средней цены на морковь, применяя в качестве весов стоимостной объем товарооборота, используем формулу средней арифметической взвешенной: 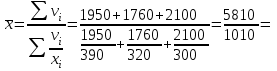 5,75 руб.Задача 3 В целях изучения производительности труда токарей на предприятии было проведено 10 %-е выборочное обследование 100 рабочих методом случайного отбора. В результате обследования получены данные о затратах времени на обработку одной детали: Таблица 3 Исходные данные
В каких пределах находится доля рабочих, затрачивающих на обработку одной детали 25 минут и более? Решение Границы генеральной доли (р) определяются по формуле: 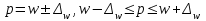 где 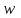 – выборочная доля (отношение единиц, обладающих изучаемым признаком к объему выборки);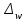 – предельная ошибка выборочной доли.Количество рабочих затрачивающих на обработку одной детали 25 минут и более – 66 человек (50+12+4), т.е. выборочная доля составит: 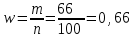 Средняя погрешность доли при бесповторном отборе: 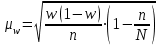 где n – объем выборки; N – объем генеральной совокупности. Предельная ошибка выборки при бесповторном отборе определяется по формуле: 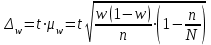 где t – коэффициент доверия, который зависит от значения вероятности Р(t); 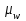 – средняя погрешность доли; n – объем выборки; N – объем генеральной совокупности. Объем выборки n=100 человек, т.е. при 10% выборке объем генеральной совокупности N=1000 чел. Средняя погрешность доли составила: 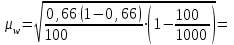 0,045В данном случае не задана вероятность, от которой зависит значение коэффициента доверия t и, соответственно, предельная ошибка. Например, при вероятности Р(t) = 0,954 по таблице значений функций φ(t), которая выражается интегральной формулой Лапласа, t = 2, тогда Предельная ошибка составит: 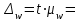 2∙0,045=0,09Пределы доли рабочих, затрачивающих на обработку одной детали 25 минут и более: 0,66–0,09 ≤ р ≤ 0,66+0,09 0,57 ≤ р ≤ 0,74 Таким образом, с вероятностью 0,954 можно утверждать, что пределы доли рабочих, затрачивающих на обработку одной детали 25 минут и более в выборке составят от 57% до 74% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||