|
|
презентация методы педагогики. Методы обучения и воспитания Задание к зачету 21. Трипузова Кари. Задача 1 На уроках математики ученики произносили следующие фразы (см в таблице)
ЗАДАНИЕ К ЗАЧЕТУ
2021
ЗАДАЧА № 1
На уроках математики ученики произносили следующие фразы (см. в таблице).
Задание. Укажите правомерность произношения каждой фразы. Неправильные фразы переформулируйте так, чтобы они звучали математически корректно и стилистически грамотно.
№
|
Фразы учеников
|
Оценка
(+/–)
|
Правильные фразы
|
1
|
«сократим уравнение на одно и то же число»
|
-
|
Разделим обе части уравнения на одно и то же число. ИЛИ Сократим дробь.
|
2
|
«решим треугольник по двум сторонам и углу между ними»
|
-
|
Построим треугольник по двум сторонам и углу между ними.
|
3
|
«скобка равна нулю»
|
-
|
Выражение в скобке равно нулю.
|
4
|
«решим задание»
|
-
|
Выполним задание. ИЛИ Решим задачу.
|
5
|
«читаем график»
|
-
|
Изучим график. ИЛИ Исследуем график.
|
6
|
«проведем окружность из точки А»
|
-
|
Построим окружность с центром в точке А.
|
7
|
«запишем в процентах десятичную дробь»
|
+
|
|
8
|
«−6 всегда меньше, чем 5»
|
-
|
-6 всегда меньше 5
|
9
|
«разобьем площадь многоугольника на треугольники»
|
+
|
|
10
|
«освободимся от иррациональности в знаменателе»
|
-
|
Избавимся от иррациональности в знаменателе.
|
ЗАДАЧА № 2
Правильно ли даны определения понятий? Если нет, назовите, какое требование к определениям нарушено (вид ошибки: широкое, узкое; логически не минимальное). Дайте правильное определение понятия.
Математическое
предложение
|
Оценка:
(правильно,
недочет, ошибка)
|
Вид
ошибки
|
Правильное
определение
|
1. Средней линией трапеции называют отрезок, соединяющий середины противоположных сторон трапеции.
|
Ошибка
|
Широкое
|
Средней линией трапеции называется отрезок, соединяющая середины боковых сторон и расположен параллельно основаниям.
|
2. Пирамиду называют правильной, если стороны основания равны и вершина пирамиды проектируется в центр основания.
|
Правильно
|
|
|
3. Прямоугольником называют четырехугольник, у которого диагонали равны.
|
Ошибка
|
Широкое
|
Прямоугольник — четырёхугольник, у которого все углы прямые
|
4. Квадратным уравнением называют уравнение вида ах2 + bх +с = 0, где х – переменная, а,b, с – некоторые числа.
|
Ошибка
|
Не полное определение
|
Квадратным уравнением называют уравнение вида a x 2 + bx + c = 0 , где коэффициенты a, b, c — любые действительные числа, причём a ≠ 0
|
5. Правильной дробью называют дробь, значение которой больше 0, но меньше 1.
|
Ошибка
|
|
дробь называется правильной, если ее числитель меньше знаменателя
|
6. Ромбом называют параллелограмм, у которого есть две равные смежные стороны.
|
Ошибка
|
|
Ромб это Параллелограмм, все стороны к-рого равны, а углы непрямые
|
7. Диаметром окружности называют наибольшую хорду
|
Правильно
|
|
|
8. Диаметром окружности называют два радиуса.
|
Ошибка
|
|
Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.
|
9. Две прямые в пространства называют перпендикулярными, если они пересекаются под прямым углом.
|
Правильно
|
|
|
ЗАДАЧА № 3
В учебнике «Геометрия 10-11» Л.С. Атанасяна дается следующее определение прямой, перпендикулярной плоскости: «Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости». Однако на уроке ученики привели другие формулировки этого понятия (см. в таблице). Прокомментируйте ответы ученика.
Формулировки, которые привели ученики
|
Комментарий учителя
|
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.
|
Верно.
|
Прямая называется перпендикулярной к плоскости, если она пересекает плоскость под углом 90◦.
|
Верно.
|
ЗАДАЧА № 4
Задание. Напишите 5 утверждений, являющихся отличительными характеристиками прямого угла.
1
|
Прямой угол равен 90 градусов.
|
2
|
Величина прямого угла 324000 угловых секунд.
|
3
|
Прямой угол единственный, который отмечается углом. Остальные углы отмечаются дугами.
|
4
|
Прямой угол составляет половину развернутого угла.
|
5
|
Прямой угол образуется при пересечении двух перпендикулярных прямых.
|
ЗАДАЧА № 5
Решая задачу «Две бригады, работая совместно, закончили работу за 4 дня. Сколько дней потребовалось бы каждой бригаде отдельно, если первая бригада могла бы закончить работу на 6 дней раньше второй?», ученики получили следующие уравнения (см. в таблице).
Задание. Оцените (правильно / неправильно) правильность составления каждого уравнения. В том случае, если уравнение составлено правильно, укажите, какая величина обозначена за х, а также запишите, что обозначает каждое выражение, входящее в уравнение. Результаты оформите таблицей.
Уравнение
|
Оценка
|
Название величины, обозначенной за х
|
Название величин, входящих в уравнение
|

|
Неверно
|
х – это …
|
|

|
Верно
|
х – это … Количество дней, которое потребуется 1 бригаде
|
|

|
Неверно
|
х – это …
|
|

|
Неверно
|
х – это …
|
|
ЗАДАЧА № 6
Ученику 8 класса была задана на дом следующая задача:
По тропинке вдоль кустов шло 11 хвостов.
Насчитать я также смог, что шагало 30 ног.
Это дружно шли куда-то петухи и поросята.
А теперь вопрос таков: «Сколько было петухов?»
Спрошу также у ребят: «Сколько было поросят?»
Однако эту задачу удалось решить и его младшему брату, ученику 5 класса.
Задание: Представьте возможные варианты решения задачи учащимися:
1) 5-6 классов (использовать арифметический метод решения).
2) 7-9 классов (использовать алгебраический метод решения).
Решение задачи арифметическим методом
|
Решение задачи алгебраическим методом
|
Если считать у каждого по 2 ноги то ног 11*2= 22 ноги. Но всего ног было 30 Найдём разницу 30-22= 8 ног приходится на поросят. Значит поросят 8:2=4
Т.Е. поросят 4 штуки. А петухов 11-4= 7 штук.
Ответ: 4 Поросят и 7 Петухов.
|
В условии задачи содержится подсказка – 11 хвостов, ровно столько животных шло по тропинке. Пусть поросят было х (икс), тогда петухов – (11- х). Тогда у поросят: 4 • х ног, а у петухов: 2 • (11 – х) ног. Зная общее количество ног у этих животных, составим уравнение:
4 • х + 2 • (11 – х) = 30;
4 • х + 22 – 2 • х = 30;
2 • х = 30 – 22;
2 • х = 8;
х = 8 : 2;
х = 4 – было поросят;
11- х = 11 – 4 = 7 – было петухов.
Ответ: по тропинке шли 4 поросенка и 7 петухов.
|
ЗАДАЧА № 7
1. Проверьте, правильно ли ученик выполнил задание «Найдите экстремумы функции  » (см. ниже).. » (см. ниже)..
1. Если нет, то приведите правильное решение.
2. Изобразите схематично график функции.
Решение ученика
|
Правильное решение
|


 
4)
Ответ: уmax = 1 при хmax = 1.
|

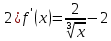
3) 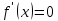
  X= 1 X= 1
 Теперь найдем критические точки, в которых производная функции не определена, однако функция определена Теперь найдем критические точки, в которых производная функции не определена, однако функция определена
Х=1
Х=0

   х х
+ 0 - 1 +
Локальный максимум 1 в точке х=1
Локальный минимум 0 в точке х=0
|
2. Изобразите схематично график функции.
  у у


0 х
ЗАДАЧА № 8

Решение

𝐵𝐻 + 𝐻𝐶 = 6
Треугольник со сторонами 4,8 и 6 существует. Значит Николай был прав, а Петр ошибся.
Ответ: Николай был прав. |
|
|
 Скачать 0.97 Mb.
Скачать 0.97 Mb. » (см. ниже)..
» (см. ниже).. 
 у
у












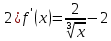
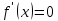

 X= 1
X= 1 Теперь найдем критические точки, в которых производная функции не определена,
Теперь найдем критические точки, в которых производная функции не определена, 


 х
х