Документ Microsoft Word. Задача 1С Плоская система сходящихся сил Плоская система сходящихся сил находится в равновесии. Определите усилия, возникающие в системе согласно вариантам, приведенным в таблице 1

• Название: Задача 1С Плоская система сходящихся сил Плоская система сходящихся сил находится в равновесии. Определите усилия, возникающие в системе согласно вариантам, приведенным в таблице 1
• Дата: 17.01.2019
• Размер: 1.68 Mb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Задача; #64052

Задача 1-С: Плоская система сходящихся сил Плоская система сходящихся сил находится в равновесии. Определите усилия, возникающие в системе согласно вариантам, приведенным в таблице 1.

Решение.





Составляем уравнения равновесия:




Выражаем Т из первого уравнения:


Подставляем Т во второе уравнение:





Ответ: 6
Задача 2-С: Плоская система произвольно расположенных сил На жесткую раму действует пара сил с моментом M  60 Н  м и две силы (номера, величины, направление и точки приложения сил приведены в таблице 1, схемы рам показаны на рис. 1–6), a  0.5 м. Определить реакции связей (опорные реакции) в точках А и В с помощью аналитических условий равновесия. Убедиться в правильности решения, выполнив проверку.





Решение. Рассмотрим равновесие системы:

1. Вводим оси координат Ox Oy .

2. Отбрасываем связи. Действие связей заменяем силами реакции связей. В точке А шарнирно-неподвижная опора. Неизвестную силу реакции связи раскладываем на составляющие , . В точке В шарнирно-подвижная опора. Неизвестную силу реакции связи направляем по нормали к опорной поверхности.
3. Записываем условия равновесия плоской системы сил:













4. Решаем систему 3-х алгебраических уравнений.
Из уравнения (1):



Из уравнения (3):



Из уравнения (2):


5. Для проверки правильности решения задачи убедимся в том, что соблюдается уравнение равновесия для сил.



60+(
Ответ: ; ; .
Задача 3-С: Плоская система произвольно расположенных сил. На жесткую раму действуют силы, указанные в таблице 1. Схемы конструкции рам представлены на рис. 1–3. Определить реакции связей (опорные реакции) в конструкции с помощью аналитических условий равновесия. Убедиться в правильности решения, выполнив проверку.






Решение. Рассмотрим систему уравновешивающих сил.










Из уравнения (1):

-3,242

Из уравнения (2):



Из уравнения (3):


Для проверки решения задачи убедимся в том, что соблюдается уравнение равновесия для сил.



Ответ: ;
Задача 4-С: Плоская система произвольно расположенных сил

На жесткую раму действуют силы, указанные в таблице 1. Схемы конструкции рам представлены на рис. 1–3. Определить реакции связей (опорные реакции) и давление в промежуточном шарнире составной конструкции (система двух тел) с помощью аналитических условий равновесия. Убедиться в правильности решения, выполнив проверку.

14

7

6

15

1,1

Решение. Сначала рассмотрим систему уравновешивающихся сил, приложенных к левой части конструкции.

Равномерно-распределенную нагрузку q заменяем сосредоточенной силой Q: Q=2q=2*1,1=2,2 кН*м
Уравнения равновесия имеют вид:







Из уравнения (3):



Из уравнения (1):



Из уравнения (2):


Рассмотрим теперь систему уравновешивающихся сил, приложенных к правой части конструкции:

Уравнения равновесия для всей системы:






Из 1 уравнения:



Из 2 уравнения:



Из 3 уравнения:


Для проверки правильности решения задачи убедимся в том, что соблюдается уравнение равновесия для сил, приложенных ко всей конструкции:
  

 0


Ответ:




Задача 5-С: Пространственная система произвольно расположенных сил Плита весом P =3 кН со сторонами AB  3a , BC  2a закреплена в точке А сферическим, а в точке В цилиндрическим шарниром и удерживается в равновесии невесомым стержнем CC (Рис. 1 – 6). На плиту действует пара сил с моментом M =5 кН  м , лежащая в плоскости плиты, и две силы (номера, величины, направление и точки приложения сил приведены в таблице 1). Точки приложения сил D, E, H находятся на серединах сторон плиты, a  0.8 м. Определить реакции связей (опорные реакции) в точках А, В и С.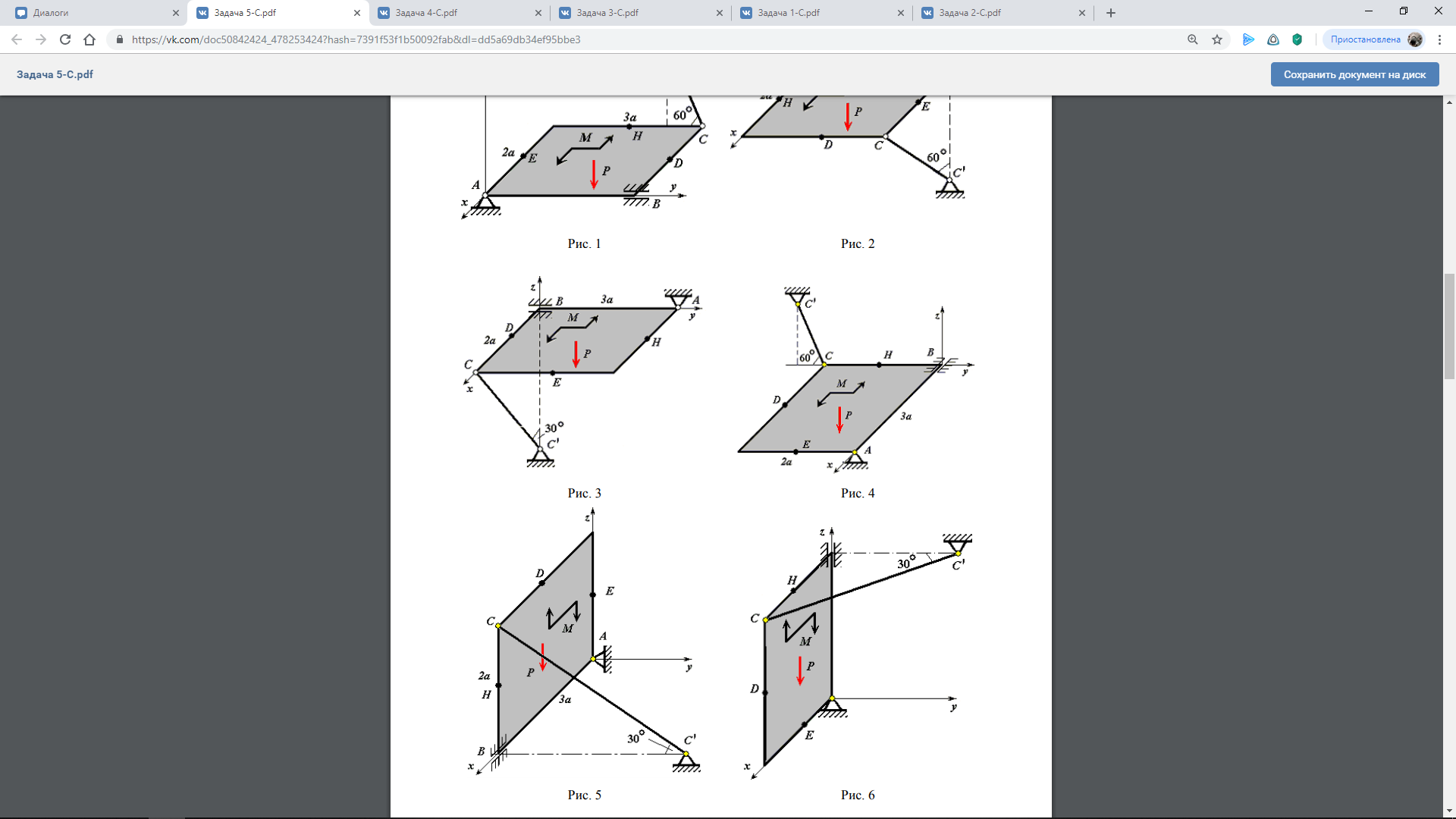







Решение. Рассмотрим равновесие рамы. На нее действуют заданные силы P , F₂ , F₄ и пара сил с моментом M.

Отбрасываем связи. Действие связей заменяем силами реакции связей. В точке А сферический шарнир. Неизвестную силу реакции связи R_А раскладываем на составляющие, параллельные осям координат. В точке В цилиндрический шарнир. Неизвестную силу реакции связи раскладываем на составляющие, параллельные осям координат и лежащие в плоскости, перпендикулярной оси шарнира.

Записываем условия равновесия системы сил:

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   

Из 1 уравнения:



Из 4 уравнения:



Из 5 уравнения:



Из 6 уравнения:



Из 2 уравнения:



Из 3 уравнения:



Ответ:







Решение. Строим положение механизма в соответствии с заданными углами.


Определяем направления скоростей точек A, B, E. Строим перпендикуляры к скоростям и и на их пересечении получаем мгновенный центр скоростей для стержня 3.

Треугольник прямоугольный, угол равен 30 , следовательно:

sin30,

cos30 м.

:







Строим перпендикуляры к скоростям и и на их пересечении получаем мгновенный центр скоростей Р2 для стержня 2 .

Треугольник прямоугольный, угол равен 60 , следовательно, угол равен 30, следовательно:

,

sin60 м.

равно:



:



Ответ: ; ;