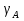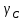Контрольная работа Вариант 4 (только 3 задачи). Задача Двухступенчатый стальной брус, длины ступеней которого в миллиметрах указаны на схеме, нагружен силами F
 Скачать 36.37 Kb. Скачать 36.37 Kb.
|
|
Задача 1. Двухступенчатый стальной брус, длины ступеней которого в миллиметрах указаны на схеме, нагружен силами F1 и F2. Построить эпюры продольных сил и нормальный напряжений по длине бруса. Определить перемещение ∆l нижнего торцевого сечения бруса, приняв E = 2*105 МПа. Числовые значения F1 и F2 , а также площади поперечных сечений A1 и A2 указаны в таблице. Таблица 1
Решение Разделим брус на участки, границы которых определяются сечениями, где изменяться площадь поперечного сечения или приложены внешние нагрузки. Рассмотрим первый участок , отбросив верхнюю часть. Силы F1 и F2 уравновешиваются внутренней продольной силой и равна алгеброической сумме : NZ1 = - F1 + F2 = -1,6 + 3,8 = 2,2 кН Аналогично, при рассмотрении последующих участков : NZ2= NZ3= NZ1 = - F1 + F2= 2,2 кН Построим эпюру NZ. Т.к. у нас все продольные силы имеют положительный знак , следовательно по всей длине брус будет растянут. Для определения напряжений в поперечных сечениях значение продольных сил необходимо разделить на площади соответствующих сечений. Площадь поперечного сечения бруса : в пределах участка I и II AI= AII= A1= 0,2 см2= 2 * 10-5 м2 в пределах участка III AIII= A2= 0,6 см2= 6 * 10-5 м2 Находим напряжение на отдельных участках бруса и строим эпюру σI = NZ1 / AI= 2,2 *103 /2 * 10-5 = 110 * 106 Н/м2 = 110 МПа; σII = NZ2 / AII= 2,2 *103 /2 * 10-5 = 110 * 106 Н/м2 = 110 МПа; σIII = NZ3 / AIII= 2,2 *103 /6 * 10-5 = 36,6 * 106 Н/м2 = 36,67 МПа; В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений. Полное удлинение бруса равно алгебраической сумме удлинений его участков ∆l=1/E *(σI*lI + σII*lII+ σIII*lIII ) = 1/2* 1011 * (110*106*0,16 + 110*106*0,04 + 36,67*106*0,2)= =29,34*106 / 2*1011 =14,67 *10 -5м = 0,1467 мм Ответ: ∆l = 0,1467 мм. Задача 2. Биметаллический провод подвешивается на горизонтальном пролете l. Требуется определить: а) стрелу провисания ʄ1 в летних условиях с тем, чтобы в зимних условиях напряжение в проводе не привысило допускаемое; б) распределение усилий и напряжений по различным материалам биметеллического провода в летних и зимних условиях; в) «тяжение» провода в летних и зимних условиях N1 и N2. Дать заключение о запасе прочности в различных частях провода. Данные своего варианта взять из таблицы
Используемые формулы: 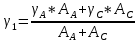 [2.1] [2.1]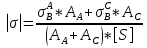 [2.2] [2.2]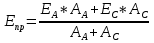 [2.3] [2.3]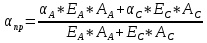 [2.4] [2.4]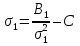 [2.6] [2.6]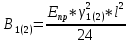 [2.7] [2.7]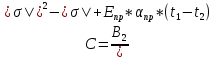 [2.8] [2.8]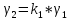 [2.9] [2.9]Решение: Составим таблицу механических характеристик составных частей провода
Определим «приведенные» величины биметаллического провода по формулам (2.1)-(2.4). Причем для ускорения вычисления эти формулы следует упростить, разделив числители и знаменатели формул (2.1)-(2.3)на АС, а формулу (2.4) – на произведение ЕС*АС . 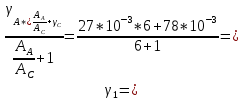 34,28*10-3 Н/м *мм2 34,28*10-3 Н/м *мм2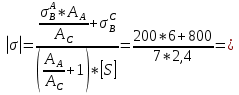 119,05 Н/мм2 119,05 Н/мм2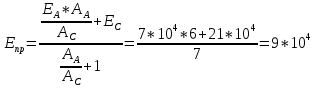 Н/мм2 Н/мм2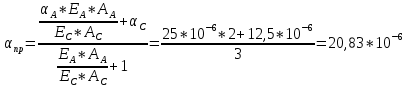 1/град 1/градПо формулам (2.7)-(2.9) вычислим вспомогательные элементы. 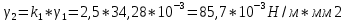 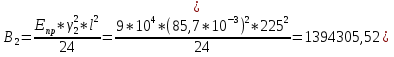 Н/мм2)3 Н/мм2)3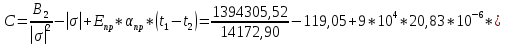 * 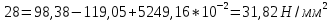 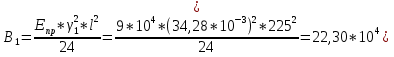 Н/мм2)3 Н/мм2)3Найденные значения позволяют составить «уравнение состояния провода»(2.6): 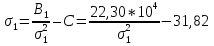 Решаем уравнение методом подбора. Возьмем 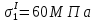 . При подстановке оказывается это число не подходит. Вторая проба числа . При подстановке оказывается это число не подходит. Вторая проба числа 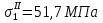 дает хорошее приближение. Окончательно дает хорошее приближение. Окончательно 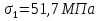 . .Обобщаем и анализируем полученные результаты. Необходимая стела провисания: летом 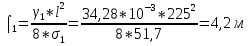 зимой 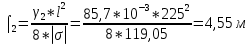 Близость результатов указывает на то, что зимняя нагрузка 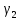 скомпенсировала температурное укорочение провода. скомпенсировала температурное укорочение провода.Летнее и зимнее «тяжение» провода: 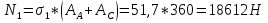 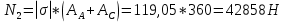 Из соотношений 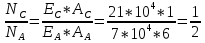 найдем найдем 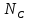 и и 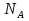 в летние и зимние периоды: в летние и зимние периоды: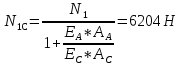 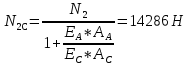 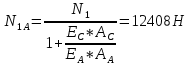 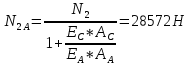 Определим напряжение в частях биметаллического провода. AA = A /7 *6 = 308,57 мм AС = A / 7 = 51,43 мм 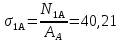 МПа МПа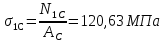 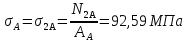 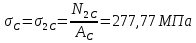 Оценка прочности частей биметаллического провода: 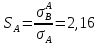 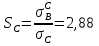 Вывод: так как 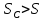 , а , а 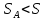 , то это значит, что прочностных характеристик стали достаточно, а алюминия — недостаточно. , то это значит, что прочностных характеристик стали достаточно, а алюминия — недостаточно.Задача 3. Определить положение центра тяжести тонкой однородной пластины, форма и размеры которой в миллиметрах указаны на рисунке. Данные для своего варианта взять из таблицы.
Решение Фигура состоит из 3 фигур 1 треугольника и 2 прямоугольников. Площадь отверстий прямоугольника 1 и треугольника 2 вводим со знаком «-» , а прямоугольника 3 вычисляем без учета имеющихся в нем отверстий.
Вычислим центр тяжести плоской фигуры по формулам: 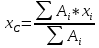 [3.1] [3.1]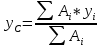 [3.2] [3.2]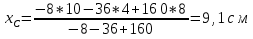 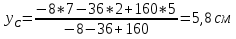 Ответ центр тяжести плоской фигуры имеет координаты xс = 9,1 см и yс = 5,8 см. Задача 4 Для двухопорной балки, нагруженной, как показано на рисунке, силами F1 и F2 и парой сил с моментом М, определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и подобрать необходимый размер поперечного сечения (двутавр или два швеллера), приняв [σ]= 160 МПа. Числовые значения величин для своего варианта задачи взять из таблицы.
Решение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

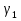 /
/