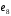дискретная. дискретка. Задача Построить таблицу истинности для заданной формулы. Обозначим F

• Название: Задача Построить таблицу истинности для заданной формулы. Обозначим F
• Анкор: дискретная
• Дата: 02.04.2022
• Размер: 84.32 Kb.
• Имя файла: дискретка.docx
• Тип: Задача; #436120

КОНТРОЛЬНАЯ РАБОТА


Условия задач

Задача 1. Построить таблицу истинности для заданной формулы.

1. 
   
   

2. 
   Обозначим F=
   

x1	x2	x3						F
0	0	0	1	1	0	1	1	1
0	0	1	1	1	0	0	0	1
0	1	0	1	1	1	1	1	1
0	1	1	1	1	1	0	0	0
1	0	0	0	0	1	1	0	0
1	0	1	0	0	1	0	0	0
1	1	0	0	1	1	1	1	1
1	1	1	0	1	1	0	0	0

Задача 2. Преобразовать данную формулу так, чтобы она содержала только операции тесного отрицания, дизъюнкции и конъюнкции. Пользуясь свойствами операций дизъюнкции и конъюнкции, привести формулу к виду, не содержащему скобок.
2.

Будем использовать известные тождества

Законы де Моргана


.





Задача 3. Из колоды в 36 карт вынимают карт. Указать число наборов, содержащих ровно карт бубновой масти и карт пиковой масти. Рассмотреть случаи выбора с возвращением и без возвращения.
.

Случай 1. Выбор с возвращением.

Так как карта после выбора возвращается в колоду, количество бубновых (9 карт), пиковых (9 карт) и других карт (18 карт) в колоде не меняются. Тогда количество способов выбрать 8 карт из 36 так, чтобы из них 3 были бубновой масти будет 9*9*9, 2 карты пиковой масти будет 9*9 и еще оставшиеся 3 другой масти будет 18*18*18. При этом, так как выбор упорядоченный, карты можно переставлять между собой, число различных перестановок равно


Итого получаем 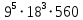способов.
Случай 2. Выбор без возвращения.
Нужно выбрать 8 карт из 36 так, чтобы из них 3 были бубновой масти (всего таких карт 9), 2 карты пиковой масти (всего таких карт 9) и еще 3 другой масти (всего их 18), откуда получаем по правилу умножения



способов (снова умножили на число способов упорядочить выбранные карты).

Задача 4. Пользуясь Алгоритмом Дейкстры, найти кратчайшие расстояния из вершины неориентированного взвешенного графа в другие вершины графа. Указать кратчайший маршрут из вершины в вершину .

	1	2	1	3	2	1	1	8	2	3

Решение.
Найдем кратчайший путь от вершины до всех вершин, используя алгоритм Дейкстры
Шаг 1. Начальная вершина v1 . Присвоим ей метку 0, остальным -

Шаг 2. Из вершины v1 можно попасть в v2,v3,v4,v6

L(v1,v2)=min{ ;0+1}=1

L(v1,v3)=min{ ;0+3}=3

L(v1,v4)=min{ ;0+8}=8

L(v1,v6)=min{ ;0+1}=1
min{1,3,8,1}=1 (вершина v2)
Шаг 3.
Из вершины v2 можно попасть в v3

L(v2,v3)=min{3;1+2}=3
min{3,8,1}=1 (вершина v6)
шаг 4.

Из вершины v6 можно попасть в v3,v4,v5

L(v6,v3)=min{3;1+1}=2

L(v6,v4)=min{8;1+2}=3

L(v6,v5)=min{ ;1+2}=3
min{2,3,3}=2 (вершина v3)
шаг 5.

Из вершины v3 можно попасть в v4 (остальные рассмотрены)

L(v3,v4)=min{4;3+1}=4

min{4,6}=4 (вершина v4)
шаг 6.

Из вершины v4 можно попасть в v5 (остальные рассмотрены)

L(v4,v5)=min{6;4+3}=6

шаг	v1	v2	v3	v4	v5	v6	расстояние	вершина
1	0						0	v1
2		1	4	7		2	1	v2
3			3	7		2	2	v6
4			3	4	6		3	v3
5				4	6		4	v4
6					6		6	v5

Задача 5. Схема дорог, соединяющих населенные пункты, задана графом, показанным на рисунке. В таблице каждому ребру графа поставлен в соответствие вес, характеризующий стоимость прокладки дороги, соединяющей данные населенные пункты. При помощи алгоритма Краскала построить схему дорог, соединяющих данные населенные пункты, при наименьшей стоимости проекта.

	1	2	1	2	1	3	1	2	1	1	3	1	1	2	1	3

Решение.
Найдем остовное дерево минимального веса (то есть схему дорог наименьшей стоимости) с помощью алгоритма Краскала. Пронумеруем вершины графа для удобства, ребра пометим весом (стоимостью) согласно варианту.
Начинаем с ребра минимального веса (x1,x2) , его вес равен 1.
Затем по очереди добавляем ребра минимального веса, так, чтобы они не образовали цикла. Порядок добавления:

Ребро (x1,x2), его вес равен 1.

ребро (x1,x4), его вес равен 1

ребро (x4,x5), его вес равен 1 .

ребро (x4,x3), его вес равен 1

ребро (41,x7), его вес равен 1

ребро (51,x6), его вес равен 1

ребро (x6,x9), его вес равен 1

ребро (x7,x8), его вес равен 1
Все вершины добавлены в дерево. Минимальное остовное дерево построено. Обведем его на чертеже:


Его вес равен 1+1+1+1+1+1+1+1=8

Задача 6. Выяснить, применима ли машина Тьюринга, заданная программой к слову 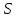и если применима, то указать результат применения машины Тьюринга к данному слову.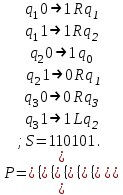

Решение.

Начальное состояние машины . Начнем применять машину, заданную программой P , к слову S . Двигаемся слева направо.

Шаг 1. Начальное слово ...0 110101... , состояние .

Многоточием обозначаем бесконечную ленту.
Шаг 2. Применяем правило 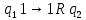то есть сдвигаемся вправо на 1, единица сохраняется, переходим в состояние .

Получаем слово:
Состояние .
Шаг 3. Применяем правило то есть сдвигаемся вправо на 1, единица сохраняется, переходим в состояние .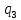

Получаем слово:

Состояние

Шаг 4. Применяем правило , то есть сдвигаемся вправо на 1, нуль меняется на 1, переходим в состояние .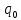

Получаем слово:
Состояние .
Так как мы пришли к конечному состоянию, программа машины Тьюринга применима к данному слову и переводит его в слово T =111101 (меняет первый нуль на 1).