Задачи на движение.. Задача Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 кмч
 Скачать 186.86 Kb. Скачать 186.86 Kb.
|
|
Задачи для самостоятельного решения Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч? Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь? Задача 3.Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист? Задача 4*.Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки? Задача 5.Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа? Задача 6.От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч? Задача 7.Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи? Задача 8.Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км? Задача 9.От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч? Задача 10*.Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км? Задача 11*.Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов? Задача 12.Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км? Задачи для самостоятельного решения Задача 1.Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч? Решение За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения 20 : 5 = 4 часа  Задача 2.Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь? Решение Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта Ав пункт В (16км/ч) на время движения (5ч) 16 × 5 = 80 км  Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч) 80 : 10 = 8 ч  Задача 3.Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист? Решение Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км) 83 − 11 = 72 км  Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов 72 : 6 = 12 км/ч Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче. Ответ:велосипедист ехал со скоростью 12 км/ч. Задача 4.Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки? Решение Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов 72 : 36 = 2 км/ч Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа 72 : 4 = 18 км/ч Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров 110 : 22 = 5 ч Ответ:по течению реки теплоход проплывет 110 километров на 5 часов. Задача 5.Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа? Решение Найдем скорость удаления велосипедистов 11 + 13 = 24 км Узнаем какое расстояние будет между ними через 4 часа 24 × 4 = 96 км/ч  Ответ:через 4 часа расстояние между велосипедистами будет 96 км. Задача 6.От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч? Решение Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч) 21 × 6 = 126 км Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч) 24 × 6 = 144 км Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами 126 км + 144 км = 270 км Ответ:первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км. Задача 7.Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи? Решение Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов 51 × 16 = 816 км Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы 1520 − 816 = 704 км Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов 704 : 16 = 44 км/ч Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5 51 км/ч + 44 км/ч = 95 км/ч 95 × 5 = 475 км. Ответ:поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км. Задача 8.Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км? Решение Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса 48 км/ч + 6 км/ч = 54 км/ч Найдем скорость удаления автобусов. Для этого сложим их скорости: 48 км/ч + 54 км/ч = 102 км/ч За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч 510 : 102 = 5 ч Ответ:510 км между автобусами будет через 5 часов. Задача 9.Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет  скорости московского поезда. На каком расстоянии от Ростова встретятся поезда? скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?Решение Найдем скорость ростовского поезда. Она составляет  скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти  от 63 км от 63 км63 : 21 × 20 = 3 × 20 = 60 км/ч Найдем скорость сближения поездов 63 км/ч + 60 км/ч = 123 км/ч Определим через сколько часов поезда встретятся 1230 : 123 = 10 ч Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи 60 × 10 = 600 км. Ответ:поезда встретятся на расстоянии 600 км от Ростова. Задача 10.От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч? Решение Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км 16 × 0,75 = 12 км/ч Найдем скорость сближения лодок 16 км/ч + 12 км/ч = 28 км/ч С каждым часом расстояние между лодками будет уменьшаться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км 75 км − 56 км = 19 км Ответ:через 2 часа между лодками будет 19 км. Скрыть решение Задача 11.Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км? Решение  Найдем скорость сближения 62 км/ч − 47 км/ч = 15 км/ч Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшаться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км 60 : 15 = 4 ч Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч) 62 × 4 = 248 км Ответ:легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения. Задача 12.Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов? Решение Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч 35 × 0,80 = 28 км/ч Первый мотоциклист двигается на 35-28 км/ч быстрее 35 км/ч − 28 км/ч = 7 км/ч За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближаться ко второму мотоциклисту на эти 7 километров. Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км 175 − 140 = 35 км Ответ:через 5 часов расстояние между мотоциклистами будет 35 км. Задача 13.Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км? Решение  Найдем скорость сближения: 43 км/ч − 13 км/ч = 30 км/ч Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшаться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км 120 : 30 = 4 ч Значит через 4 часа мотоциклист догонит велосипедиста  На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись. Ответ:мотоциклист догонит велосипедиста через 4 часа. Задача 14.Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально? Решение  Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади: 12 × 0,75 = 9 км/ч — скорость ехавшего впереди Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого: 12 × 6 = 72 км — проехал ехавший сзади 9 × 6 = 54 км — проехал ехавший впереди Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали) 72 км − 54 км = 18 км 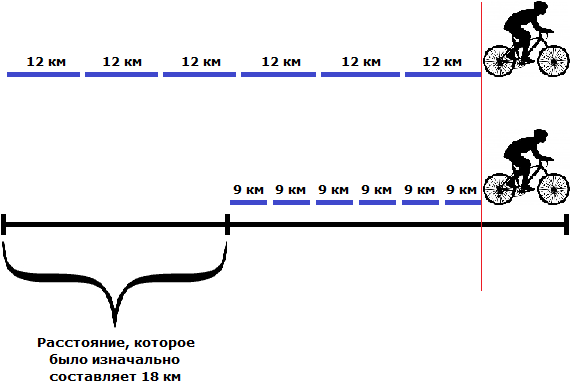 Ответ:между велосипедистами первоначально было 18 км. Задача 15.Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км? Решение  Найдем скорость удаления автомобиля от автобуса 53 км/ч − 41 км/ч = 12 км/ч С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения  Видно, что автомобиль впереди автобуса на 12 км. Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км 48 : 12 = 4 ч  Ответ:через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров. |
