КР по математике. КР по матматике. Задача Заданы функции zf (xy) z(xy) zg(xy). Требуется А) найти б) найти в) показать, что
 Скачать 101.88 Kb. Скачать 101.88 Kb.
|
|
Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта Омский государственный университет путей сообщения Экзаменационное задание (минимум) УРОВЕНЬ МИНИМАЛЬНЫЙ по математике Выполнил студент I курса гр. ____70СЭ-2___ Пластун Владислав Олегович Шифр:____90285_____ Преподаватель Швед Елена Анатольевна 2021 Вариант 73 Задача 1. Заданы функции: z=f (x;y); z=φ(x;y); z=g(x;y). Требуется: А) найти 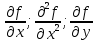 ; ;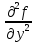 б) найти б) найти 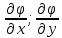 ; в) показать, что ; в) показать, что 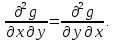 z=f (x;y)=-8-5xy-5x4y2+tg(x2y3); z=φ(x;y)=(1-y)sin(x3-y3) z=g(x;y)=tg(x5-y5). А) 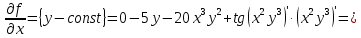 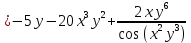 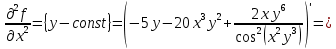  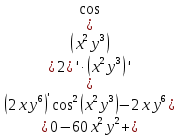 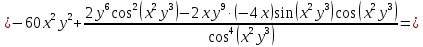 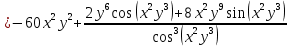 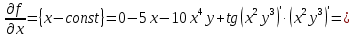 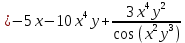 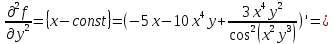  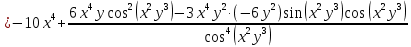 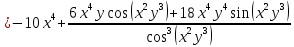 Б) 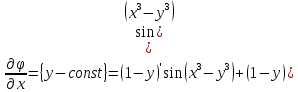 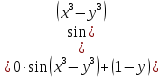  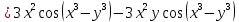  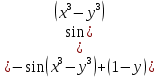   В)  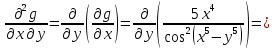 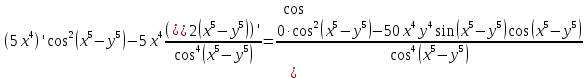   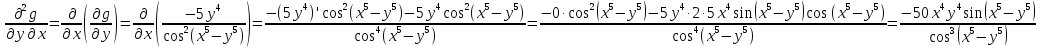 Итак, 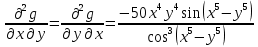 Задача 2. Даны функция z = f(x; y)=-7xy2-4x3-5 и точки А (-7;4), В(-6,8; 3,7). Вычислить: а) точные значения zA = f(xA ; yA ) и B z = f(xB ; yB ); б) полный дифференциал в точке А; в) приближенное значение 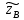 функции f(x; y) в точке В, заменив приращение функции дифференциалом при переходе от точки А к точке В; г) абсолютную и относительную ошибки. функции f(x; y) в точке В, заменив приращение функции дифференциалом при переходе от точки А к точке В; г) абсолютную и относительную ошибки.а) Найдем точные значения функции в точках А и В:  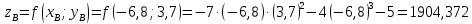 б) Найдем частные производные: 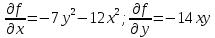 В точке А: 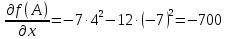  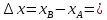 -6,8-(-7)=0,2 – приращение х -6,8-(-7)=0,2 – приращение х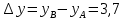 -4=-0,3 – приращение у -4=-0,3 – приращение уПолный дифференциал функции f(x; y) имеет вид: 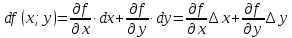  в) 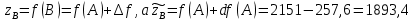 г) абсолютная ошибка:  относительная ошибка: 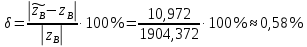 З а д а ч а 3. Найти интегралы методом замены или интегрирования по частям. 1) 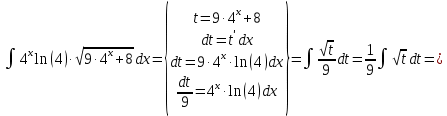  2) 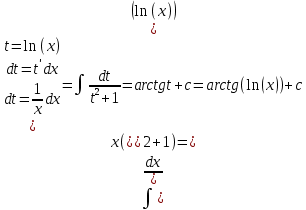 3) 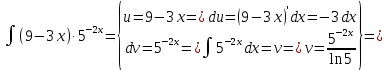 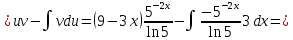  З а д а ч а 4. Найти неопределенный интеграл от рациональной дроби 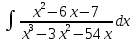 . .Решаем уравнение  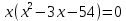 Воспользуемся теоремой Виетта:  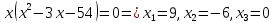 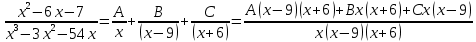  Приравнивая коэффициенты при одинаковых степенях переменной х и свободные члены, получаем систему: 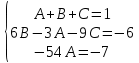 Решаем систему: 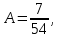 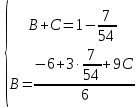 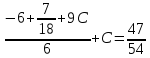 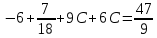  Выполняем проверку: 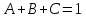 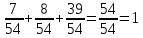 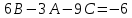 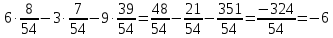   З а д а ч а 5. Найти площадь фигуры, ограниченной заданными линиями 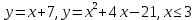 . .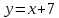  – прямые линии, – прямые линии, 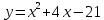 – парабола – параболаНаходим абсциссы точек пересечения параболы с прямой 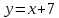 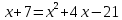 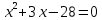 Воспользуемся теоремой Виетта: 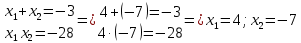 Находим абсциссы точек пересечения параболы с осью Ox: 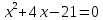 Воспользуемся теоремой Виетта: 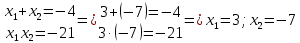 Так как 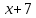 ≥ ≥  на интервале [-7;3], то площадь полученной фигуры вычисляем по формуле: на интервале [-7;3], то площадь полученной фигуры вычисляем по формуле: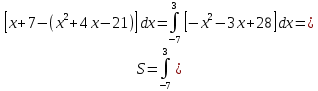 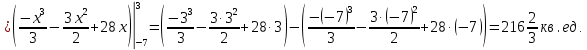 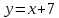 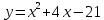
 З а д а ч а 6. Найти общий интеграл дифференциального уравнения 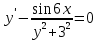 . .Выполним замену и перенесем переменные x и y в разные части уравнения 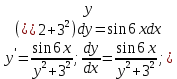 Выполним интегрирование: 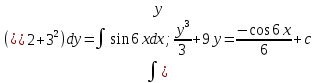 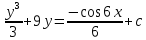 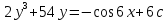  Общее решение:  З а д а ч а 7. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка 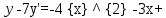 . . Решим его, пользуясь теоремой Виетта: 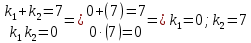 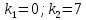 - действительные различные корни - действительные различные корниОбщее решение однородного уравнения:  Правая часть неоднородного уравнения: 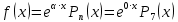 Значит, α=0, n=7, причем  Тогда имеем следующий вид частного решения: Тогда имеем следующий вид частного решения: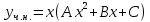 Найдем  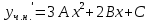 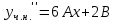 Подставим 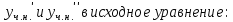 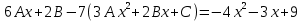    искомое общее решение неоднородного линейного дифференциального уравнения: 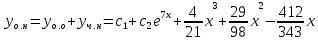 | ||||||||||||||||||||||||||||||||||||
