шпора по егэ информатика. шпора. Задание 1 в любом задании дана таблица. По таблице строим граф. Чтобы легче было построить начинаем с вершину, у которой больше всего вершин или меньше. Задание 13
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
2-3 Задание 1 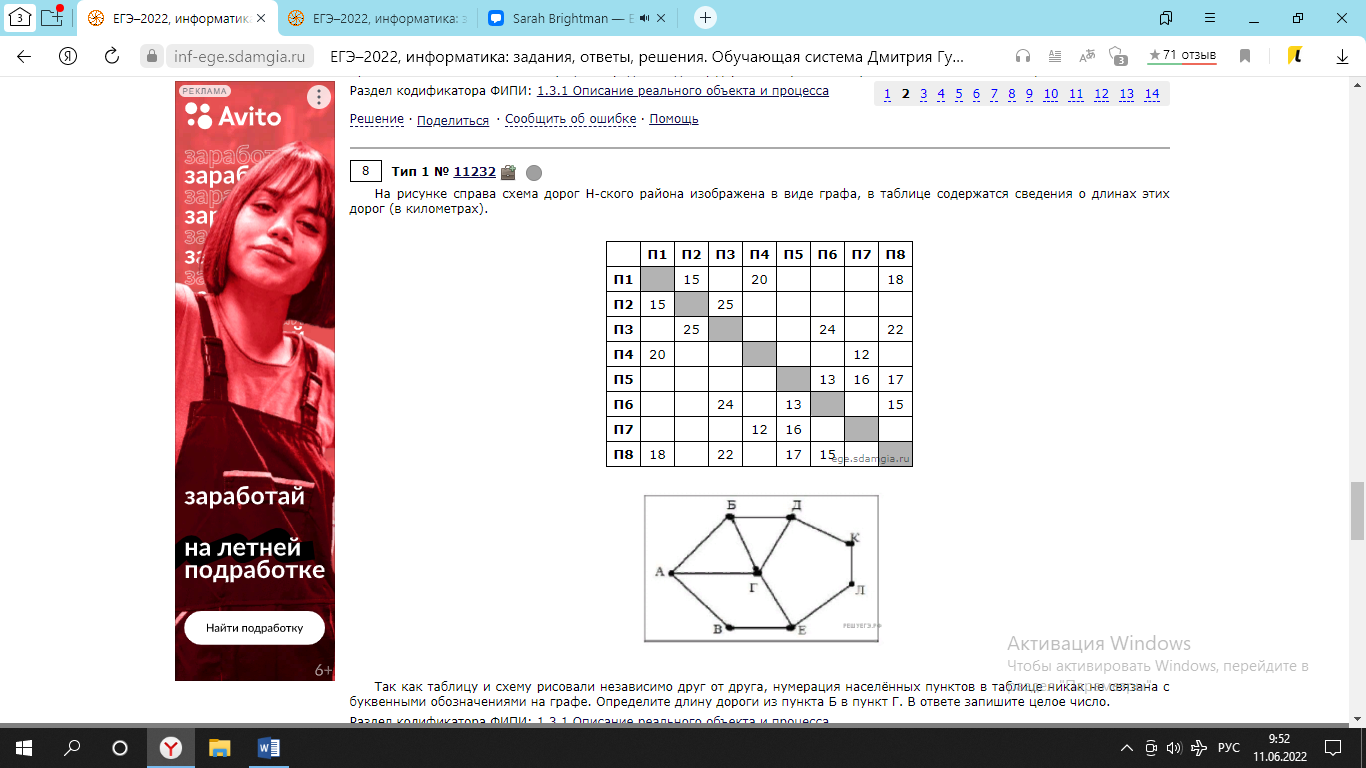 В любом задании дана таблица. По таблице строим граф. Чтобы легче было построить начинаем с вершину, у которой больше всего вершин или меньше. Задание 13  Слева направо считаем количество дорог. В вершинах ставим цифры, полученные сложением всех значений, которые ведут в эту вершину. Если написано, что путь должен проходить только через конкретную вершину, то необходимо зачеркнуть все дороги которые не идут к этому пункту или из него. Если избегая определенную вершину, то зачеркнуть все дороги идущие к ней и из нее 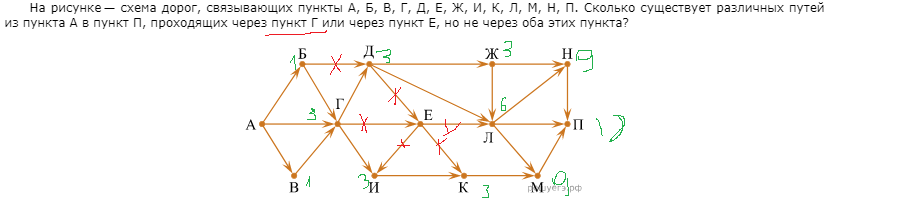 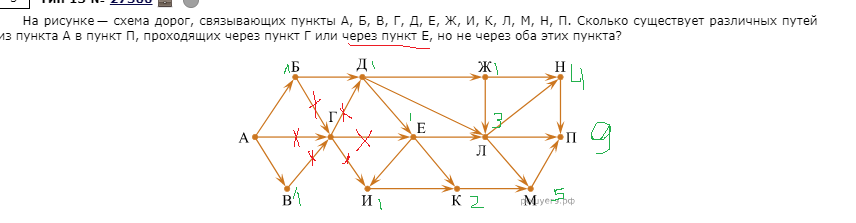 Задание 10 Самые важные кнопки для этого задания ctrl+F. И внимательно прочитать задание. Надо ли учитывать слова в другом падеже или нет. Задание 6 Внимательно перепечатать текст программы и запустить. Задание 16  Если задание дано в виде кода, то перепечатать код и запустить программу. Например, в примере выше надо будет перепечатать код, слово в слово, пробел в пробел, и, дописав print(F(5)) под def запустить код.  В данном случае считаем F(2),F(3),F(4),F(5) – от меньшего к большему. Вторая формула, с n, – это формула в общем случае. Если считаем n = 2: F(2(n = 2)) = F(1(n-1 = 2 – 1))*2(n) = F(1)*2 = 1 * 2 = 2 Не всегда то, что в скобках F, обозначает F(). То есть не всегда F(1) = 1, F(2) = 2, …, F(14) = 14 и т.д. Задание 22.  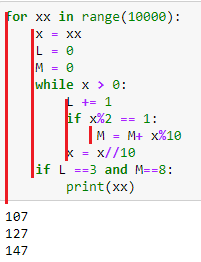 Очень внимательно следим за тем, под какими словами находится print, if, while. Если в задании говорится, что x > 100, то в первой строчке печатаем range(101,10000) Задание 2  Смотрим на данную функцию, считаем переменные. Если их 3, то в таблице будет 8 строчек, если 4 – 16 строк.  Разбиваем выражения на части. Решаем сначала части, потом все выражение  Находи строчки которые представлены в задании в получившийся таблице и сопоставляем переменные. Задание 3 Читаем задание Используя информацию из приведённой базы данных, определите, сколько рублей выручили магазины Октябрьского района от продажи риса (всех видов) за период с 1 по 10 июня включительно. Выделяем ключевую информацию, которую надо будет отсортировать. Открываем таблицу с магазинами и, используя кнопку фильтр оставляем магазины нужного района. Записываем их номера.  Потом в таблице товаров находим весь интересующий нас товар. Записываем его артикул. В таблице движения товаров фильтруем сначала магазины, потом артикул товара, смотрим тип операции – поступление или продажа и сортируем по еще одному признаку. Обязательно Получившуюся таблицу копируем на новый лист. И производим действия. Функция, которая может пригодиться СУММ(). Задание 15  Побитовая конъюнкция Раскрываем конъюнкцию X&25=0 +x&17≠0 + x&A≠0 Переводим числа в двоичную систему 25 – 11001 17 – 10001 По первым двум условиям находим х. отрицаем первыем две переменные и получаем что х и 25 не должно равняться 0, а 17 и х =0 Х - 11**1 – после условия х и 25 Х – 01**0 – после условия х и 17 = 0 Если сказано найти минимум, то вместо * пишем 0. Если макисимум 1. Переводим в десятичную систему. Числовые отрезки вещественные числа - это целые и дробные любого знака раскрываем импликация (стрелочки) и получаем(xA или x2<=100) и(x2>64 или xА) разбираемся с первой скобочкой и неравенством. если х примет значение из отрезка [-10.10] то будет 1 Нужно взять такое отрезок, чтобы выражение х2<=100 было ложным. То есть возвращало 0 значит берем (-беск,-10) и (10,беск)  Теперь перед нами стоит задача выбрать такой отрезок А,чтобы его отрицание закрыло розовые отрезки. Значит А должен быть [-10,10] Аналогично проводим рассуждения для второй части выражения Если x находится в жёлтом диапазоне, причём -8,8 не включается в него, то выражение x2>64 будет истинно. Сейчас стоит задача выбрать такой отрезок А, чтобы закрыть розовый отрезок 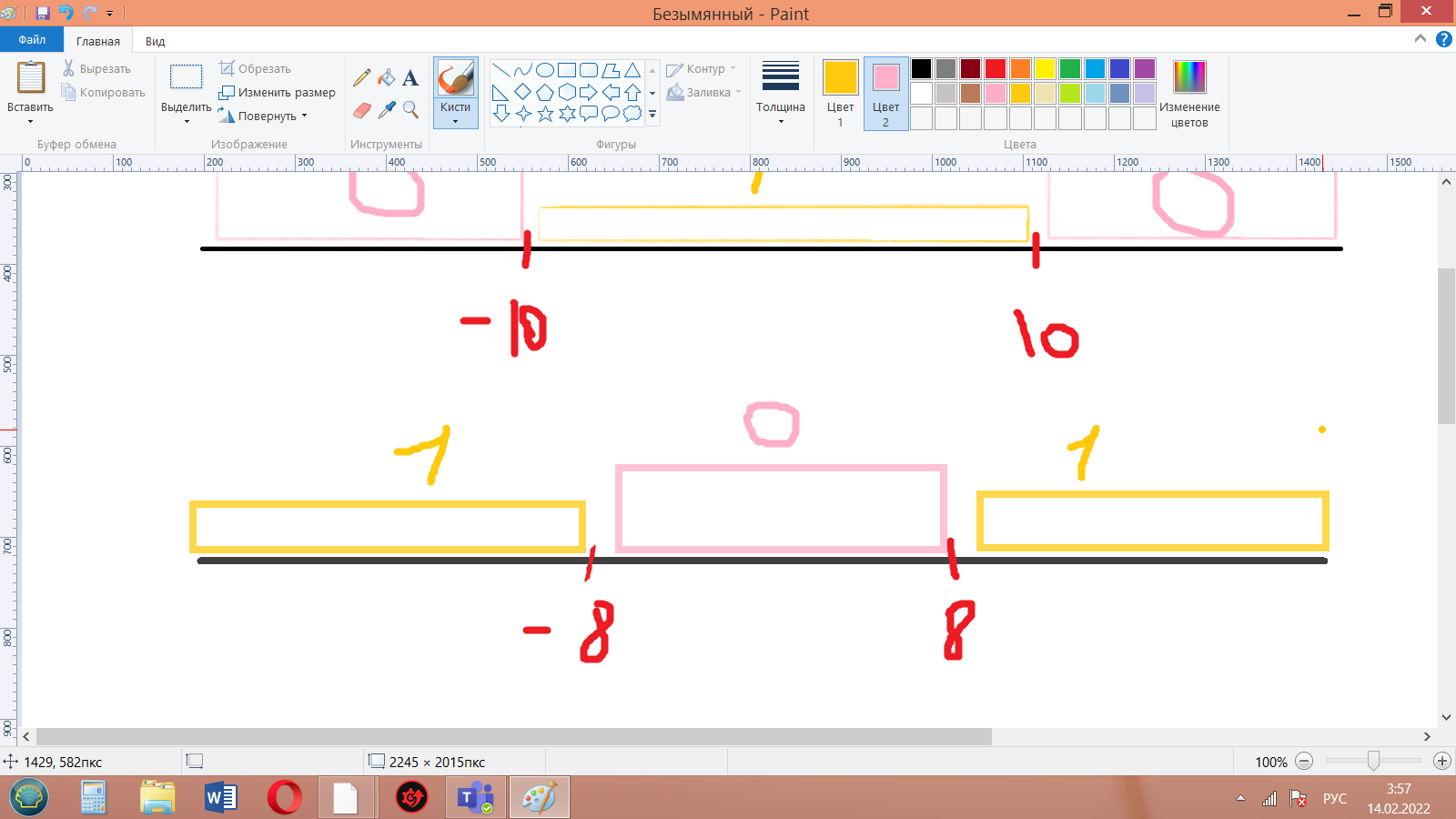 Это будет [-8,8] У нас получилось два отрезка, вопрос задания стоит про наименьшую длину. К значит нам подойдёт второй отрезок, который [-8,8]. Его длина 16. Задание 4 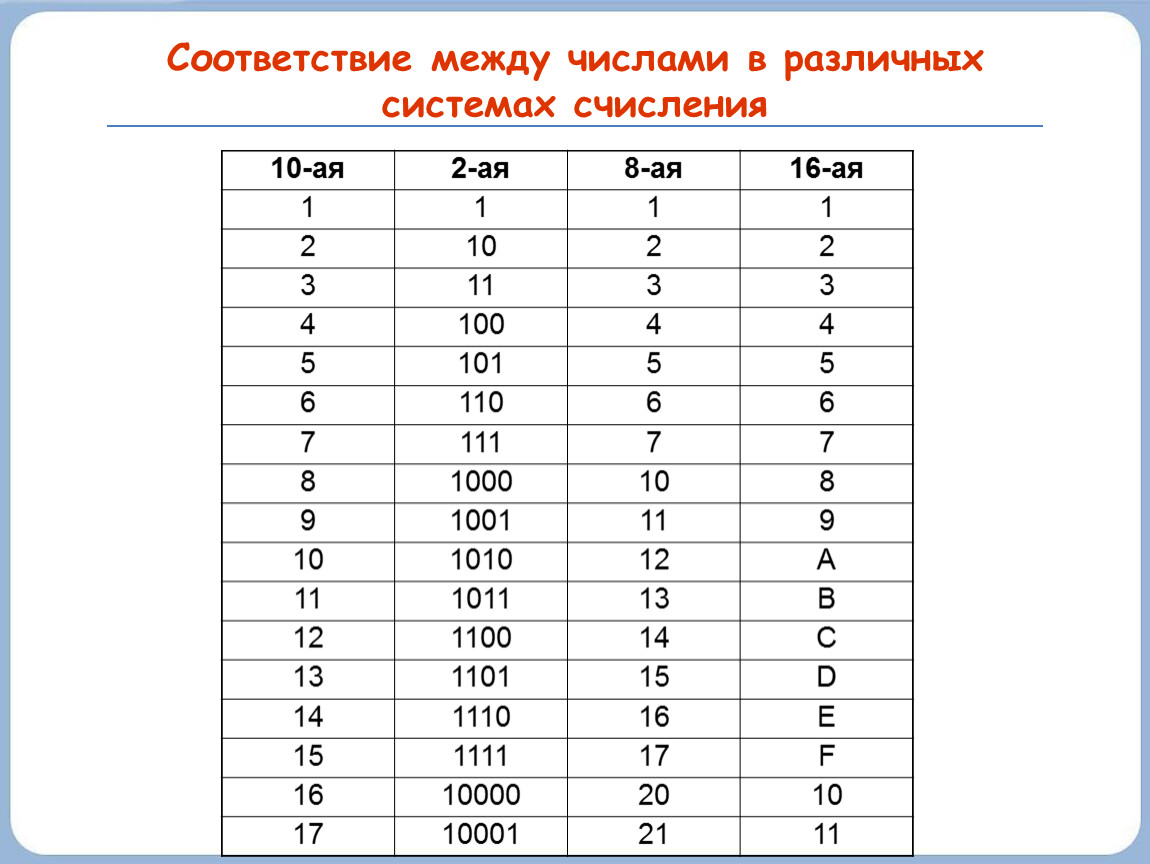 Если задание гласит Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). То 0 – 00 В – 01 Д – 10 П – 11 А – 100 И Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом. Сначала пишем слова, а потом с конца разбиваем по три цифры в случае если нас просят представить 8кодом, и по четыре если 16код Для кодирования букв О, К, Г, Д, Р решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ГОРОДОК таким способом и результат запишите восьмеричным кодом. О – 00 К – 01 Г – 10 Д – 11 Р – 100 0100 0100 0011 0001 42061 8 код 6631 16  Задание на расшифровку сообщений делать внимательно. Там просто смотреть какая буква тут встанет и не появится ли неожиданного кода, который не имеет расшифровки Задания типа Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов? Для этих заданий рисуем дерево.  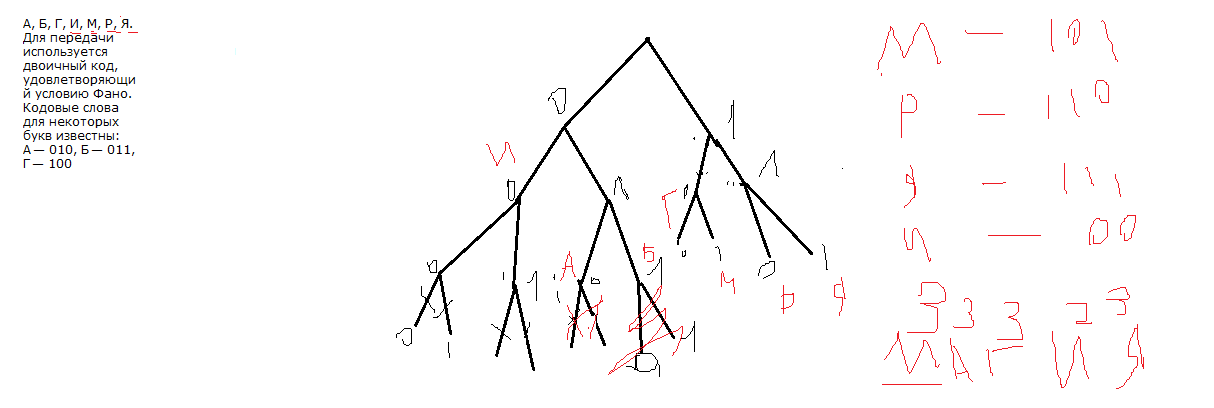 Если в задание дается слово из этих букв, то букву, которая чаще всего встречается в слове кодируем словом наименьшей длины Задание вида По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 00, Г — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ? Как видно не все буквы в искомом слове используются. Дано 7 букв, а используется всего лишь 5. Дерево надо строить для всех букв и используемые в слове буквы пытаться закодировать наименьшей длиной. Задание 7 Надо переводить все в одну систему счисления   Количество битов, кбайт, мбайт не может быть нецелым. Поэтому округляем в большую сторону Звук Количество информации = количество каналов*частота дискритезации*разрешение Стерео – два каналов Моно – один Квадро – четыре 1 кГЦ = 1000 ГЦ Изображение Количество информации = ширина картинки*высота картинки(в пикселях)*кол-во бит для одного цвета. Если цветов используется 30 то надо будет 5 битов Если 3 то 2 бита Если 64 то 6 бит Текст Количество информации = количество символов * кол-во бит для одного цвета Аналогично как и с изображением. Если в алфавите 79 букв то 7 бит и тд. Передача информации время = количество каналов*частота дискритезации*разрешение /скорость передачи = 30 время = количество каналов*частота дискритезации*разрешение*2:1.5 /4*скорость передачи Задача 8 Длина слова – количество звездочек. Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка. и с конца считаем буковки * * * * * е(81) е(27) е(9) е(3) е(1) г(81) г(27) г(9) г(3) г(1) э(81) э(27) э(9) э(3) э(1) и в конце суммируем слева все цифры Вася составляет 4-буквенные слова, в которых могут быть только буквы Ж, И, Р, А, Ф, причём буква Р используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася **** Ж ж ж ж И и и и Р а а а А ф ф ф ф и потом меняет столбики местами и считаем снова. В конце суммируем получившиеся варианты Задание 11 При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, К, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя. Определите объём памяти (в байтах), необходимый для хранения сведений о 50 пользователях. В ответе запишите только целое число — количество байт. Сначала надо закодировать пароль. 12 символов, значит, для кодировки одного символа требуется 5 бит. Пароль состоит из 15 символов. 15*5 =75 бит. Сказано, что пароль хранится в байтах. Значит 75/8 = 9,375, но мы округляем в большую сторону, т.е. 10 байт. 12байт дополнительной информации и 10 байт пароль = 22 байта необходимо для одного пользователя. А для 50 пользователей это будет 50*22 = 1100 байт. некоторой стране автомобильный номер длиной 6 символов составляют из заглавных букв (используются только 33 различных буквы) и десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байтов (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов). Здесь 6 символов это длина номера, а 33 буквы и 10 цифр, итого 43 символа, это то, из чего составляется номер. Для 43 символов потребуется 6 бит, чтобы закодировать 1 символ.(2^6=64. Т.е с помощью 6 бит можно закодировать до 64 символов, а у нас их 43) Задание 5 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу: а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы её цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, которое превышает число 97 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления. Суть задания найти число, которое будет удовлетворять алгоритму. То есть мы берем число, превышающие данное (тут 97, берем 98), переводим в двоичную систему и смотрим подходит ли по условию. Перевод можно сделать вручную или с помощью питона. 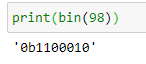 1100010 – это число. И теперь надо удостовериться, что оно подойдет. Начинаем с конца. 0 значит сумма всех цифр в числе была четной. Но если посчитать то получаем 3, а оно не четное и должна там стоять 1 вместо 0. Берем следующее число. 99 оно тоже не подойдет, но не по последней цифре, а по предпоследней. 100,101 не подходят. А 102 подойдет – 1100110. Последний 0 – значит сумма кратна 2, предпоследняя 1 - сумма 1+1+0+0+1 = 3 не кратна 2, значит будет 1. Исполнитель Робот ходит по клеткам бесконечной вертикальной клетчатой доски, переходя по одной из команд вверх, вниз, вправо, влево в соседнюю клетку в указанном направлении. Робот выполнил следующую программу: вверх влево влево вниз вниз вправо вправо вниз вправо вверх Укажите наименьшее возможное число команд в программе, переводящей Робота из той же начальной клетки в ту же конечную. Рисуем на бумаге с клеточками все эти команды. Важно, чтобы робот перемещался или из центра клетки в центр другой клетки или полностью закрашивать клетку. Отмечать начало движения и конец.  Исполнитель Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след в виде прямой линии. У исполнителя существуют следующие команды: Сместиться на вектор (а, b) – исполнитель перемещается в точку, в которую можно попасть из данной, пройдя а единиц по горизонтали и b – по вертикали. Запись: Повторить 5[Команда 1 Команда 2] означает, что последовательность команд в квадратных скобках повторяется 5 раз. Чертежник находится в начале координат. Чертежнику дан для исполнения следующий алгоритм: Сместиться на вектор (5,2) Сместиться на вектор (-3, 3) Повторить 3[Сместиться на вектор (1,0)] Сместиться на вектор (3, 1) На каком расст Здесь надо нарисовать координатную плоскость, поместить чертежника в (0,0) и смешаться на столько, сколько написано 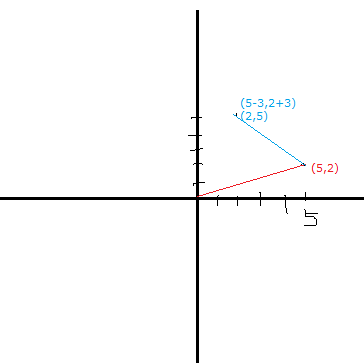 У исполнителя Квадратор две команды, которым присвоены номера: 1. возведи в квадрат, 2. прибавь 1. Первая из них возводит число на экране в квадрат, вторая увеличивает его на 1. Запишите порядок команд в программе, которая преобразует число 2 в число 36 и содержит не более 4 команд. Указывайте лишь номера команд. Здесь мы идет от обратного. То есть мы берем 36 и пытаемся привести к числу 2. Для этого мы извлекаем корень или вынимаем 1. Чтобы извлечь из какого-нибудь числа корень, необходимо чтобы оно было квадратом другого числа. 36 это квадрат 6, 25 квадрат 5, 16 квадрат 4 и тд. 36 ->6 ->5->4->2 Запишем путь обратно 2->4->5->6->36 и через команды 1221 Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам. 1. Складываются первая и вторая, а также вторая и третья цифры исходного числа. 2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей). Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127. Сколько существует чисел, в результате обработки которых автомат выдаст число 1715? Внимательно читаем задание, разбираем пример. Берем данное число и разбиваем его на два, в нашем случае это 17 и 15. И теперь надо найти такие цифры x,y,z, что x+y=17 и y+z=15. или x+y=15 и y+z=17. И перебираем варианты. Важно, чтобы у, как цифра в центре присутствовала в двух суммах. И из этого считаем варианты. Если говорится, найти максимальное число, то ставим на больший разряд максимально возможную цифру из тех, что мы нашли. Задание 12 Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1). Цикл ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным). Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны): НАЧАЛО сместиться на (–1, 2) ПОВТОРИ … РАЗ сместиться на (…, …) сместиться на (–1, –2) КОНЕЦ ПОВТОРИ сместиться на (–24, –12) КОНЕЦ После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?  Исходная точка – (0,0). После выполнения алгоритма он возвращается в (0,0). Х это то, на сколько смещается чертежник относительно оси абсцисс(х), а у относительно оси ординат (у). n количество повторений. Составляется система, где в левой части записаны передвижения чертежника относительно осей координат, а в правой 0, т.к после выполнения он возвращается в начальную точку. С помощью раскрытия скобок необходимо выразить n через х и у. и в получившуюся рассмотрим. Надо чтобы числитель дроби был кратен числителю. Или надо выписать все делители числа сверху. И найти тот, который будет подходить по условию. Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Дана программа для исполнителя Редактор: НАЧАЛО ПОКА нашлось (2222) ИЛИ нашлось (666) ЕСЛИ нашлось (2222) ТО заменить (2222, 6) ИНАЧЕ заменить (666, 2) КОНЕЦ ЕСЛИ КОНЕЦ ПОКА КОНЕЦ Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 239 идущих подряд цифр 6? В ответе запишите полученную строку. Решение на питоне s = '6'*239 # формируем строку из 6. while ('2222' in s) or ('666' in s):дословно «пока нашлось» if '2222' in s: #если нашлось 2222 в строке s = s.replace('2222', '6', 1) #то заменить 2222 на 6 один раз else: s = s.replace('666', '2', 1)#иначе заменить 666 на 2. print(s) #печать получившийся строки В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции. Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся. Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)? НАЧАЛО ПОКА снизу свободно ИЛИ справа свободно ЕСЛИ снизу свободно ТО вниз ИНАЧЕ вправо КОНЕЦ ЕСЛИ КОНЕЦ ПОКА КОНЕЦ  Здесь перерисовываем карту, стены и тд. И ставим исполнителя в каждую клетку и проходим по алгоритму. Клетка финиша также учитывается при подсчете. Важно учитывать какая команда ЕСЛИ стоит сначала.  Задание 14 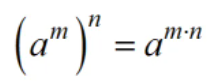 Числовой ряд в 10 сс: 0,1,2,3,4,5,6,7,8,9,10… В 2 сс: 0,1,10,11,100,101,110,111,1000… В 3 сс: 0,1,2,10,11,12,20,21,22,100… В 4 сс: 0,1,2,3,10,11,12,13,20,21,22,23,30,31,32,33,100.. И тд 4 = 22 в десятичной сс, а в двоичной 100 То есть показатель степени отвечает за количество нулей Если 54 в десятичной, то в сс с основанием 5 это будет иметь следующий вид 1000 Значение арифметического выражения: 918 + 354 – 17 — записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи? По свойствам показателей степени приводим к одному основанию 918=(32)18=336 Значит будет 1 и 54 нуля, где на вместо 37 нуля справа будет 1. Переводим 17 вручную 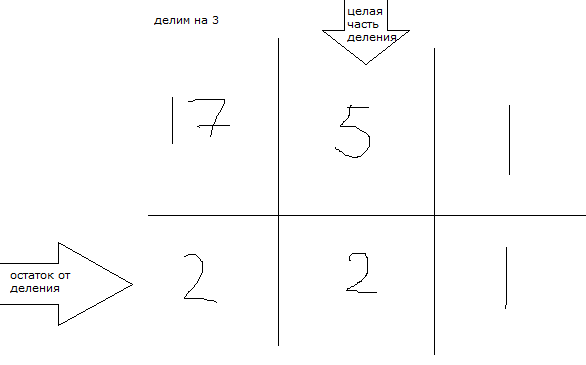 Когда целая часть становится меньше делителя, то деление прекращается. Результат записывается справа налево, то есть 17 в десятичной, но в сс с основание 3 это будет 221  Из 36 цифр два нуля, а остальные двойки, значит 36-2 = 34 Задание 18 Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Задание 18 Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Копируем таблицу и размещаем ее ниже, выделив внешними границами. Удаляем в новой таблице цифры 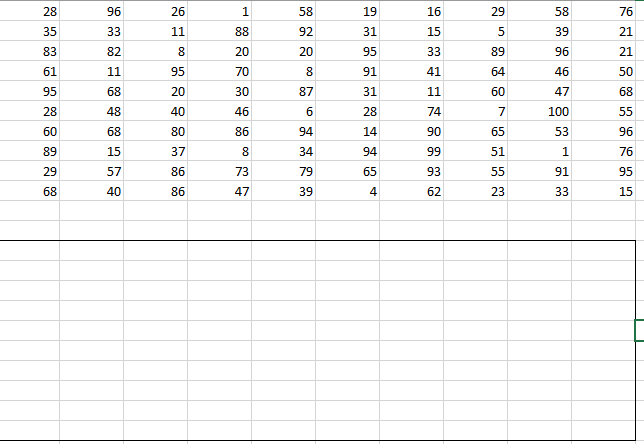 Внимательно читаем, откуда и куда будет двигаться робот. В первую клетку ставим количество монет, которые в оригинальной таблице через строку формул  в граничные ячейки необходимо занести сумму из предыдушей клетки новой таблицы и из соответствующей ячейки оригинальной таблицы 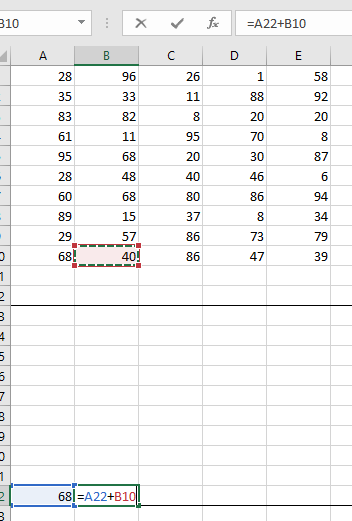 В ячейку по диагонали от стартовой необходимо записать максимальную сумму  Протянуть формулу на оставшуюся часть поля. Это будет максимум. Для поиска минимума необходимо ctrl+F, вкладка заменить, кнопка заменить все 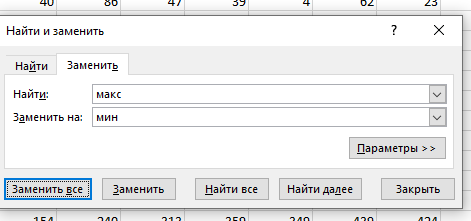 Задание 9 Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений максимальная суточная температура оказывалась выше среднесуточной на 7 и более градусов. Сначала читаем внимательно задание и разбиваем его на части Сначала находим среднесуточную температуру в отдельном столбике  В следующем столбике находим максимальное за сутки  А потом находим разницу между максимумом и среднем значением  А потом считаем, если больше 7 градусов  Задание 19 Берем количество камней, которое необходимо для победы и делим на то число, во сколько раз можно увеличить камней в кучке. Необходимо, чтобы количество камней делилось дважды без остатка. Пример, необходимо 58 камней для победы. Можно в кучку добавлять 1 камень или увеличивать количество камней в 3 раза. 58:3 =29,33. Не подходит. 60:3 = 20. Но 20 если снова разделить на 3 не поделится ровно. 63:3 = 21. 21:3 = 7. 7 ответ Задание 20 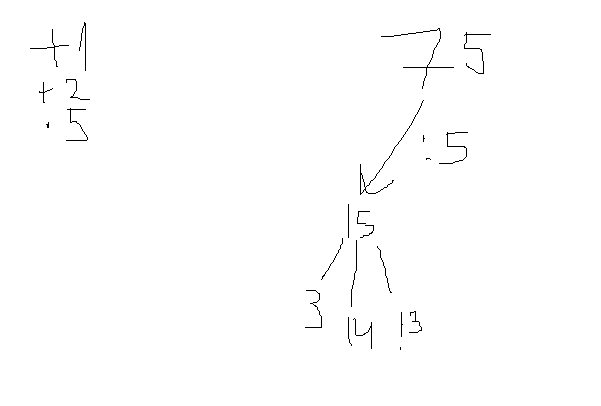 Если одна кучка, то сначала делим количество камней для победы. И округляем в меньшую сторону. Если разделилось ровно, то вычитаем 1. И вычитаем количество камней, которые можно добавлять в кучку. Если две кучки то из необходимого для победы количества камней вычитаем количество камней в данной кучке. С получившимся числом проделываем тоже самое, что и с одной кучкой, только вычитаем 1 раз. Рассматриваем второй вариант развития событий. Увеличиваем количество камней в известной кучке в то количество раз, в какое можно. Вычитаем из необходимых камней количество камней в увеличенной кучке. Делим получившиеся камни и округляем вниз. Задание 21 Если в прошлом задании получилось два числа, то из минимального вычитаем 1 Если три, то из среднего вычитаем 1 Но может быть не 1, а другое минимальное количество камней, которые можно добавить в кучку |
